



suivant: 6. Déduction naturelle au
monter: II. Logique du premier
précédent: 4. Logique du premier
Table des matières
Index
Sous-sections
Il est important de préciser que la logique du
premier ordre est indécidable, cela signifie qu'il n'existe
pas d'algorithme pour déterminer si une formule est valide ou
non valide. Ce résultat fut établi par Alonzo
Church et Alan
Türing en 1936 et
1937 [4,24]. Ils ont aussi montré que
cette logique est semi-décidable, c'est-à-dire que nous
pouvons écrire un programme, qui prend en entrée une formule et
qui a le comportement suivant :
- S'il termine alors il décide correctement si la formule est
valide ou non. Lorsque la formule est valide, la décision est
généralement accompagnée d'une preuve.
- Si la formule est valide, alors il termine. Cependant,
l'exécution peut être longue !
Notons que si la formule n'est pas valide, la terminaison de ce
programme n'est pas garantie.
En effet si le programme terminait pour toute formule, alors, d'après le
premier point, ce serait un algorithme pour déterminer si une formule est
valide ou non. Or, ainsi qu'il est dit ci-dessus, Church et Türing ont
prouvé qu'un tel algorithme n'existait pas.
Plan : Dans ce chapitre nous commençons par
présenter de méthodes introduites par Jacques
Herbrand, permettant
d'énumérer un ensemble fini de formules afin de trouver un
modèle à une formule. Ensuite nous présentons la transformation
due à Thoralf Albert Skolem qui transforme (skolémise) une formule
en une «forme de Skolem » où l'existence d'un modèle est
préservée. En transformant ensuite cette forme de Skolem en une
«forme clausale » équivalente, nous pouvons appliquer la
résolution. Nous reprenons alors le concept de résolution
introduit dans le chapitre 2 et nous l'étudions en
logique du premier ordre. En 1929, Kurt Gödel (1906 - 1978)
prouva que la logique du premier ordre est complète et
cohérente. Nous présentons ce résultat pour la résolution,
c'est-à-dire qu'il existe une preuve par résolution en logique du
premier ordre d'une formule F à partir d'un ensemble de formules
Γ si et seulement si F est conséquence de Γ.
Jacques Herbrand (1908-1931) est un mathématicien et logicien
français. Il a établi en 1930 un lien entre calcul des prédicats et
calcul des propositions.
Nous introduisons d'abord la notion de fermeture universelle qui
permet de transformer toute formule en une formule fermée où la
propriété de satisfiabilité est maintenue.
Définition 5.1.1 (Fermeture
universelle)
Soit C une formule ayant pour variables libres
x1,…, xn.
La fermeture universelle de C, notée
∀(C), est la
formule
∀x1…∀xnC. Cette notion est
définie à l'ordre près des variables libres de C. Soit Γ
un ensemble de formules,
∀(Γ) = {∀(A) | A∈Γ}.
Nous généralisons la définition 1.3.1 aux termes de la logique
du premier ordre.
Définition 5.1.3 (Substitution)
Une substitution est une application des variables dans les termes.
Soient A une formule et σ une substitution. Aσ est la
formule obtenue en remplaçant toute occurrence libre d'une variable
par son image dans l'application. La formule Aσ est une
instance de A.
Dans la suite de ce chapitre, nous ne considérons que des formules qui ne contiennent
ni le symbole égal, ni les constantes propositionnelles
 ,
, , car leur sens est fixé dans toute
interprétation :
, car leur sens est fixé dans toute
interprétation :  vaut 1,
vaut 1,  vaut 0, et le symbole = est l'identité sur le
domaine de l'interprétation (voir Remarque 4.3.18).
De plus nous considérons que toute signature comporte
au moins une constante. Ainsi la signature d'un ensemble de formules
ne comportant pas de constante, sera arbitrairement complétée par la
constante a.
vaut 0, et le symbole = est l'identité sur le
domaine de l'interprétation (voir Remarque 4.3.18).
De plus nous considérons que toute signature comporte
au moins une constante. Ainsi la signature d'un ensemble de formules
ne comportant pas de constante, sera arbitrairement complétée par la
constante a.
Définition 5.1.4 (Domaine et base de Herbrand)
- Le domaine de Herbrand pour
Σ est l'ensemble des termes fermés (i.e., sans
variable) de cette signature, dénoté par DΣ.
- La base de Herbrand pour Σ
est l'ensemble des formules atomiques fermées de cette signature, nous la notons BΣ.
Notons que le domaine de Herbrand d'une signature sans constante est
vide. Puisque toutes les signatures considérées dans ce chapitre
doivent comporter au moins une constante, ce domaine
n'est pas vide.
Exemple 5.1.5
Calculs de base de Herbrand :
- Soit Σ la signature comportant uniquement les 2 constantes a, b et les 2 symboles de relations unaires P, Q. Nous avons
DΣ = {a, b} et
BΣ =
- Soit Σ la signature comportant uniquement la constante a, le
symbole de fonction unaire f et le symbole de relation unaire
P. Nous avons
DΣ = {fn(a) | n∈
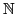 } et
BΣ =
} et
BΣ =
À partir de la base et du domaine de Herbrand d'une formule, nous
sommes capables de construire une interprétation dite de «Herbrand ».
Définition 5.1.6 (Interprétation de Herbrand)
Soient Σ une signature et
E⊆BΣ. L'interprétation de Herbrand
HΣ, E a
pour domaine DΣ et donne aux symboles le sens suivant :
- Si le symbole s est une constante de la signature, il vaut lui-même dans cette interprétation.
- Si s est un symbole de fonction à n≥1 arguments de la
signature et si
t1,..., tn∈DΣ alors
sfnHΣ, E(t1,..., tn) = s(t1,..., tn).
- Si le symbole s est une variable propositionnelle, il vaut
1, autrement dit il est vrai, si et seulement si s∈E.
- Si s est un symbole de relation de la signature à n≥1
arguments et si
t1,..., tn∈DΣ
alors
srnHΣ, E = {(t1,..., tn) | t1,..., tn∈DΣ∧s(t1,..., tn)∈E}.
Le résultat suivant montre qu'une interprétation de Herbrand peut être
identifiée à l'ensemble des formules atomiques fermées dont elle est
modèle.
Propriété 5.1.7 (Propriété d'une interprétation de Herbrand)
Soient Σ une signature et
E⊆BΣ. Dans
l'interprétation de Herbrand
HΣ, E :
- La valeur d'un terme sans variable est lui-même.
- L'interprétation est modèle d'une formule atomique fermée
si et seulement si elle est élément de E.
La preuve est une conséquence directe de la définition d'une interprétation de
Herbrand.
Notons ici, avec un exemple, pourquoi on a supposé que les formules ne contiennent pas
les symboles de relation
 ,
, , =, dont le sens est fixé dans toutes les interprétations.
Supposons au contraire que
, =, dont le sens est fixé dans toutes les interprétations.
Supposons au contraire que  soit élément de la base mais non élément de E.
D'après le point 2, l'interprétation
HΣ, E donnerait
soit élément de la base mais non élément de E.
D'après le point 2, l'interprétation
HΣ, E donnerait  la valeur 0, alors que
la valeur 0, alors que
 vaut 1 dans toute interprétation.
vaut 1 dans toute interprétation.
Exemple 5.1.8
Soit Σ la signature comportant les 2 constantes a, b et les
2 symboles de relations unaires P, Q. L'ensemble
E = {P(b), Q(a)} définit l'interprétation de Herbrand
HΣ, E de domaine
Lemme 5.1.9
Soit I une interprétation de la signature Σ. Soit A une formule
sur cette signature.
L'interprétation I est modèle de
∀(A) si et seulement si
pour tout état e de cette l'interprétation, l'assignation (I, e) est modèle de A.
Preuve : Ce lemme est une conséquence directe du sens de ∀. Soit
x1,…, xn une liste des variables libres de A. Nous
rappelons que
∀(A) = ∀x1…∀xnA.
- Supposons que l'interprétation I est modèle de
∀(A). Montrons que pour tout état e, l'assignation
(I, e) est modèle de A. Soit e un état quelconque. Nous
prouvons, par récurrence sur i que (I, e) est modèle de
∀xi…∀xnA.
- Cas i = 1. I étant modèle de la formule fermée
∀(A), alors pour tout état e, (I, e) est modèle de
∀(A), ce qui établit la propriété pour i = 1.
- Supposons que (I, e) est modèle de
∀xi…∀xnA. Montrons que (I, e) est modèle de
∀xi+1…∀xnA.
D'après l'hypothèse de récurrence ci-dessus et le sens de
∀, pour tout état f différent de e au plus par la
valeur de xi, (I, f ) est modèle de
∀xi+1…∀xnA. Puisque e est un tel état, (I, e) est modèle
de
∀xi+1…∀xnA.
En appliquant la propriété établie ci-dessus pour tout i≥1 au
cas où i = n + 1, nous avons (I, e) modèle de
∀xn+1…∀xnA, autrement dit (I, e) est modèle de A.
- Supposons que pour tout état e, l'assignation (I, e) est modèle de A.
Nous prouvons, par récurrence sur i, que, pour tout état e,
(I, e) est modèle de
∀xn+1-i…∀xnA.
- Cas i = 0. Puisque
∀xn+1…∀xn = A,
par hypothèse, la propriété est vérifiée pour i = 0.
- Supposons que pour tout état e, (I, e) est modèle de
∀xn+1-i…∀xnA. Montrons que pour tout état e,
(I, e) est modèle de
∀xn+1-(i+1)…∀xnA.
Notons que
n + 1 - (i + 1) = n - i.
Soit e un état quelconque. D'après le sens de
∀, (I, e) est modèle de
∀xn-i…∀xnA si et seulement si, pour tout état f différent de e
au plus par la valeur de xn-i, (I, f ) modèle de
∀xn+1-i…∀xnA. Par hypothèse de récurrence,
cette dernière propriété est vérifiée. Donc, puisque
l'état e est quelconque, pour tout état g, (I, g) est
modèle de
∀xn-i…∀xnA.
En appliquant la propriété établie ci-dessus pour tout i, au cas où
i = n, nous avons : pour tout état e, (I, e) est modèle de
∀(A). Puisque cette formule est sans variable libre, sa valeur
ne dépend pas de l'état e, donc I est modèle de
∀(A).

Lemme 5.1.10
Soit A une formule sans quantificateur sur la signature Σ.
Soit σ une substitution pour cette signature, autrement dit une application
des variables dans les termes sur cette signature. Soit I une interprétation
de la signature Σ et e un état de cette interprétation.
Nous avons :
[Aσ](I, e) = [A](I, f) où pour toute variable x,
f (x) = [[σ(x)]](I, e),
autrement dit f (x) est la valeur du terme σ(x) dans l'assignation (I, e).
Preuve : La preuve de ce lemme est longue et sans intérêt, c'est pourquoi
nous l'avons omise. En fait, elle consiste à prouver par récurence
les deux faits suivants :
- Pour tout terme t,
[[tσ]](I, e) = [[t]](I, f).
- Pour toute formule A sans quantificateur,
[Aσ](I, e) = [A](I, f).

Lemme 5.1.11
Soit A une formule sans quantificateur sur la signature
Σ. Soit I une interprétation de cette signature. Si I est
modèle de
∀(A), alors, pour tout état e, l'assignation
(I, e) est modèle de toute instance de A.
Preuve : Soit B une instance de A sur Σ. Par définition des
instances, il existe une substitution σ sur la signature
Σ, telle que
B = Aσ. Soient e un état
quelconque et f l'état où pour toute variable x,
f (x) est la valeur du terme σ(x) dans l'assignation
(i, e). Supposons que I est modèle de
∀(A). D'après le
lemme 5.1.9, (I, f ) est modèle de A.
D'après le lemme 5.1.10 (I, e) est modèle de
B.
Lemme 5.1.12
Soit A une formule sans quantificateur ni variable sur la
signature Σ. Soit I une interprétation de cette signature,
qui est modèle de A. Soit E l'ensemble des éléments de
BΣ, la base de Herbrand pour Σ, dont I est
modèle. L'interprétation de Herbrand
HΣ, E est modèle de
A.
Preuve : Nous faisons la preuve par récurrence sur le nombre de connecteurs
de A. Supposons que pour toute formule A sans
quantificateur ni variable sur la signature Σ ayant moins
de n connecteurs, l'interprétation de Herbrand
HΣ, E
est modèle de A.
Soit la formule A sans quantificateur
ni variable sur la signature Σ, ayant I comme modèle
avec n connecteurs.
- Supposons n = 0. Alors A est dans la base de Herbrand pour
Σ. Puisque I est modèle de A, par définition de E,
nous avons A∈E. Et d'après la propriété 5.1.7,
HΣ, E est modèle de A.
- Supposons n > 0. Alors A est de l'une des formes
¬B,(B∧C),(B∨C),(B⇒C),(B⇔C) où B et C sont des formules avec moins de n
connecteurs. Nous n'examinons que le cas
A = (B∧C), car
les autres cas sont analogues. Puisque I est modèle de A,
alors I est modèle de B et de C. Par hypothèse de
récurrence,
HΣ, E est modèle de B et de C, donc
aussi modèle de A.

Définition 5.1.13 (Assignation propositionnelle caractéristique)
Soit Σ une signature. Soit E un sous-ensemble de
BΣ la base de Herbrand pour Σ. L'assignation
propositionnelle de domaine
BΣ caractéristique de
E est l'application
v : BΣ→{0, 1} qui vérifie pour tout
A∈BΣ, v(A) = 1 si et seulement si A∈E.
Lemme 5.1.14
Soit A une formule sans quantificateur ni variable sur la
signature Σ. Soit E un sous-ensemble de
BΣ la
base de Herbrand pour Σ. Soit v l'assignation
propositionnelle de domaine
BΣ caractéristique de
E.
L'interprétation de Herbrand
HΣ, E est modèle du
premier ordre de A si et seulement si v est modèle
propositionnel de A.
Preuve : La preuve est analogue à la précédente, par récurrence sur le
nombre de connecteurs de A. Aussi nous ne traitons que le cas où
A ne comporte aucun connecteur. La formule A est alors
élément de la base de Herbrand pour Σ.
D'après la
propriété 5.1.7,
HΣ, E est modèle de A
si et seulement si A∈E. Par définition de v, A∈E si et
seulement si v(A) = 1. Donc
HΣ, E est modèle de A si
et seulement si v est modèle de A.
Soit e un état de l'interprétation de Herbrand
HΣ, E. Par
définition d'une telle interprétation, pour toute variable x, e(x)
est un élément de
DΣ l'ensemble des termes fermés sur la
signature Σ. L'état e est aussi une substitution pour
Σ. Ainsi, nous pouvons appliquer la substitution e à toute
formule A sur la signature Σ. Nous rappelons qu'appliquer la
substitution e à la formule A est notée Ae.
Lemme 5.1.15
Soit e un état de l'interprétation de Herbrand
HΣ, E.
Soit A une formule sans quantificateur sur Σ.
L'interprétation
HΣ, E est modèle de Ae si et seulement si
l'assignation
(HΣ, E, e) est modèle de A.
Preuve : Soit f un état quelconque de
HΣ, E.
D'après le lemme
5.1.10, l'assignation
(HΣ, E, f ) est
modèle de Ae si et seulement si l'assignation
(HΣ, E, g)
est modèle de A où, pour toute variable x, g(x) est la
valeur de e(x) dans l'assignation
(HΣ, E, f ). Puisque Ae
est une formule sans variable, l'assignation
(HΣ, E, f ) est
modèle de Ae si et seulement si l'interprétation
HΣ, E
est modèle de Ae. Pour toute variable x, e(x) est un terme
sans variable. Donc, d'après la propriété 5.1.7, la
valeur de e(x) dans une assignation de Herbrand est e(x) et par
suite g = e. Par suite l'interprétation
HΣ, E est
modèle de Ae si et seulement si l'assignation
(HΣ, E, e)
est modèle de A.
Théorème 5.1.16 (Fermeture universelle et modèle de Herbrand)
Soit Γ un ensemble de formules sans quantificateur sur la
signature Σ. La fermeture universelle
∀(Γ) a un
modèle si et seulement si
∀(Γ) a un modèle qui est une
interprétation de Herbrand de Σ.
Preuve : L'implication de droite à gauche est trivial. Prouvons
l'implication de gauche à droite. Soit I une interprétation de
Σ, qui est modèle de
∀(Γ). Soit E l'ensemble
des éléments de
BΣ, dont I est modèle.
Nous montrons que l'interprétation de Herbrand
HΣ, E est
modèle
∀(Γ). Soit A une formule quelconque de
Γ. Puisque
A∈Γ, I est modèle de
∀(A).
Soit e un état quelconque de
HΣ, E. D'après le lemme
5.1.11 et le fait que Ae est une formule sans
quantificateur ni variable, I est modèle de Ae. D'après le
lemme 5.1.12,
HΣ, E est
aussi modèle de Ae. D'après le lemme
5.1.15, l'assignation
(HΣ, E, e)
est modèle de A. Puisque e est un état quelconque de
HΣ, E, d'après le lemme 5.1.9,
l'interprétation de Herbrand
HΣ, E est modèle de
∀(A). Puisque A est une formule quelconque de Γ,
HΣ, E est modèle de
∀(Γ).
Ce théorème est appliqué dans la preuve du
théorème 5.2.17.
Le théorème de Herbrand établit un lien entre la logique du premier
ordre et la logique propositionnelle.
Théorème 5.1.17 (Théorème de Herbrand)
Soit Γ un ensemble de formules sans quantificateur de
signature Σ.
∀(Γ) a un modèle si et seulement si tout
ensemble fini d'instances fermées sur la signature Σ des
formules de Γ a un modèle propositionnel application de la
base de Herbrand BΣ dans l'ensemble {0, 1}.
Preuve :
-
⇒
- Supposons que
∀(Γ) a un modèle
I, qui est une interprétation de Σ. Soit E l'ensemble
des éléments de BΣ, dont I est modèle. Soit v
l'assignation propositionnelle de domaine
BΣ
caractéristique de E. Nous montrons que v est un modèle
propositionnel des instances fermées des formules de
Γ. Soit A une telle instance. D'après le lemme
5.1.11, I est modèle de A. D'après le lemme
5.1.12, l'interprétation de
Herbrand
HΣ, E est modèle de A. D'après le lemme
5.1.14, v est modèle de A.
-
⇐
- Supposons que tout ensemble fini
d'instances fermées sur la signature Σ des formules de
Γ a un modèle propositionnel de domaine BΣ.
D'après le théorème de compacité
(théorème 1.2.30) l'ensemble de toutes les
instances fermées sur la signature Σ a alors un modèle
propositionnel v de domaine BΣ. Ce modèle propositionnel
peut être vu comme le modèle de Herbrand de
∀(Γ)
associé à l'ensemble des éléments de la base de Herbrand
dont v est modèle. En effet, soit
E = {A∈BΣ | v(A) = 1}. Soit A une formule quelconque de Γ.
D'après le lemme 5.1.14,
l'interprétation de Herbrand
HΣ, E est modèle des
instances fermées de A, autrement dit, pour tout état e de
cette interprétation,
HΣ, E est modèle de
Ae. D'après le lemme 5.1.15, pour
tout e, l'assignation
(HΣ, E, e) est modèle de
A. D'après le lemme 5.1.9,
l'interprétation
HΣ, E est modèle de
∀(A). Puisque A est une formule quelconque de Γ,
cette interprétation est modèle de
∀(Γ).

Corollaire 5.1.18
Soit Γ un ensemble de formules sans quantificateur de signature
Σ. La fermeture universelle
∀(Γ) est
insatisfaisable si et seulement s'il existe un ensemble fini
insatisfaisable d'instances fermées sur la signature Σ des
formules de Γ.
Preuve : Le corollaire est obtenu en remplaçant chaque côté de l'équivalence
du théorème de Herbrand par sa négation.
Dans le cas où Γ est un ensemble fini de formules, ce
corollaire fonde une procédure de semi-décision pour savoir si
∀(Γ) est ou n'est pas insatisfaisable : nous énumérons
l'ensemble des instances fermées des formules de Γ sur la
signature Σ et nous arrêtons cette énumération dès que nous
obtenons un ensemble insatisfaisable, ou dès que cette énumération est
terminée sans contradiction ou dès que nous sommes «fatigués » :
- Dans le premier cas, la procédure répond (en appliquant le
corollaire) que
∀(Γ) est insatisfaisable.
- Le deuxième cas ne peut se produire que si le domaine de
Herbrand ne comprend que des constantes, la procédure répond (en
appliquant le corollaire) que
∀(Γ) est satisfaisable et
en donne un modèle.
- Dans le troisième cas, nous ne pouvons évidemment pas conclure :
le corollaire nous dit que si
∀(Γ) est insatisfaisable,
et si nous avions été plus courageux, nous aurions obtenu une
contradiction.
Exemple 5.1.19
- Soit
Γ = {P(x), Q(x),¬P(a)∨¬Q(b)}. La
signature Σ comporte 2 constantes a, b et 2 symboles de
relation unaire P, Q.
- Soit
Γ = {P(x)∨Q(x),¬P(a),¬Q(b)}. Nous avons
la même signature que précédemment.
- Soit
Γ = {P(x),¬P(f (x))}. La signature Σ comporte
une constante a, un symbole de fonction unaire f et un symbole de
relation unaire P. La constante a est ajoutée à la signature de
Γ pour que le domaine de Herbrand ne soit pas vide.
- Soit
Γ = {P(x)∨¬P(f (x)),¬P(a), P(f (f (a)))}.
Nous avons la même signature que précédemment.
- Soit
Γ = {R(x, s(x)), R(x, y)∧R(y, z)⇒R(x, z),¬R(x, x)}. La signature Σ comporte
une constante a, un symbole de fonction unaire s et un symbole
de relation binaire R.
Le théorème de Herbrand est applicable à la fermeture universelle d'un
ensemble de formules sans quantificateur. Nous étudions une
transformation, la skolémisation, qui
change un ensemble de formules fermées en la fermeture universelle
d'un ensemble de formules sans quantificateur et qui préserve
l'existence d'un modèle. Cette transformation est due à Thoralf
Albert Skolem (1887 - 1963),
mathématicien et logicien norvégien. Elle est nécessaire pour pouvoir
appliquer la résolution sur un ensemble de formules de la logique du
premier ordre. Nous commençons par donner l'intuition de la
skolémisation avant de regarder le résultat de cette transformation
sur des exemples simples afin d'observer les propriétés de la
skolémisation. La skolémisation sert à éliminer les quantificateurs
existentiels et change une formule fermée A en une formule B telle
que :
- B a pour conséquence A.
- tout modèle de A donne un modèle de B.
Par suite A a un modèle si et seulement si B a un modèle : la
skolémisation préserve l'existence d'un modèle, nous disons aussi
qu'elle préserve la satisfaisabilité. Regardons ce qu'il en est sur
deux exemples simples.
Exemple 5.2.1
La formule
∃xP(x) est skolémisée en P(a). Nous
observons les relations entre ces deux formules :
- P(a) a pour conséquence
∃xP(x).
-
∃xP(x) n'a pas pour conséquence P(a) mais un modèle
de
∃x P(x) «donne » un modèle de P(a). En effet soit
I un modèle de
∃xP(x). Donc il existe
d∈PI. Soit J l'interprétation telle que PJ = PI et aJ = d. J est modèle de P(a).
Exemple 5.2.2
La formule
∀x∃yQ(x, y) est skolémisée en
∀xQ(x, f (x)). Nous observons les relations entre ces deux
formules :
-
∀xQ(x, f (x)) a pour conséquence
∀x∃yQ(x, y).
-
∀x∃yQ(x, y) n'a pas pour conséquence
∀xQ(x, f (x)) mais un modèle de
∀x∃yQ(x, y) «donne » un modèle de
∀xQ(x, f (x)). En effet soient I un modèle de
∀x∃yQ(x, y) et D le domaine de I. Pour
tout d∈D, l'ensemble
{e∈D | (d, e)∈QI} n'est
pas vide, donc il existe
g : D→D une fonction 5.1 telle que pour tout d∈D,
g(d )∈{e∈D | (d, e)∈QI}. Soit J l'interprétation J telle
que QJ = QI et fJ = g : J est modèle de
∀xQ(x, f (x)).
5.2.1 Algorithme de skolémisation d'une formule
Nous définissons d'abord les éléments nécessaires pour présenter la
forme de Skolem, ensuite nous donnons un algorithme de skolémisation.
Définition 5.2.3 (Formule propre)
Une formule fermée est dite propre,
s'il elle ne comporte pas de variable liée par deux quantificateurs
distincts.
Exemple 5.2.4
Les formules
∀xP(x)∨∀xQ(x) et
∀x(P(x)⇒∃xQ(x)∧∃yR(x, y))
Les formules
∀xP(x)∨∀yQ(y) et
∀x(P(x)⇒∃yR(x, y))
Nous étendons la notion de forme normale de la logique des
propositions à la logique du premier ordre en disant qu'une formule
est en forme normale si elle est sans équivalence, ni implication, et
dont les négations portent uniquement sur les formules atomiques.
Définition 5.2.5 (Forme de Skolem)
Soient A une formule fermée et B la formule en forme normale sans
quantificateur obtenue par la transformation ci-après : B est la
forme de Skolem de A.
Il y a plusieurs façons de skolémiser une formule fermée. Nous
proposons un compromis entre l'efficacité et la simplicité de la
transformation. Notre algorithme est consistué de la succession des
quatre étapes suivantes :
- Transformation en formule normale : Transformation de la
formule fermée en une autre formule fermée en forme normale
équivalente.
- Transformation en formule propre : Transformation de la
formule fermée en forme normale en une formule fermée, en forme
normale, propre et équivalente.
- Élimination des quantificateurs existentiels : Cette
transformation préserve seulement l'existence de modèle,
comme nous l'avons vu sur les exemples.
- Transformation en forme de Skolem : Transformation de la formule fermée, en forme normale,
propre et sans quantificateur existentiel en une formule en forme
normale sans quantificateur.
Nous détaillons chacune de ces quatre étapes.
Comme dans le cas propositionnel, nous enlevons les équivalences et
les implications et déplaçons les négations vers les formules
atomiques au moyen des équivalences suivantes utilisées de gauche à
droite :
-
A⇔B≡(A⇒B)∧(B⇒A).
-
A⇒B≡¬A∨B.
-
¬¬A≡A.
-
¬(A∧B)≡¬A∨¬B.
-
¬(A∨B)≡¬A∧¬B.
-
¬∀xA≡∃x¬A.
-
¬∃xA≡∀x¬A.
Remarque 5.2.6
En combinant déplacement de la négation et élimination de
l'implication, c'est-à-dire en remplaçant
¬(A⇒B) par
A∧¬B, nous pouvons effectuer plus rapidement la
transformation en formule normale équivalente, qu'en se limitant aux
équivalences ci-dessus.
Exemple 5.2.7
La formule
∀y(∀xP(x, y)⇔Q(y)) est
transformée par élimination de l'équivalence et de l'implication
en :
En utilisant les résultats sur les changements de variables présentés
dans la section 4.4.3, nous changeons le nom des
variables liées à deux quantificateurs, en choisissant par exemple de
nouvelles variables à chaque changement de nom.
Exemple 5.2.8
La formule
∀xP(x)∨∀xQ(x) est changée en
La formule
∀x(P(x)⇒∃xQ(x)∧∃yR(x, y)) est changée
en
Soit A une formule fermée normale et propre ayant une occurrence de
la sous-formule
∃yB. Soient
x1,…, xn l'ensemble des
variables libres de
∃yB, où n≥ 0. Soit f un symbole
ne figurant pas dans A. Nous remplaçons cette occurrence de
∃yB par
B < y : = f (x1,…, xn) >5.2.
Théorème 5.2.9
Soit A' la formule obtenue en appliquant l'élimination d'un
quantificateur existentiel sur la formule A. La formule A' est
une formule fermée en forme normale et propre vérifiant :
- A' a pour conséquence A (
A'
 A).
A).
- Si A a un modèle alors A' a un modèle identique à celui de
A sauf pour le sens de f.
Preuve :
- Montrons que A' a pour conséquence A. Puisque la formule
A est fermée et propre, les variables libres de
∃yB, qui
sont liées à l'extérieur de
∃yB, ne sont pas liées par des
quantificateurs dans B (sinon la propriété propre ne serait pas
respectée), donc le terme
f (x1,…, xn) est libre pour y
dans B et donc d'après le corollaire 4.3.38 :
B < y : = f (x1,…, xn) > a pour conséquence
∃yB. Nous en
déduisons donc que A' a pour conséquence A.
- Montrons que tout modèle de A donne un modèle de A'.
Supposons que A a un modèle I où I est une interprétation de
domaine D. Soit c∈D et pour tous
d1,…, dn∈D,
soit
Ed1,…, dn l'ensemble des éléments d∈D tels
que la formule B vaut 1 dans l'interprétation I et l'état
x1 = d1,…, xn = dn, y = d de ses variables libres. Soit
g : Dn→D une fonction telle que si
Ed1,…, dn
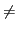 ∅ alors
g(d1,…, dn)∈Ed1,…, dn sinon
g(d1,…, dn) = c5.3. Soit J
l'interprétation identique à I sauf que fJ = g. Nous avons :
∅ alors
g(d1,…, dn)∈Ed1,…, dn sinon
g(d1,…, dn) = c5.3. Soit J
l'interprétation identique à I sauf que fJ = g. Nous avons :
-
[∃yB](I, e) = [B < y : = f (x1,…, xn) > ](J, e),
ceci d'après l'interprétation de f et le théorème 4.3.36,
pour tout état e des variables,
-
[∃yB](I, e) = [∃yB](J, e), puisque le symbole
f est nouveau, la valeur de
∃yB ne dépend pas du sens
de f.
-
∃yB⇔B < y : = f (x1,…, xn) >
 A⇔A', d'après la propriété du
remplacement 1.3.10, qui est aussi vraie en logique du
premier ordre.
A⇔A', d'après la propriété du
remplacement 1.3.10, qui est aussi vraie en logique du
premier ordre.
D'après ces trois points, nous obtenons
[A](J, e) = [A'](J, e) et
puisque f n'est pas dans A et que les formules A et A' n'ont
pas de variables libres, nous avons
[A]I = [A']J. Puisque I est
modèle de A, J est modèle de A'.

Remarque 5.2.10
Dans le théorème 5.2.9, il faut constater que la formule
A' obtenue à partir de la formule A par élimination d'un
quantificateur reste fermée, en forme normale et propre. Donc, en
«appliquant» plusieurs fois le théorème, ce qui implique de choisir
un nouveau symbole à chaque quantificateur éliminé, nous
transformons une formule A fermée, en forme normale et propre en une formule
B fermée, en forme normale, propre et sans quantificateur existentiel
telle que :
- la formule A est conséquence de la formule B,
- si A a un modèle, alors B a un modèle identique sauf pour le
sens des nouveaux symboles.
Exemple 5.2.11
En éliminant les quantificateurs existentiels de la formule
∃x∀yP(x, y)∧∃z∀u¬P(z, u) nous
obtenons
Donc, il faut impérativement utiliser un nouveau symbole lors de
chaque élimination d'un quantificateur existentiel.
Exemple 5.2.12
En éliminant les quantificateurs existentiels de la formule
∃x∀y∃zP(x, y, z) nous
obtenons
Nous pouvons enfin enlever les quantificateurs universels afin
d'obtenir une forme de Skolem.
Théorème 5.2.13
Soit A une formule fermée, en forme normale, propre et sans quantificateur
existentiel. Soit B la formule obtenue en enlevant de A tous les
quantificateurs universels. La formule A est équivalente à la
fermeture universelle de B.
Preuve : Avec les conditions posées sur A, la transformation de A en
∀(B) revient à effectuer tous les remplacements possibles des
sous-formules de la forme suivante :
-
(∀xC)∧D par
∀x(C∧D), où x
non libre dans D,
-
(∀xC)∨D par
∀x(C∨D), où x non
libre dans D,
-
D∧(∀xC) par
∀x(D∧C), où x
non libre dans D,
-
D∨(∀xC) par
∀x(D∨C), où x non
libre dans D.
Puisque chacun de ces remplacements change une formule en une autre
équivalente, les formules A et
∀(B) sont équivalentes.
Propriété 5.2.14
Soit A une formule fermée et B la forme de Skolem de A.
- La formule
∀(B) a pour conséquence la formule A,
- si A a un modèle alors
∀(B) a un modèle.
Donc A a un modèle si et seulement si
∀(B) a un modèle.
Preuve : Soit C la formule fermée en forme normale et propre, obtenue au terme
des deux premières étapes de la skolémisation de A. Soit D le
résultat de l'élimination des quantificateurs existentiels appliquée
à C. D'après la remarque 5.2.10 nous avons :
- la formule D a pour conséquence la formule C,
- si C a un modèle alors D a un modèle.
Puisque les deux premières étapes changent des formules en des
formules équivalentes, A et C sont équivalentes. D'après le
théorème 5.2.13, D est équivalent à
∀(B). Donc nous pouvons remplacer ci-dessus D par
∀(B) et C par A, ce qui prouve le théorème. 
Exemple 5.2.15
Soit
A = ∀x(P(x)⇒Q(x))⇒(∀xP(x)⇒∀xQ(x)). Nous skolémisons ¬A.
- ¬A est transformée en la formule en forme normale :
- La formule en forme normale est transformée en la formule
propre :
- Le quantificateur existentiel est «remplacé» par une constante :
- Les quantificateurs universels sont enlevés :
Cette formule est la forme de Skolem de ¬A suivant la
définition 5.2.5.
Pour skolémiser un ensemble de formules, nous skolémisons chaque
formule de l'ensemble comme il a été indiqué ci-dessus en choisissant
impérativement un nouveau symbole pour chaque quantificateur
existentiel éliminé durant la troisième étape de la skolémisation. Les
raisons pour le choix d'un symbole nouveau apparaissent clairement
dans la preuve du théorème 5.2.9 et dans l'exemple
5.2.11.
Corollaire 5.2.16
En skolémisant un ensemble de clauses fermées Γ, nous obtenons
un ensemble Δ de formules sans quantificateurs tel que :
- Tout modèle de
∀(Δ) est modèle de Γ.
- Si Γ a un modèle alors
∀(Δ) en a un modèle
qui ne diffère de celui de Γ que par le sens des nouveaux
symboles.
La skolémisation a des conséquences pratiques : elle facilite la
preuve d'insatisfiabilité d'une formule. Elle a aussi des conséquences
théoriques, que nous examinons.
Théorème 5.2.17
Soit Γ un ensemble dénombrable de formules fermées.
Si Γ a un modèle alors Γ a un modèle dénombrable.
Preuve : Nous skolémisons Γ en un ensemble Δ de formules sans
quantificateurs. Supposons que Γ a un modèle. Alors
∀(Δ) a un modèle d'après le
corollaire 5.2.16. D'après le
théorème 5.1.16,
∀(Δ) a un modèle de
Herbrand sur la signature de Δ. Puisque l'ensemble Γ
est dénombrable, sa signature l'est aussi, donc aussi celle de
Δ et par suite le domaine de ce modèle de Herbrand est
dénombrable.
Remarque 5.2.18
Appelons théorie, un ensemble de
formules. D'après le théorème, toute théorie dénombrable
qui a un modèle, a un modèle dénombrable. Autrement dit avec
une théorie du premier ordre, nous pouvons parler des
propriétés des nombres réels ou des ensembles, mais nous ne
pouvons pas obliger notre théorie à n'avoir que des modèles non
dénombrables, bien que l'ensemble des réels ou la classe de tous
les ensembles ne soient pas dénombrables.
Après la skolémisation des formules et avant de pouvoir appliquer une
généralisation au premier ordre de la méthode de résolution il faut
transformer les formes de Skolem en clauses comme nous l'avons fait en
logique propositionnelle. Nous étendons donc les notions essentielles
à cette transformation avant de donner les règles permettant cette
transformation.
Définition 5.2.19 (Littéral positif, négatif et clause)
Un littéral positif est une formule
atomique. Un littéral négatif est la
négation d'une formule atomique.
Nous remarquons que tout littéral est positif ou négatif, et nous
rappelons qu'une clause est une somme de littéraux.
Définition 5.2.20 (Forme clausale d'une formule)
Soit A une formule fermée, la forme clausale de A est un ensemble de clauses obtenu en deux étapes :
- Skolémisation de A, autrement dire construire B la forme de
Skolem de A.
- Remplacement de B par un ensemble Γ équivalent de
clauses obtenu par distributivité de la somme sur le produit.
Propriété 5.2.21
La fermeture de la forme clausale d'une formule fermée a un modèle si
et seulement la formule a un modèle. Plus précisément :
- la fermeture de la forme clausale d'une formule a pour
conséquence la formule,
- si la formule a un modèle alors la fermeture de sa forme
clausale en a un.
Preuve : Soient A une formule fermée, B sa forme de Skolem et
Γ sa forme clausale. D'après les propriétés de la
skolémisation :
-
∀(B) a pour conséquence A.
- Si A a un modèle alors
∀(B) a un modèle.
Puisque Γ est obtenu par distributivité, B et Γ sont
équivalents donc
∀(B) et
∀(Γ) sont aussi
équivalents. Par suite dans les deux propriétés ci-dessus, nous
pouvons remplacer
∀(B) par
∀(Γ).
Définition 5.2.22 (Forme clausale d'un ensemble de
formules
)
Soit Γ un ensemble de
formules fermées. Nous définissons la forme clausale de
Γ comme l'union des formes clausales de chacune des formules
de Γ, en prenant soin au cours de la skolémisation
d'éliminer chaque occurrence d'un quantificateur existentiel à
l'aide d'un nouveau symbole.
Corollaire 5.2.23
Soient Γ un ensemble de formules fermées et Δ la forme
clausale de Γ. Nous avons :
-
∀(Δ) a pour conséquence Γ, et
- si Γ a un modèle alors
∀(Δ) a un modèle.
Théorème 5.2.24 (Adaptation du théorème de Herbrand aux formes clausales)
Soient Γ un ensemble de formules fermées et Δ la forme
clausale de Γ. L'ensemble Γ est insatisfaisable si et
seulement s'il existe un sous-ensemble fini insatisfaisable
d'instances des clauses de Δ sur la signature de Δ.
Preuve : D'après l5.2.23, la skolémisation
préserve la satisfaisablité, donc : Γ est insatisfaisable si
et seulement si
∀(Δ) est insatisfaisable. D'après le
corollaire du théorème de Herbrand 5.1.18,
∀(Δ) est insatisfaisable si et seulement s'il existe un
sous-ensemble fini insatisfaisable d'instances des clauses de
Δ sur la signature de Δ.
Exemple 5.2.25
Soit
A = ∃y∀z(P(z, y)⇔¬∃x(P(z, x)∧P(x, z))). Calculons la forme clausale de A.
- Mettre A sous forme en forme normale :
- Rendre propre le résultat :
- Éliminer les quantificateurs existentiels :
- Supprimer les quantificateurs universels, nous obtenons la
forme de Skolem de A :
- Transformer en produit de sommes de littéraux, nous obtenons la
forme clausale de A, qui est l'ensemble suivant de clauses :
D'après la propriété ci-dessus, A n'a pas de modèle si et seulement
s'il y a un ensemble fini insatisfaisable d'instances de
C1, C2, C3
sur la signature de ces clauses. Nous recherchons ces instances :
5.3 Unification
Après la mise en forme clausale d'un ensemble de formules en logique
du premier ordre et avant de généraliser la résolution pour ces
clauses, nous avons besoin d'un algorithme résolvant l'égalité
entre deux termes. Étant donné deux termes, trouver une
substitution qui appliquée à ces deux termes les rendent égaux
est appelé problème d'unification de ces deux termes. Ce
problème a intéressé de grands noms de l'informatique comme Alan
Robinson [23], Gérard
Huet [15,16], Alberto
Martelli et Ugo
Montanari [21],
ou encore plus récemment Franz
Baader et Ayne
Snyder [3].
Définition 5.3.1 (Expression, solution)
Appelons expression, un terme ou un
littéral. Une substitution σ (voir
définition 5.1.3) est solution de
l'équation e1 = e2 entre deux
expressions, si les deux expressions e1σ et e2σ sont
identiques. Une substitution est solution d'un ensemble
d'équations si elle est solution de chaque équation de l'ensemble.
Définition 5.3.2 (Unificateur)
Soient σ une substitution et E un ensemble d'expressions.
Eσ = {tσ | t∈E}. La substitution σ est un
unificateur de E si et seulement si l'ensemble Eσ n'a qu'un
élément. Soit
{ei| 1≤i≤n} un ensemble fini
d'expressions. La substitution σ est un unificateur de cet
ensemble si et seulement si elle est solution du système d'équations
{ei = ei+1| 1≤i < n}.
Définition 5.3.3 (Support d'une substitution)
Le support d'une substitution σ est l'ensemble des
variables x telles que
xσ 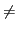 x. Dans la suite, nous nous
intéressons seulement aux substitutions à support fini, c'est à dire
qui ne changent qu'un nombre fini de variables. Une substitution
σ à support fini est notée
< x1 : = t1,…, xn : = tn > ou plus simplement
x1 : = t1,…, xn : = tn quand il n'y a
pas de risque d'ambiguïté. Les variables
x1,…, xn sont
distinctes et la substitution vérifie :
x. Dans la suite, nous nous
intéressons seulement aux substitutions à support fini, c'est à dire
qui ne changent qu'un nombre fini de variables. Une substitution
σ à support fini est notée
< x1 : = t1,…, xn : = tn > ou plus simplement
x1 : = t1,…, xn : = tn quand il n'y a
pas de risque d'ambiguïté. Les variables
x1,…, xn sont
distinctes et la substitution vérifie :
- Pour i de 1 à n,
xiσ = ti.
- Pour toute variable y telle que
y
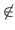 {x1,…, xn}, nous avons :
yσ = y.
{x1,…, xn}, nous avons :
yσ = y.
Exemple 5.3.4
L'équation
P(x, f (y)) = P(g(z), z) a pour solution :
Le système d'équations
x = g(z), f (y) = z a pour solution :
Définition 5.3.5 (Composition de substitutions)
Soient σ et τ deux substitutions, nous notons
στ la
substitution telle que pour toute variable x,
xστ = (xσ)τ. La substitution
στ est une instance de
σ. Deux substitutions sont équivalentes si chacune d'elles est
une instance de l'autre.
Exemple 5.3.6
Considérons les substitutions suivantes :
-
σ1 = < x : = g(z), y : = z >.
-
σ2 = < x : = g(y), z : = y >.
-
σ3 = < x : = g(a), y : = a, z : = a >.
Nous avons les relations suivantes entre ces substitutions :
Définition 5.3.7 (Solution la plus générale)
Une solution d'un système d'équations est appelée la plus
générale (en français nous disons aussi principale) si
toute autre solution en est une instance. Notons que deux solutions
«les plus générales » sont équivalentes.
Exemple 5.3.8
L'équation
f (x, g(z)) = f (g(y), x) a pour solution :
Définition 5.3.9 (Unificateur le plus général)
Soit E un ensemble d'expressions. Nous rappelons qu'une expression
est un terme ou un littéral. Un unificateur de E (voir définition
5.3.2) est appelé le plus
général (ou encore principal), si tout autre unificateur en est
une instance.
Remarque 5.3.10 (Unificateur le plus général et solution la plus générale)
Soit
E = {ei | 1≤i≤n} un ensemble d'expressions. Dans la définition d'un
unificateur, nous avons indiqué que σ est un unificateur de E si et seulement si
σ est solution du système
S = {ei = ei+1 | 1≤i < n}.
Donc l'unificateur le plus général de E est la solution la plus générale de S.
L'algorithme calculant la solution d'un système d'équations est
appelé algorithme d'unification car la recherche d'un unificateur d'un ensemble
d'expression se réduit à la recherche de la solution d'un
système d'équations. L'algorithme sépare les équations en
équations à résoudre, notées par une égalité et
équations résolues, notées par le signe : =. Initialement, il
n'y a pas d'équations résolues. L'algorithme applique les
règles énoncées ci-dessous. Il s'arrête quand il n'y a plus
d'équations à résoudre ou quand il a déclaré que le
système à résoudre n'a pas de solution. Quand il s'arrête
sans avoir déclaré l'absence de solution, la liste des équations
résolues est la solution la plus générale du système initial
d'équations.
Notre algorithme d'unification consiste à appliquer les six règles
suivantes :
- Supprimer. Si les deux membres d'une équation sont
identiques, l'équation est supprimée5.4.
- Décomposer. Si les 2 membres d'une équation sont distincts
et commencent par le même symbole alors :
- Une équation de la forme
¬A = ¬B est remplacée par A = B.
- Une équation de la forme
f (s1,…, sn) = f (t1,…, tn)
est remplacée par les équations
s1 = t1,…, sn = tn. Pour
n = 0, cette décomposition supprime l'équation.
- Échec de la décomposition. Si une équation à résoudre
est de la forme
f (s1,…, sn) = g(t1,…, tp) avec
f
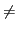 g alors l'algorithme déclare qu'il n'y a pas de solution. En
particulier il y a évidemment un échec si nous cherchons à résoudre
une équation entre un littéral positif et un littéral négatif ou
bien si nous avons une constante et une fonction.
g alors l'algorithme déclare qu'il n'y a pas de solution. En
particulier il y a évidemment un échec si nous cherchons à résoudre
une équation entre un littéral positif et un littéral négatif ou
bien si nous avons une constante et une fonction.
- Orienter. Si une équation est de la forme t = x où t est un
terme qui n'est pas une variable et x une variable, alors nous
remplaçons l'équation par x = t.
- Élimination d'une variable :
Si une équation à résoudre est de la forme x = t où
x est une variable et t un terme ne contenant pas x alors :
- Enlever des équations à résoudre x = t.
- Remplacer x par t dans toutes les équations (non résolues
et résolues) 5.5.
- Ajouter x : = t à la partie résolue.
- Échec de l'élimination : Si une équation à résoudre est
de la forme x = t où x est une variable et t un terme distinct
de x et contenant x alors l'algorithme déclare qu'il n'y
a pas de solution.
Exemple 5.3.11
Nous appliquons cet algorithme afin de résoudre les équations
suivantes :
-
f (x, g(z)) = f (g(y), x).
-
f (x, x, a) = f (g(y), g(a), y).
-
f (x, x, x) = f (g(y), g(a), y).
Nous montrons d'abord que notre algorithme est correct, c'est-à-dire
qu'il calcule bien un unificateur. Ensuite nous démontrons qu'il
termine toujours.
Nous observons facilement les trois faits suivants :
- (1) : les règles de suppression, de décomposition,
d'orientation et d'élimination des variables préservent l'ensemble
des solutions.
- (2) : initialement et après toute application de règle,
l'ensemble des équations résolues forme une substitution
x1 : = t1,…, xn : = tn où
x1,…, xn sont des variables
distinctes ne figurant pas dans les termes
t1,…, tn. Soit
σ cette substitution. Il est clair que
tiσ = ti
ainsi σ est solution des équations résolues.
- (3) : Les règles d'échec déclarent correctement l'absence de solution.
De (1) et (2), il résulte que si l'algorithme termine sans échec, la
substitution σ trouvée est la solution la plus générale du
système initial. En effet :
- σ est une solution, puisque, d'après (2), elle est
solution du système terminal et que, d'après (1), l'ensemble
des solutions est préservé par les règles.
- σ est une solution la plus générale, puisque, d'après
(1), toute autre solution est une solution du système terminal, donc
une instance de la substitution définie par ce système.
De (1) et de (3), il résulte que si l'algorithme déclare un échec,
alors le système initial n'a pas de solution. En effet, dans ce cas :
- si le système initial avait une solution, d'après (1), elle
serait solution du système terminal,
- d'après (3), le système terminal n'a pas de solution.
- Les règles de suppression et de décomposition font décroître
strictement la somme des longueurs des termes qui sont de part et
d'autre des équations.
- La règle d'orientation fait décroître strictement la somme des
longueurs des termes qui sont à gauche des équations.
- La règle d'élimination fait décroître strictement le nombre de
variables des équations non résolues.
Il résulte que l'algorithme d'unification termine.
Nous avons maintenant tous les ingrédients pour présenter la
résolution au premier ordre. Bien entendu nous transformons un
ensemble de formules en forme clausale. Ensuite nous pouvons appliquer
trois règles permettant de «factoriser » des termes, de «
copier » une clause et enfin de faire une «résolution binaire
». Ces différentes règles utilisent l'algorithme d'unification
précédemment. Par la suite, nous montrons la cohérence et la
complétude de ce système formel. La complétude est basée sur
le théorème de Herbrand dans la version donnée dans le
corollaire 5.2.24.
Soit Γ un ensemble de clauses, nous supposons que
∀(Γ) n'a pas de modèle, nous proposons alors un système
formel permettant de déduire  de Γ avec les trois règles
suivantes :
de Γ avec les trois règles
suivantes :
- La factorisation qui de la prémisse
P(x, f (y))∨P(g(z), z)∨Q(z, x) déduit
P(g(f (y)), f (y))∨Q(f (y), g(f (y))). La clause déduite est obtenue en calculant la
solution la plus générale
x : = g(f (y)), z : = f (y) de
P(x, f (y)) = P(g(z), z).
- La règle de copie qui permet de renommer les variables d'une
clause.
- La résolution binaire (RB) qui des deux prémisses sans variable
commune
P(x, a)∨Q(x) et
¬P(b, y)∨R(f (y)) déduit le
résolvant
Q(b)∨R(f (a)), en calculant la solution plus
générale
x : = b, y : = a de
P(x, a) = P(b, y).
Pour simplifier la présentation des règles, nous identifierons une
clause, qui est une somme de littéraux, avec l'ensemble de ses
littéraux. Nous formalisons ces trois règles.
Propriété 5.4.1
Soient A une formule sans quantificateur et B une instance de A.
Nous avons :
∀(A)  ∀(B).
∀(B).
Preuve : Soit I une interprétation quelconque. Puisque
∀(A) et
∀(B) n'ont pas de variables libres, il suffit de montrer que
si I est modèle de
∀(A) alors I est modèle de
∀(B). Supposons I modèle de
∀(A). D'après le lemme
5.1.11, pour tout état e, (I, e) est modèle de
B. D'après le lemme 5.1.9, I est
modèle de
∀(B).
Définition 5.4.2
La clause C' est un facteur de la clause C
si C' = C ou s'il existe un sous-ensemble E de C tel que E a
au moins deux éléments, E est unifiable et
C' = Cσ où
σ est l'unificateur le plus général de E.
Nous obtenons immédiatement la propriété suivante.
Propriété 5.4.4 (Cohérence de la règle de factorisation)
Soit C' un facteur de la clause C. Nous avons :
∀(C)  ∀(C').
∀(C').
Preuve : Puisque C' est une instance de C, la propriété est une conséquence
immédiate de la propriété 5.4.1.
5.4.1.2 Copie d'une clause
Définition 5.4.5
Soient C une clause et σ une substitution, qui ne change que
les variables de C et dont la restriction aux variables de
C est une bijection entre ces variables et celles de la
clause Cσ.
La clause Cσ est une copie de la clause C.
La substitution
σ est aussi appelée un renommage de
C.
Définition 5.4.6
Soient C une clause et σ un renommage de C. Soit f la
restriction de σ aux variables de C et f-1
l'application réciproque de f. Soit
σ-1C la
substitution ainsi définie pour toute variable x :
- Si x est une variable de Cσ alors
xσ-1C = xf-1 (par soucis de clarté, nous avons préféré utiliser la
notation postfixée xf-1 plutôt que la notation préfixée
f-1(x), plus usuelle).
- Sinon
xσ-1C = x.
Cette substitution est appelée l'inverse du
renommage σ de C.
Exemple 5.4.7
Soit
σ = < x : = u, y : = v >. σ est un renommage du littéral
P(x, y). Le littéral P(u, v), où
P(u, v) = P(x, y)σ, est une copie de P(x, y).
Soit
τ = < u : = x, v : = y >. τ est l'inverse du renommage σ de P(x, y).
Notons que
P(u, v)τ = P(x, y) : le littéral P(x, y) est une copie de P(u, v) par le
renommage τ.
Propriété 5.4.8
Soient C une clause et σ un renommage de C.
-
σ-1C est un renommage de Cσ.
- Pour toute expression ou clause E, dont les variables sont celles de C,
Eσσ-1C = E.
Donc
Cσσ-1C = C et par suite C est une copie de Cσ.
Preuve : Soit f la restriction de σ aux variables de C. Par définition du renommage, f
est une bijection entre les variables de C et celles de Cσ.
- Par définition de
σ-1C, cette substitution ne change que les variables
de Cσ et sa restriction aux variables de Cσ est la bijection f-1.
Donc,
σ-1C est un renommage de Cσ.
- Soit x une variable de C. Par définition de f,
xσσ-1C = xff-1 = x. Donc, par une récurrence omise
et sans intérêt sur les termes, littéraux et clauses, pour toute
expression ou clause E, dont les variables sont celles de C,
nous avons
Eσσ-1C = E.

Propriété 5.4.9
Soient deux clauses copies l'une de l'autre, leurs fermetures
universelles sont équivalentes.
Preuve : Soit C' une copie de C. Par définition, C' est une instance de
C et par la propriété précédente, C est une copie de C', donc
une instance de C. Donc par la propriété 5.4.1, la
fermeture universelle de C est conséquence de celle de C' et
inversement. Par suite, ces deux fermetures sont équivalentes.
Définition 5.4.10
Soient C et D deux clauses n'ayant pas de
variable commune. La clause E est un résolvant
binaire de C et
D s'il y a un littéral L∈C et un littéral M∈D tels
que L et Mc (le littéral opposé à M) sont unifiables et
si
E = ((C - {L})∪(D - {M}))σ où σ est la
solution la plus générale de l'équation L = Mc.
Propriété 5.4.12 (Cohérence de la règle de résolution
binaire)
Soit E un résolvant binaire des
clauses C et D, nous avons :
∀(C),∀(D)  ∀(E).
∀(E).
Preuve : Soit I une interprétation. Puisque les trois formules
∀(C),∀(D),∀(E) sont sans variable libre, il suffit de
montrer que si I est modèle de
∀(C) et de
∀(D)
alors I est modèle de
∀(E). Supposons que I est modèle
de
∀(C),∀(D) et montrons que c'est un modèle de
∀(E). Soit e un état quelconque de cette
interprétation. D'après le lemme 5.1.11, (I, e)
est modèle de Cσ et Dσ. Par définition du résolvant
binaire, il y a un littéral L∈C et un littéral M∈D
tels que L et Mc (le littéral opposé à M) sont
unifiables. Ainsi, Lσ et Mσ sont deux littéraux
opposés, donc (I, e) est modèle soit de l'un, soit de l'autre de
ces deux littéraux.
- Supposons (I, e) modèle de Lσ. Puisque (I, e) est contre-modèle de Mσ
et modèle de Dσ, c'est un modèle de
(D - {M})σ donc de E
car
(D - {M})σ⊂E.
- Supposons (I, e) contre-modèle de Lσ. Puisque c'est un modèle de Cσ,
c'est un modèle de
(C - {L})σ donc de E
car
(C - {L})σ⊂E.
Donc (I, e) est modèle de E. Puisque l'état e est quelconque, d'après
le lemme 5.1.9, I est modèle de
∀(E).
Définition 5.4.13
Soient Γ un ensemble de clauses et C une clause. Une
preuve de C à partir de Γ est une suite de clauses
se terminant par C, toute clause de la preuve étant un
élément de Γ, un facteur d'une clause la précédant
dans la preuve, une copie d'une clause la précédant dans la
preuve ou un résolvant binaire de deux clauses la précédant
dans la preuve.
C est déduite de Γ au premier ordre par les 3 règles de
factorisation, copie et résolution binaire est dénoté par
Γ 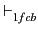 C. Cela signifie qu'il y a une preuve de C
à partir de Γ. Quand il n'y a pas d'ambiguïté sur le
système formel utilisé, nous remplaçons
C. Cela signifie qu'il y a une preuve de C
à partir de Γ. Quand il n'y a pas d'ambiguïté sur le
système formel utilisé, nous remplaçons
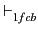 par
par
 .
.
Propriété 5.4.14 (Cohérence)
Soient Γ un ensemble de clauses et C une clause. Si
Γ 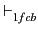 C alors
∀(Γ)
C alors
∀(Γ)  ∀(C).
∀(C).
Preuve : Cette propriété est une conséquence immédiate de la
cohérence de la factorisation, de la copie et de la résolution
binaire. Cette preuve est demandée dans
l'exercice 84.
Exemple 5.4.15
Soient les deux clauses :
-
C1 = P(x, y)∨P(y, x).
-
C2 = ¬P(u, z)∨¬P(z, u).
Montrons par résolution que
∀(C1, C2) n'a pas de modèle.
Cet exemple montre, a contrario, que la résolution binaire seule est
incomplète, sans la factorisation, nous ne pouvons pas déduire la
clause vide.
Exemple 5.4.16
Soient les trois clauses :
-
C1 = ¬P(z, a)∨¬P(z, x)∨¬P(x, z).
-
C2 = P(z, f (z))∨P(z, a).
-
C3 = P(f (z), z)∨P(z, a).
Nous donnons une preuve par résolution que
∀(C1, C2, C3)
n'a pas de modèle. Dans cette preuve RB 1(3), 3(1) signifie par
résolution binaire sur le 3olittéral de la clause 1 et le 1o
littéral de la clause 3.
Nous définissons une nouvelle règle, la résolution au 1o
ordre, qui est une combinaison des trois règles de factorisation,
copie et résolution binaire. Ceci nous permettra de prouver la
complétude de la résolution.
Définition 5.4.17
La clause E est un résolvant au 1oordre des
clauses C et D si E est un résolvant binaire de C' et D'
où C' est un facteur de C et D' est une copie sans variable
commune avec C' d'un facteur de D. La règle qui de C et D
déduit E est appelée la résolution de 1oordre.
Exemple 5.4.18
Soient
C = ¬P(z, a)∨¬P(z, x)∨¬P(x, z) et
D = P(z, f (z))∨P(z, a).
Soient Γ un ensemble de clauses et C une clause, nous avons
défini jusqu'à présent trois notions de preuve par résolution que nous
distinguons en notant par:
-
Γ
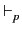 C le fait qu'il y existe une preuve de C à
partir de Γ obtenue par résolution propositionnelle,
autrement dit sans substitution.
C le fait qu'il y existe une preuve de C à
partir de Γ obtenue par résolution propositionnelle,
autrement dit sans substitution.
-
Γ
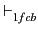 C le fait qu'il y existe une preuve de
C à partir de Γ par factorisation, copie et résolution
binaire.
C le fait qu'il y existe une preuve de
C à partir de Γ par factorisation, copie et résolution
binaire.
-
Γ
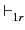 C le fait qu'il y existe une preuve de C
à partir de Γ obtenue par résolution de 1oordre.
C le fait qu'il y existe une preuve de C
à partir de Γ obtenue par résolution de 1oordre.
Puisque la résolution du premier ordre est une combinaison des règles
factorisation, copie et résolution binaire, nous avons immédiatement
Γ 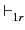 C implique
Γ
C implique
Γ 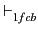 C.
C.
Théorème 5.4.19 (Théorème du relèvement)
Soient C et D deux clauses. Soient C' une instance de C et D'
une instance de D. Soit E' un résolvant propositionnel de
C' et D', il existe E un résolvant au premier ordre de C
et D qui a pour instance E'.
Preuve : La preuve consiste essentiellement à construire E.
Puisque C' est une instance de C, il existe une substitution
σ telle que
C' = Cσ.
Puisque D' est une instance de D, il existe une substitution
τ telle que
D' = Dτ.
Puisque E' est un résolvant propositionnel de C' et D', il y a
deux littéraux l'∈C' et m'∈D' tels que :
- l' et m' sont des littéraux opposés, autrement dit
l' = m'c.
-
E' = (C' - {l'})∪(D' - {m'}).
Soit L l'ensemble de tous les littéraux de C tels que
Lσ = {l'}.
Soit M l'ensemble de tous les littéraux de D tels que
Mτ = {m'}.
Puisque L est unifiable, il existe σ' un
unificateur le plus général de L. Puisque σ' unifie L, il
existe un littéral l tel que
Lσ' = {l}. Puisque σ'
est l'unificateur le plus général de L, il existe σ" tel que
σ = σ'σ", d'après la définition
5.3.9.
Puisque M est unifiable, il
existe τ' un unificateur le plus général de M. Puisque τ'
unifie M, il existe un littéral m tel que
Mτ' = {m}.
Puisque τ' est l'unificateur le plus général de M, il existe
τ" tel que
τ = τ'τ", d'après la définition
5.3.9.
Soit ρ un renommage de
Dτ' tel que
Dτ'ρ est une copie de Dτ' sans variable
commune avec Cσ'. Nous montrons qu'il y a un résolvant binaire
E de Cσ' et
Dτ'ρ dont E' est une
instance.
Montrons que l et mcρ sont unifiables. Nous
définissons de la façon suivante un unificateur π de ces deux
littéraux. Soit x une variable quelconque :
- si x est une variable de Cσ' alors
xπ = xσ",
- si x est une variable de
Dτ'ρ alors
xπ = xρ-1Dτ'τ",
- sinon xπ = x.
Notons tout d'abord que π est bien défini, car Cσ' et
Dτ'ρ n'ont pas de variable commune.
- Puisque les variables de Lσ' sont des variables de
Cσ', nous avons
Lσ'π = Lσ'σ" = Lσ = {l'}. Puisque
Lσ' = {l}, nous avons
{l}π = {l'}.
- Puisque les variables de
Mτ'ρ sont des variables de
Dτ'ρ, nous avons
Mτ'ρπ = Mτ'ρρ-1Dτ'τ". Puisque les variables de
Mτ' sont des variables de Dτ', alors d'après la propriété
du renommage inverse 5.4.8, nous avons
Mτ'ρρ-1Dτ' = Mτ'. Par suite
Mτ'ρπ = Mτ'τ" = Mτ = {m'}. Puisque
Mτ' = {m}, nous avons
{m}ρπ = {mρ}π = {m'}.
Puisque l' = m'c, la substitution π est bien, comme il a été
annoncé ci-dessus, un unificateur de l et de mcρ. Par suite,
il exite π' un unificateur le plus général de ces deux littéraux
et il existe π" tel que
π = π'π". Soit
E = ((Cσ' - {l})∪(Dτ'ρ - {mρ}))π'.
- E est un résolvant binaire de Cσ' et de
Dτ'ρ
sans variable commune avec Cσ'. En effet
l∈Cσ',
mρ∈Dτ'ρ et
lπ' = mcρπ'. Puisque Cσ'
est un facteur de C, que Dτ' est un facteur de D et que
Dτ'ρ est une copie de Dτ' sans variable commune avec
Cσ', alors, d'après la définition 5.4.17, E est
un résolvant du premier ordre de C et D.
- Montrons que
Eπ" = E'. donc que E' est une instance de
E. En effet par définition de E et le fait que
π = π'π", nous avons :
Eπ" = ((Cσ' - {l})∪(Dτ'ρ - {mρ}))π = ((Cσ'π - {l}π)∪(Dτ'ρπ - {mρ}π). Comme nous l'avons vu ci dessus :
{l}π = {l'} et
{mρ}π = {m'}. Puisque π est
identique à σ" sur les variable de Cσ', nous avons
Cσ'π = Cσ'σ" = Cσ = C'. Puisque π est
identique à
ρ-1Dτ'τ" sur les variable de
Dτ'ρ, nous avons
Dτ'ρπ = Dτ'ρρ-1Dτ'τ". D'après les propriétés du
renommage inverse 5.4.8, nous avons :
Dτ'ρρ-1Dτ'τ" = Dτ'τ" = Dτ = D'. Donc
Eπ" = (C' - {l'})∪(D' - {m'}) = E'.

Exemple 5.4.20
Soient
C = P(x)∨P(y)∨R(y) et
D = ¬Q(x)∨P(x)∨¬R(x)∨P(y).
- Les clauses
C' = P(a)∨R(a) et
D' = ¬Q(a)∨P(a)∨¬R(a) sont des instances respectivement de C et
D.
- La clause
E' = P(a)∨¬Q(a) est un résolvant
propositionnel de C' et D'.
- La clause
E = P(x)∨¬Q(x) est un résolvant au 1o
ordre de C et D qui a pour instance E'.
Théorème 5.4.21
Soient Γ un ensemble de clauses et Δ un ensemble
d'instances des clauses de Γ, et
C1,…, Cn une preuve
par résolution propositionnelle à partir de Δ, il existe une
preuve
D1,…, Dn par résolution 1oordre à partir
Γ telle que pour i de 1 à n, la clause Ci est une
instance de Di.
Preuve : Nous effectuons une récurrence sur n. Soit
C1,…, Cn, Cn+1 une preuve par résolution propositionnelle à partir de
Δ. Par récurrence, il existe une preuve
D1,…, Dn par
résolution 1oordre à partir Γ telle que pour i de 1 à
n, la clause Ci est une instance de Di. Nous distinguons deux
cas :
- Supposons
Cn+1∈Δ. Il existe
E∈Γ dont
Cn+1 est une instance donc nous prenons Dn+1 = E.
- Supposons que Cn+1 soit un résolvant propositionnel de Cj
et Ck où
j, k≤n. D'après le résultat précédent, il existe
E résolvant au 1oordre de Dj et Dk : nous prenons
Dn+1 = E.

Nous en déduisons immédiatement le corollaire suivant.
Corollaire 5.4.22
Soient Γ un ensemble de clauses et Δ un ensemble
d'instances des clauses de Γ. Supposons que
Δ 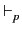 C. Il existe D telle que
Γ
C. Il existe D telle que
Γ 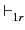 D et C est une
instance de D.
D et C est une
instance de D.
Exemple 5.4.23
Soit l'ensemble de clauses
P(f (x))∨P(u),¬P(x)∨Q(z),¬Q(x)∨¬Q(y). La fermeture universelle de cet ensemble
de clauses est insatisfaisable et nous le montrons de trois manières.
- Par instanciation sur le domaine de Herbrand
{fn(a), n∈
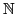 } :
} :
L'ensemble de ces 3 instanciations est insatisfaisable, comme le
montre la preuve par résolution propositionnelle ci-dessous
:
- Cette preuve par résolution propositionnelle est relevée en une
preuve par la règle de résolution au premier ordre :
- Chaque règle de résolution au premier ordre est décomposée en
factorisation, copie et résolution binaire :
Preuve :
- Nous savons que (1) implique (2), car la résolution au 1o
ordre est une combinaison de factorisation, copie et résolution
binaire.
- Nous savons que (2) implique (3), car la factorisation,
la copie et la résolution binaire sont cohérentes.
- Il nous reste à montrer que (3) implique (1). Supposons que
∀(Γ)

 , autrement dit
∀(Γ) est
insatisfaisable. D'après le théorème de Herbrand, il y a Δ un
ensemble fini d'instances sans variable de clauses de Γ qui
n'a pas de modèle propositionnel. Par complétude de la résolution
propositionnelle, nous avons :
Δ
, autrement dit
∀(Γ) est
insatisfaisable. D'après le théorème de Herbrand, il y a Δ un
ensemble fini d'instances sans variable de clauses de Γ qui
n'a pas de modèle propositionnel. Par complétude de la résolution
propositionnelle, nous avons :
Δ 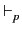
 . D'après le
corollaire au relèvement 5.4.22, il existe D
telle que
Γ
. D'après le
corollaire au relèvement 5.4.22, il existe D
telle que
Γ 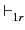 D et
D et  instance de D. Dans ce
cas, nous avons D =
instance de D. Dans ce
cas, nous avons D =  .
.





suivant: 6. Déduction naturelle au
monter: II. Logique du premier
précédent: 4. Logique du premier
Table des matières
Index
Benjamin Wack
2013-01-08
![]() ,
,![]() , car leur sens est fixé dans toute
interprétation :
, car leur sens est fixé dans toute
interprétation : ![]() vaut 1,
vaut 1, ![]() vaut 0, et le symbole = est l'identité sur le
domaine de l'interprétation (voir Remarque 4.3.18).
De plus nous considérons que toute signature comporte
au moins une constante. Ainsi la signature d'un ensemble de formules
ne comportant pas de constante, sera arbitrairement complétée par la
constante a.
vaut 0, et le symbole = est l'identité sur le
domaine de l'interprétation (voir Remarque 4.3.18).
De plus nous considérons que toute signature comporte
au moins une constante. Ainsi la signature d'un ensemble de formules
ne comportant pas de constante, sera arbitrairement complétée par la
constante a.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() de Γ avec les trois règles
suivantes :
de Γ avec les trois règles
suivantes :
![]()
![]()
![]()
![]() C. Cela signifie qu'il y a une preuve de C
à partir de Γ. Quand il n'y a pas d'ambiguïté sur le
système formel utilisé, nous remplaçons
C. Cela signifie qu'il y a une preuve de C
à partir de Γ. Quand il n'y a pas d'ambiguïté sur le
système formel utilisé, nous remplaçons
![]() par
par
![]() .
.
![]() C implique
Γ
C implique
Γ ![]() C.
C.