



suivant: 5. Base de la
monter: II. Logique du premier
précédent: II. Logique du premier
Table des matières
Index
Sous-sections
Ce célèbre syllogisme 4.1 ne peut pas se formaliser en logique
propositionnelle :
Tous les hommes sont mortels;
donc Socrate est mortel.
Pour formaliser un tel raisonnement nous avons besoin d'enrichir la
logique propositionnelle avec de nouveaux connecteurs appelés
quantificateurs, cette logique étendue s'appelle logique du
premier ordre. Elle permet de parler de structures comportant un seul
domaine non vide (contrairement à la logique propositionelle, ce
domaine peut avoir plus de deux valeurs), des fonctions et relations
sur ce domaine. Le langage de cette logique comporte plusieurs
catégories : les termes qui représentent les éléments du domaine ou des
fonctions sur ces éléments, des relations qui relient des termes entre eux
et les formules qui décrivent les interactions entre les
relations grâce aux connecteurs et aux quantificateurs. Par exemple,
la relation mortel (x) désigne x est mortel, la relation homme(x)
signifie que x est un homme. De plus, Socrate est une constante du
domaine (c'est-à-dire, elle a pour valeur un élément du domaine) et
homme(Socrate) signifie que Socrate est un homme. Enfin, la formule
∀x (homme(x)⇒mortel (x)) indique que tous les
hommes sont mortels. À partir de ces deux hypothèses, il est
possible de conclure que Socrate est mortel (
mortel (Socrate)) par
différentes méthodes que nous détaillerons dans cette seconde
partie. Ce même raisonnement s'applique également pour prouver le
syllogisme suivant :
Un cheval bon marché est rare.
Tout ce qui est rare est cher.
Donc un cheval bon marché est cher.
Malgré la conclusion qui semble contradictoire, le raisonnement est
correct. Afin d'obtenir une contradiction il faut ajouter l'hypothèse
suivante :
∀x( bonmarché (x)⇔¬ cher (x)). Ceci traduit la relation communément admise entre
la notion de bon marché et de cher, i.e., tout ce qui est cher
n'est pas bon marché et réciproquement. Avec cette hypothèse
supplémentaire nous pouvons montrer que ce raisonnement est
contradictoire, sans cette hypohèse le raisonnement est correct. Ceci
élucide le paradoxe de ce syllogisme.
Notre objectif dans ce chapitre est d'introduire les concepts et
notions élémentaires de la logique du premier ordre afin de pouvoir
proposer des méthodes de raisonnement dans les chapitres suivants.
Nous commençons par décrire la syntaxe de la
logique du premier ordre. Puis, nous définissons les notions de libre et liée qui sont essentielles pour pouvoir interpréter
le sens des formules. Ensuite nous définissons le sens des formules
que nous pouvons construire à partir de la syntaxe introduite
précédemment. Enfin, nous énonçons des propriétés remarquables de
la logique du premier ordre, qui pourront être utilisées dans les
raisonnements.
Nous ajoutons à la logique propositionnelle deux symboles : le
symbole existentiel (∃) et le symbole universel
(∀). Le symbole existentiel signifie qu'il existe un
élément ayant une certaine propriété alors que le symbole
universel permet de parler de tous les éléments ayant une
propriété. Ces changements impliquent qu'un élément de ce langage
peut désormais dépendre de plusieurs variables. Il faut donc
rajouter dans la syntaxe un délimiteur de variables. Nous avons choisi
classiquement la virgule. Ces changements introduisent de nouveaux
symboles en plus des variables, ces symboles peuvent par exemple
être des nombres sur lesquels nous pouvons créer des fonctions
(comme l'addition) ou encore définir des relations (comme
l'égalité). Toutes ces modifications rendent la présentation de la
syntaxe légèrement plus subtile que celle de la logique
propositionnelle.
Pour écrire les formules de la logique du premier ordre nous étendons
la syntaxe de la logique propositionnelle, ainsi nous disposons du
vocabulaire suivant :
- Deux constantes propositionnelles :
 et
et  représentant
respectivement le faux et le vrai.
représentant
respectivement le faux et le vrai.
- Variables : suite de lettres et de chiffres commençant par une
des minuscules
u, v, w, x, y, z.
- Connecteurs :
¬,∧,∨,⇒,⇔.
- Quantificateurs : ∀ le quantificateur universel et ∃
le quantificateur existentiel.
- Ponctuations : la virgule «, » et les parenthèses ouvrantes
«( » et fermantes «) ».
- Symbole :
- ordinaire : suite de lettres et de chiffres ne commençant pas
par une des minuscules
u, v, w, x, y, z.
- spécial :
+ , - ,*,/, = ,
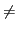 , < ,≤, > ,≥
, < ,≤, > ,≥
L'ensemble des symboles spéciaux peut être augmenté de nouveaux
éléments, suivant les domaines mathématiques étudiés, à condition de
respecter la contrainte que ces nouveaux éléments ne soient pas dans
les ensembles des constantes propositionnelles, des variables, des
connecteurs, des quantificateurs, des ponctuations ou des symboles
ordinaires.
Exemple 4.1.1
Ci-dessous, nous illustrons ces notions :
-
x, x1, x2, y sont des variables,
- homme, parent, succ, 12, 24, f1 sont des symboles
ordinaires, les symboles ordinaires représenteront des fonctions
(constantes numériques ou fonctions à plusieurs arguments) ou des
relations (variables propositionelles ou relations à plusieurs
arguments).
- x = y, z > 3 sont des exemples d'application de symboles
spéciaux.
Nous définissons en toute généralité la notion de terme qui est
essentielle en logique du premier ordre. Nous étendrons dans la suite
cette notion en définissant ce qu'est un terme associé à un ensemble
de symboles.
Définition 4.1.2 (
Terme)
Un terme est défini de manière inductive par :
- un symbole ordinaire est un terme,
- une variable est un terme,
- si
t1,…, tn sont des termes et si s est un symbole
(ordinaire ou spécial) alors
s(t1,…, tn) est un terme.
Exemple 4.1.3
sont des termes, par
contre
n'est pas un terme. Notons que 42(1, y, 3) est
aussi un terme, mais l'usage veut que les noms des fonctions et
relations soient des symboles ordinaires commençant par des lettres.
Définition 4.1.4 (
Formule
atomique)
Nous définissons une
formule atomique de manière inductive par :
 et
et  sont des formules atomiques
sont des formules atomiques
- un symbole ordinaire est une formule atomique
- si
t1,…, tn sont des termes et si s est un symbole
(ordinaire ou spécial) alors
s(t1,…, tn) est une formule
atomique.
Exemple 4.1.5
sont des formules
atomiques, notons également que
ne sont pas des formules atomiques.
Notons que l'ensemble des termes et l'ensemble des formules atomiques
ne sont pas disjoints. Par exemple p(x) est un terme et une formule
atomique. Lorsque t est à la fois un terme et une formule atomique,
nous distinguons
[[t]], le sens de t vu comme un terme de [t],
le sens de t vu comme une formule (voir le paragraphe
4.3.4).
Définition 4.1.6 (
Formule)
Nous définissons une formule de manière inductive
par :
- une formule atomique est une formule,
- si A est une formule alors ¬A est une formule,
- si A et B sont des formules et si o est
une des opérations
∨,∧,⇒,⇔
alors
(AoB) est une formule ,
- si A est une formule et si x est une variable
quelconque alors
∀x A et
∃x A sont des
formules 4.2.
Exemple 4.1.7
sont des formules atomiques, donc des
formules. Par contre
est une formule qui n'est pas atomique.
Nous reprenons les priorités de la logique propositionnelle pour les
connecteurs, et nous ajoutons une priorité identique à celle de la
négation pour les quantificateurs. Dans le tableau 4.1 nous
donnons les priorités des symboles et des connecteurs par ordre
décroissant du haut vers le bas. Nous indiquons seulement deux règles
de formation des formules à priorité, qui les distinguent des
formules complètement parenthésées et permettent d'omettre des
parenthèses ou d'ajouter des nouvelles parenthèses.
Pour abréger l'écriture des termes, certains symboles de fonction
+ , - ,*,/ et certains symboles de relations
= , 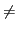 , < ,≤, > ,≥
peuvent être écrits de manière infixe, c'est-à-dire, de façon usuelle.
, < ,≤, > ,≥
peuvent être écrits de manière infixe, c'est-à-dire, de façon usuelle.
Exemple 4.1.8
Nous abrégeons le terme
+ (x,*(y, z)) en x + y*z et
≤(*(3, x), + (y, 5)) en
3*x≤y + 5. La transformation inverse
est définie en donnant aux symboles
= , 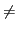 , < ,≤, > ,≥ des
priorités inférieures à celle des symboles + , - ,*,/.
, < ,≤, > ,≥ des
priorités inférieures à celle des symboles + , - ,*,/.
Tableau 4.1:
Priorités des connecteurs et symboles.
| OPéRATIONS |
| - + unaire |
|
| *,/ |
associatif gauche |
| + , - binaire |
associatif gauche |
| RELATIONS |
= , 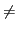 , < ,≤, > ,≥ , < ,≤, > ,≥ |
| NéGATION, QUANTIFICATEURS |
|
¬,∀,∃ |
| CONNECTEURS BINAIRES |
| ∧ |
associatif gauche |
| ∨ |
associatif gauche |
|
⇒ |
associatif droit |
|
⇔ |
associatif gauche |
|
Définition 4.1.9 (
Formule à priorité)
Une formule à priorité est :
- Une formule atomique.
- Si A est une formule à priorité alors ¬A est une formule
à priorité.
- Si A et B sont des formules à priorité alors AoB
est une formule à priorité.
- Si A est une formule à priorité et si x une variable quelconque alors
∀x A et
∃x A sont des formules
à priorité.
- Si A est une formule à priorité alors (A) est une formule à
priorité.
Exemple 4.1.10
La formule (à priorité)
∀xP(x)∧∀xQ(x)⇔∀x(P(x)∧Q(x)) peut être vue comme une
abréviation de la formule
La
formule (à priorité)
∀x∀y∀z(x≤y∧y≤z⇒x≤z) peut être vue comme une abréviation
de la formule
Exemple 4.1.11
La priorité du ∀ est plus forte que celle de
⇒,
dans la formule
∀xP(x)⇒Q(y). Donc, l'opérande
gauche de l'implication est
∀xP(x). La structure de la
formule sera ainsi représentée
par l'arbre suivant :
Le sens de la formule x + 2 = 4 dépend de x : la formule n'est
vraie (en arithmétique) que si x = 2. La variable x est libre dans
cette formule. Par contre, toujours en arithmétique
∀x(x + 2 = 4) est une formule fausse,
∃x(x + 2 = 4) est une formule
vraie car 2 + 2 = 4 et
∀x∀y(x + y = y + x) est une formule
vraie indépendamment des valeurs de x et y. Ces trois formules
n'ont pas de variables libres.
Sur une représentation en arbre, où nous dessinons les structures
des formules en faisant apparaître ∀x et ∃x comme
des sommets de l'arbre, une occurrence liée de la variable x
est une occurrence en dessous d'un sommet ∃x ou ∀x. Une occurrence de x qui n'est pas sous un tel sommet est
libre.
Définition 4.2.1 (
Portée de liaison,
occurrence libre, liée
)
Soient x une variable et A une formule. Dans une formule
∀x A ou
∃x A, la portée de la liaison
pour x est A. Une occurrence de x dans une formule est libre si elle n'est pas dans la portée d'une liaison pour x,
sinon elle est dite liée.
Exemple 4.2.2
Pour voir les occurrences des variables, nous dessinons la structure
de la formule
∀xP(x, y)∧∃zR(x, z), puisque la priorité de ∀ est supérieure
à celle du ∧, nous obtenons :
L'occurrence de x présente
dans P(x, y) est liée, l'occurrence de x présente dans R(x, z) est
libre. L'occurrence de z est liée.
Définition 4.2.3 (Variable libre, liée, formule
fermée)
La variable
x est une variable libre d'une
formule si et seulement s'il y a une occurrence libre de x dans la
formule. Une variable x est une variable
liée d'une formule si et seulement s'il y a
une occurrence liée de x dans la formule. Une formule sans
variable libre est aussi appelée une formule
fermée.
Remarque 4.2.4
Une variable peut-être à la fois libre et liée. Par exemple, dans la
formule
∀xP(x)∨Q(x), x est à la fois libre et liée.
Remarque 4.2.5
Par définition, une variable qui n'apparaît pas dans une formule (0
occurrence) est par définition une variable NON libre de la formule.
Dans la suite, nous définissons en logique du premier ordre, le sens
des connecteurs, des quantificateurs ainsi que de l'égalité.
Aussi, pour définir le sens d'une formule, il suffit d'indiquer la
valeur des variables libres et le sens de ses symboles utilisés. Dans
un premier temps nous expliquons comment nous déclarons un
symbole. Ensuite nous introduisons la notion de signature qui permet
de définir les termes et formules associés. Une fois toutes ces
notions établies nous définissons les interprétations afin de
donner du sens aux formules de la logique du premier ordre.
Afin de donner un sens aux formules de la logique du premier ordre il
nous faut déclarer les symboles utilisés. Nous distinguons en plus des
variables, les symboles de fonctions, par exemple g(x, y), et les
symboles de relation comme
parent(x, y).
Définition 4.3.1 (Déclaration de symbole)
Une déclaration de symbole est
un triplet noté sgn où s est un symbole, g est soit f
(pour fonction) ou r (pour relation), et n est un entier naturel
dénotant le nombre d'arguments de ce symbole, n est aussi appelé
l'arité de s.
Exemple 4.3.2
Les fonctions d'arité 0 constituent les constantes, par exemple
1 et 2 sont des constantes d'arité nulle, mais
parentr2 est
une notation signifiant que parent est employé comme relation
d'arité 2.
De même *f2 est une déclaration annonçant que * est une
fonction 2-aire. Le symbole Ar0 est d'arité 0 et signifie
que A est une variable propositionnelle. Le symbole
hommer1
est d'arité 1 ou unaire et le symbole
gf2 est d'arité 2 ou 2-aire.
Remarque 4.3.3
Lorsque le contexte ou les conventions usuelles comportent une
déclaration implicite d'un symbole, nous omettons l'exposant. Par
exemple, le symbole égal étant toujours employé comme relation à
deux arguments, nous abrégeons la déclaration de symbole = r2 en
=.
En logique du premier ordre nous pouvons choisir le nom des variables
utilisées mais nous avons aussi la possibilité de construire nos
propres constantes (fonctions sans arguments), fonctions, variables
propositionnelles (relations d'arité nulle) et relations. Une signature
est donc l'ensemble des déclarations de symboles autorisés pour
construire des formules. Elle permet de définir les symboles dont le
sens n'est pas fixé a priori, contrairement par exemple aux
constantes  et
et  dont le sens est toujours fixé
respectivement à 1 et 0.
dont le sens est toujours fixé
respectivement à 1 et 0.
Définition 4.3.4 (Signature, constante, symbole de fonction, variable
propositionnelle, et relation)
Une
signature Σ est un ensemble de
déclarations de symboles de la forme sgn. Soient n un entier
strictement positif et Σ une signature, le symbole s est :
- une constante de la signature si et
seulement si
sf0∈Σ
- un symbole de fonction à n
arguments de la signature, si et seulement si
sfn∈Σ
- une variable
propositionnelle de la signature si et seulement si
sr0∈Σ
- un symbole de relation à n
arguments de la signature, si et seulement si
srn∈Σ
Au lieu de dire
0f0, 1f0, + f2,*f2, = r2 est une signature
pour l'arithmétique, nous disons plus simplement qu'une signature
possible pour l'arithmétique comporte 0, 1, + (à deux
arguments), * et =. Sur cet exemple, nous devons préciser que le
symbole plus est utilisé avec deux arguments (car nous pouvons
aussi rencontrer le symbole plus avec un seul argument).
Exemple 4.3.5
Une signature possible pour la théorie des ensembles est ∈, =. Notons que toutes les autres opérations sur les ensembles peuvent
être définies à partir de ces deux symboles.
Définition 4.3.6 (
Symbole surchargé)
Un symbole est surchargé dans une signature, lorsque cette signature
comporte deux déclarations distinctes du même symbole.
Exemple 4.3.7
Il est fréquent d'utiliser des signatures dans lesquelles le signe
moins est surchargé. Il est utilisé simultanément pour obtenir
l'opposé d'un nombre ou faire la soustraction de deux nombres.
Dans la suite, nous nous interdirons d'utiliser des signatures
comportant des symboles surchargés. Cela permet de simplifier les
notations, car une fois que nous avons précisé la signature utilisée,
nous remplaçons une déclaration de symbole par le symbole
lui-même. Nous définissons maintenant les termes associés à une
signature. Nous considérons un ensemble dénombrable de variables
disjoint de l'ensemble de symboles de la signature.
Définition 4.3.8 (
Terme sur une signature)
Soit Σ une signature, un terme sur
Σ est :
- soit une variable,
- soit une constante s où
sf0∈Σ,
- soit un terme de la forme
s(t1,…, tn), où n≥1,
sfn∈Σ et
t1,…, tn sont des termes sur
Σ.
L'ensemble des termes sur la signature Σ est noté
TΣ.
Définition 4.3.9 (
Formule
atomique sur une signature)
Soit Σ une signature, une formule
atomique sur Σ est :
- soit une des constantes
 ,
, ,
,
- soit une variable propositionnelle s où
sr0∈Σ,
- soit de la forme
s(t1,…, tn) où n≥1,
srn∈Σ et où
t1,…, tn sont des termes sur Σ.
Notons que les variables ne sont pas des formules atomiques.
Définition 4.3.10 (
Formule sur une
signature)
Une formule sur une signature Σ est une
formule, dont les sous-formules atomiques sont des formules
atomiques sur Σ (au sens de la
définition 4.3.9).
Nous dénotons l'ensemble des formules sur la signature Σ par
FΣ .
Exemple 4.3.11
∀x (p(x)⇒∃y q(x, y)) est une formule sur
la signature
Σ = {pr1, qr2, hf1, cf0}. Mais c'est
aussi une formule sur la signature
Σ' = {pr1, qr2},
puisque les symboles h et c ne figurent pas dans la formule.
Définition 4.3.12 (
Signature associée à une formule)
La signature associée à une formule est la plus petite
signature Σ telle que la formule est élément de FΣ,
c'est la plus petite signature permettant d'écrire la formule.
Exemple 4.3.13
La signature Σ associée à la formule
∀x (p(x)⇒∃y q(x, y)) est
Définition 4.3.14 (
Signature
associée à un ensemble de formules)
La signature associée à un ensemble de formules est l'union
des signatures associées à chaque formule de l'ensemble.
Exemple 4.3.15
La signature Σ associée à l'ensemble constitué des deux formules
∀x(p(x)⇒∃y q(x, y)),∀u ∀v (u + s(v) = s(u) + v) est
En logique propositionnelle, le sens des formules est uniquement
fixé par les valeurs des variables, en logique du premier ordre le
sens des formules dépend aussi du sens des fonctions et des
relations. Le sens des fonctions et des relations est fixé par une
interprétation.
Définition 4.3.16 (Interprétation
)
Une interprétation I sur une signature Σ est définie
par un domaine D non vide et une application qui à chaque
déclaration de symbole
sgn∈Σ associe sa valeur sgnI
comme suit :
- sf0I est un élément de D.
- sfnI où n≥1 est une fonction de Dn dans D,
autrement dit une fonction à n arguments.
- sr0I vaut 0 ou 1.
- srnI où n≥1 est un sous-ensemble de Dn, autrement
dit une relation à n arguments.
Exemple 4.3.17
Soit l'interprétation I de domaine
D = {1, 2, 3} où la relation
binaire ami est vraie pour les couples (1, 2), (1, 3) et
(2, 3), c'est-à-dire,
amir2I = {(1, 2),(1, 3),(2, 3)}. ami(2, 3) est vraie dans l'interprétation
I. En revanche, ami(2, 1) est fausse dans l'interprétation I.
Remarque 4.3.18
Dans toute interprétation I,
la valeur du symbole = est l'ensemble
{(d, d ) | d∈D},
autrement dit dans toute interprétation le sens de l'égalité est
l'identité sur le domaine de l'interprétation.
Exemple 4.3.19
Considérons une signature suivante.
- Annef0,
Bernardf0 et
Claudef0 : les prénoms
Anne, Bernard, et Claude dénotent des constantes,
- ar2 : la lettre a dénote une relation à deux arguments
(nous lisons a(x, y) comme x aime y) et
- cf1 : la lettre c dénote une fonction à un argument
(nous lisons c(x) comme le copain ou la copine de x).
Une interprétation possible sur cette signature est l'interprétation
I de domaine
D = {0, 1, 2} où :
-
Annef0I = 0,
Bernardf0I = 1, et
Claudef0I = 2.
-
ar2I = {(0, 1),(1, 0),(2, 0)}.
-
cf1I(0) = 1, cf1I(1) = 0, cf1I(2) = 2. Notons que
la fonction cf1I a comme domaine D, ce qui oblige à définir
artificiellement
cf1I(2): Claude, dénoté par 2, n'a ni
copain, ni copine.
Définition 4.3.20 (
Interprétation
d'un ensemble de formules)
L'interprétation d'un ensemble de formules est une
interprétation qui définit seulement le sens de la signature
associée à l'ensemble des formules.
Définition 4.3.21 (
État)
Un état e d'une interprétation est une application de
l'ensemble des variables dans le domaine de l'interprétation.
Définition 4.3.22 (Assignation)
Une assignation est un couple (I, e)
composé d'une interprétation I et d'un état
e.
Exemple 4.3.23
Soient le domaine
D = {1, 2, 3} et l'interprétation I où la
relation binaire ami est vraie uniquement pour les couples
(1, 2), (1, 3) et (2, 3), c'est-à-dire,
amir2I = {(1, 2),(1, 3),(2, 3)}. Soit e l'état qui associe 2 à x et 1
à y. L'assignation (I, e) rend la relation ami(x, y) fausse.
4.3.4 Sens des formules
Nous expliquons maintenant comment évaluer une formule à partir d'une
assignation, c'est-à-dire, une interprétation et un état. Il faut
noter que dans certains cas, l'état de l'assignation est inutile pour
fixer le sens d'une formule.
Remarque 4.3.24
La valeur d'une formule ne dépend que de ses
variables libres et de ses symboles, aussi pour évaluer une formule
sans variable libre, l'état des variables est inutile.
Nous avons alors deux possibilités :
- Pour une formule sans variables libres, il suffit de
donner une interprétation I des symboles de la formule. Dans ce
cas, les assignations (I, e) et (I, e') donnerons la même valeur à
la formule pour tous états e et e'. Ainsi pour tout état e,
nous identifierons (I, e) et I. Selon le contexte, I sera
considéré comme soit une interprétation soit une assignation dont
l'état est quelconque.
- Pour une formule avec des variables libres, nous avons
donc besoin d'une assignation.
Soient Σ une signature, I une interprétation sur Σ de
domaine D et e un état de cette interprétation. Nous souhaitons
connaître la valeur (0 ou 1) de toute formule A sur Σ
dans l'assignation (I, e). Cette valeur sera notée
[A](I, e). Pour cela, nous avons tout d'abord besoin de définir le
sens de chaque terme t sur Σ dans l'assignation (I, e), noté
[[t]](I, e). Ensuite nous devons fixer le sens de chaque
formule atomique B sur Σ dans la même assignation, noté
[B](I, e).
Chacun sait intuitivement comment évaluer un terme : nous remplaçons les variables
par leurs valeurs, les symboles de fonctions par les fonctions qui
leur sont associées et nous appliquons les fonctions. Mais pour
raisonner sur le sens des termes ou écrire un programme d'évaluation
des termes, nous devons formaliser cette évaluation.
Définition 4.3.25 (
Évaluation)
Nous donnons la définition inductive de l'évaluation d'un terme t :
- si t est une variable, alors
[[t]](I, e) = e(t),
- si t est une constante alors
[[t]](I, e) = tf0I,
- si
t = s(t1,…, tn) où s est un symbole et
t1,…, tn sont des termes, alors
[[t]](I, e) = sfnI([[t1]](I, e),…,[[tn]](I, e)).
Dans les exemples, nous remplaçons les variables par leurs
valeurs, nous confondons les symboles et leur sens.
Exemple 4.3.26
Soit I l'interprétation de domaine
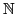 qui
donne aux déclarations de symboles
1f0,*f2, + f2 leur
sens usuel sur les entiers. Soit e l'état tel que
x = 2, y = 3. Calculons
[[x*(y + 1)]](I, e).
qui
donne aux déclarations de symboles
1f0,*f2, + f2 leur
sens usuel sur les entiers. Soit e l'état tel que
x = 2, y = 3. Calculons
[[x*(y + 1)]](I, e).
Définition 4.3.27 (Sens des formules atomiques
)
Le sens des formules atomiques est donné par les règles inductives
suivantes :
-
[
 ](I, e) = 1,[
](I, e) = 1,[ ](I, e) = 0. Dans les exemples, nous
autorisons à remplacer
](I, e) = 0. Dans les exemples, nous
autorisons à remplacer  par sa valeur 1 et
par sa valeur 1 et  par sa valeur 0.
par sa valeur 0.
- Soit s une variable propositionnelle,
[s](I, e) = sr0I.
- Soit
A = s(t1,…, tn) où s est un symbole et
t1,…, tn sont des termes. Si
([[t1]](I, e),…,[[tn]](I, e))∈srnI alors
[A](I, e) = 1 sinon
[A](I, e) = 0.
Remarque 4.3.28
Nous devons distinguer entre évaluer un terme
[[ ]] et évaluer une formule atomique [ ], car dans notre
présentation, ces deux catégories syntaxiques ne sont pas
disjointes, car
s(t1,…, tn) peut être l'application d'une
fonction (
[[]]) ou d'une relation ([ ]). Mais
quand le contexte est sans ambiguïté, nous pouvons omettre cette
distinction.
Exemple 4.3.29
En reprenant l'exemple 4.3.19, nous obtenons :
-
[a(Anne, Bernard )]I =
-
[a(Anne, Claude)]I =
Soit e l'état
x = 0, y = 2. Nous avons :
-
[a(x, c(x))](I, e) =
-
[a(y, c(y))](I, e) =
Attention à distinguer (suivant le contexte), les éléments du domaine
0, 1 et les valeurs de vérité 0, 1. Les exemples suivants mettent
en évidence l'interprétation de l'égalité comme une identité. Dans
l'interprétation I, nous avons :
-
[(Anne = Bernard )]I =
-
[(c(Anne) = Anne)]I =
-
[(c(c(Anne)) = Anne)]I =
Nous pouvons maintenant ajouter le sens des quantificateurs et aussi
celui des opérateurs qui reste identique à celui donné pour la logique
propositionnelle (cf. sous-section 1.2.1).
Définition 4.3.30 (Sens des formules
)
Le sens des formules est donné par :
- Les connecteurs propositionnels ont le même sens qu'en logique
propositionnelle. Soient B et C des formules, rappelons
uniquement le sens de l'implication : si
[B](I, e) = 0 alors
[(B⇒C)](I, e) = 1 sinon
[(B⇒C)](I, e) = [C](I, e).
- Soient x une variable et B une formule.
[∀xB](I, e) = 1 si et seulement si
[B](I, f) = 1 pour tout
état f identique à e, sauf pour x. Soit d∈D. Notons
e[x = d] l'état identique à l'état e, sauf pour la variable x,
auquel l'état e[x = d] associe la valeur d. La définition
ci-dessus peut être mise sous la forme suivante :
[∀
xB]
(I, e) =
mind∈D[
B]
(I, e[x=d]) =
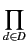
[
B]
(I, e[x=d]),
Cette définition permet de calculer la valeur de
∀xB dans le cas où D est un domaine fini. Mais quand D n'est
pas un domaine fini, c'est seulement une traduction du
quantificateur universel d'un formalisme dans un autre.
-
[∃xB](I, e) = 1 si et seulement s'il y a un
état f identique à e, sauf pour x, tel que
[B](I, f) = 1. La
définition ci-dessus peut être mise sous la forme suivante :
[∃
xB]
(I, e) =
maxd∈D[
B]
(I, e[x=d]) =
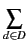
[
B]
(I, e[x=d]),
Exemple 4.3.31
Soit l'interprétation I de domaine
D = {1, 2, 3} où la relation
binaire ami est vraie pour les couples (1, 2), (1, 3) et
(2, 3), c'est-à-dire,
amir2I = {(1, 2),(1, 3),(2, 3)}. La
formule
ami(1, 2)∧ami(2, 3)⇒ami(1, 3) est vraie
dans l'interprétation I, i.e.,
[ami(1, 2)∧ami(2, 3)⇒ami(1, 3)]I = 1.
Exemple 4.3.32
Utilisons l'interprétation I donnée dans
l'exemple 4.3.19. D'après le sens du quantificateur
existentiel, nous devons évaluer a(x, x) pour x = 0,
x = 1, et x = 2. Nous simplifions ce calcul et les calculs suivants en
remplaçant immédiatement les variables par leurs valeurs : cela nous évite
d'utiliser les états.
-
[∃x a(x, x)]I =
-
[∀x∃y a(x, y)]I =
-
[∃y∀x a(x, y)]I =
Remarque 4.3.33
Dans l'interprétation ci-dessus, les formules
∀x∃y a(x, y) et
∃y∀x a(x, y) n'ont pas la même valeur.
Donc en intervertissant un quantificateur existentiel et un
quantificateur universel, nous ne préservons pas le sens des formules.
4.3.5 Modèle, validité, conséquence, équivalence
Ces notions sont définies comme en logique propositionnelle. Mais
alors qu'en logique propositionnelle, une assignation est une
application des variables propositionnelles dans 0, 1, en logique
du premier ordre une assignation est un couple constitué d'une
interprétation des symboles d'une part et de l'état des variables
d'autre part.
Définition 4.3.34 (
Instanciation)
Soit x une variable, t un terme et A une formule.
-
A < x : = t > est la formule obtenue en remplaçant
dans la formule A toute occurrence libre de x par le terme t.
- Le terme t est libre pour x dans A si les variables de t
ne sont pas liées dans les occurrences libres de x dans A.
Exemple 4.3.35
Le terme z est libre pour x dans la formule
∃yp(x, y). Par contre le terme y, comme tout terme comportant la
variable y, n'est pas libre pour x dans cette formule. Soit A
la formule
(∀xP(x)∨Q(x)), la formule
A < x : = b > vaut
Théorème 4.3.36
Soient A une formule et t un terme libre pour la variable x dans
A. Soient I une interprétation et e un état de l'interprétation.
Nous avons
[A < x : = t > ](I, e) = [A](I, e[x=d]), où
d = [[t]](I, e).
Autrement dit, la valeur de
A < x : = t > dans une assignation est la
même que celle de A dans une assignation identique, sauf qu'elle
donne à x la valeur du terme t. Ce théorème, dont le résultat est
évident, peut être prouvé par une récurrence (que nous ne ferons pas)
sur la taille des formules. Nous montrons seulement que la condition
sur t est indispensable en observant un exemple où cette condition
n'est pas respectée.
Exemple 4.3.37
Soient I l'interprétation de domaine {0, 1} avec
pI = {(0, 1)} et e, un état où y = 0. Soient A la formule
∃yp(x, y) et t le terme
y. Ce terme n'est pas libre pour x dans A. Nous avons :
-
A < x : = t > =
et
[A < x : = t > ](I, e) =
- Soit
d = [[t]](I, e) = [[y]](I, e) = 0. Dans l'assignation
(I, e[x = d]), nous avons x = 0. Donc, nous obtenons :
[A](I, e[x=d]) =
Ainsi,
[A < x : = t > ](I, e) 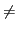 [A](I, e[x=d]), pour
d = [[t]](I, e).
[A](I, e[x=d]), pour
d = [[t]](I, e).
Corollaire 4.3.38
Soient A une formule et t un terme libre pour x dans A. Les
formules
∀xA⇒A < x : = t > et
A < x : = t > ⇒∃xA sont valides.
Ce corollaire est une conséquence immédiate du théorème précédent.
Nous montrons comment rechercher des modèles finis de formules fermées
(c'est-à-dire sans variables libres). Un modèle fini d'une formule
fermée est une interprétation de la formule de domaine fini, qui rend
vraie la formule. Il est clair que le nom des éléments du domaine est
sans importance, aussi quand nous cherchons un modèle avec un domaine
de n éléments, le domaine que nous utiliserons, sera celui des
entiers (sous-entendu naturels) inférieurs à n. Pour savoir si une
formule fermée a un modèle de domaine
{0,…, n - 1}, il suffit
d'énumérer toutes les interprétations possibles de la signature
associée à la formule et d'évaluer la formule pour ces
interprétations. Mais cette méthode est inutilisable en pratique, car
le nombre de ces interprétations est énorme. Soit une signature avec
une constante, un symbole de fonction à un argument et un symbole de
relation à deux arguments (plus éventuellement l'égalité de sens
fixé), sur un domaine à 5 éléments, cette signature à
5×55×225 = 524288000000 interprétations. Aussi nous montrons
d'abord, comment dans le cas où une formule n'a aucun symbole de
fonction et aucune constante, sauf des représentations d'entiers
inférieurs à n, nous pouvons rechercher ses modèles à n
éléments par réduction au cas propositionnel. En présence de symboles
de fonctions et de constantes, nous pouvons en énumérer leurs valeurs,
puis appliquer les méthodes ci-dessous. Pour trouver des énumérations
intelligentes, nous conseillons de lire le manuel de
Prover9 [22].
Nous distinguons dans la suite un entier n et sa représentation
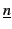 . Par exemple l'entier 3 peut être représenté en base
10 par 3, en base 2 par 11, en chiffres romains par III, en
chiffre grec par γ. Par habitude, nous choisissons la
représentation en base 10. Dans la suite, de façon implicite,
toutes les interprétations considérées donnent à la représentation
d'un entier, la valeur de l'entier représenté.
. Par exemple l'entier 3 peut être représenté en base
10 par 3, en base 2 par 11, en chiffres romains par III, en
chiffre grec par γ. Par habitude, nous choisissons la
représentation en base 10. Dans la suite, de façon implicite,
toutes les interprétations considérées donnent à la représentation
d'un entier, la valeur de l'entier représenté.
Dans certains cas il est suffisant de regarder les expansions de
taille finie afin de trouver un modèle ou un contre-modèle pour une
formule donnée.
Exemple 4.3.40
La 2-expansion de la formule
∃xP(x)⇒∀xP(x) est la formule
Théorème 4.3.41
Soient n un entier et A une formule ne comportant que des
représentations d'entiers de valeur inférieure à n. Soit B la
n-expansion de A. Toute interprétation de domaine
{0,…, n - 1} attribue la même valeur à A et à B.
La condition sur A est nécessaire car si A comporte une
représentation d'un entier au moins égal à n, la valeur de cette
représentation ne sera pas dans le domaine de l'interprétation. La
preuve du théorème est une récurrence sur la taille des formules, que
nous ne ferons pas. Nous nous contentons de montrer que chaque
élimination d'un quantificateur universel conserve la valeur de la
formule fermée
∀xB.
Soient (I, e) une interprétation et un état de domaine
{0,…, n - 1} donnant à la représentation d'un entier, la valeur de l'entier
représenté. Par définition du sens du quantificateur universel :
[∀xB](I, e) = 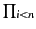 [B](I, e[x=i]). D'après le
théorème 4.3.36 et le fait que la valeur de la représentation
de l'entier i est i, nous avons :
[B](I, e[x=i]) = [B < x : =
[B](I, e[x=i]). D'après le
théorème 4.3.36 et le fait que la valeur de la représentation
de l'entier i est i, nous avons :
[B](I, e[x=i]) = [B < x : = 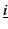 > ](I, e). Par suite :
[∀xB](I, e) =
> ](I, e). Par suite :
[∀xB](I, e) = 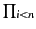 [B < x : =
[B < x : = 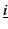 > ](I, e) = [
> ](I, e) = [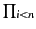 B < x : =
B < x : = 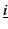 > ](I, e).
> ](I, e).
Soient n un entier et A une formule fermée, sans quantificateur,
sans égalité, sans symbole de fonction, sans constante sauf des
représentations d'entiers inférieurs à n. Soit P l'ensemble des
formules atomiques de A (sauf  et
et  dont le sens est
fixé).
dont le sens est
fixé).
Théorème 4.3.42
Soit v une assignation propositionnelle de P dans {0, 1} alors
il existe une interprétation I de A telle que
[A]I = [A]v.
Preuve : Soit v une assignation propositionnelle de P dans {0, 1}.
Soit I l'interprétation suivante de A :
- Domaine :
{0,…, n - 1}
-
sr0I = v(s) si et seulement si s∈P
- Soit p≥1 et srp un symbole de relation de A . Alors
srpI = {(k1,…, kp)| s(
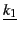 ,…,
,…,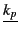 )∈P etv(s(
)∈P etv(s(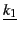 ,…,
,…,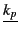 )) = 1}
)) = 1}
Par définition de I, l'assignation v et l'interprétation I
donnent la même valeur aux sous-formules atomiques de A, donc (par récurrence
sur les formules) la
même valeur à la formule A.
Exemple 4.3.43
L'assignation v, définie par p(0) = 1 et p(1) = 0, donne la
valeur 0 à la formule suivante :
(p(0) + p(1))⇒(p(0).p(1)).
Donc I définie par
pI = {0} donne aussi la
valeur 0 à cette même formule. Cet exemple montre que v et I
sont deux façons analogues de présenter une interprétation, la
deuxième étant souvent plus concise.
Théorème 4.3.44
Soit I une interprétation de A alors il existe une assignation
v de P telle que
[A]I = [A]v.
Preuve : Soient I une interprétation de A et v l'assignation
propositionnelle suivante de P dans {0, 1} : pour tout B∈P,
v(B) = [B]I. Par définition de v, l'assignation v et
l'interprétation I donnent la même valeur aux sous-formules
atomiques de A, donc la même valeur à la formule A.
Soit A une formule fermée sans symbole de fonction ni constantes,
sauf des représentations d'entiers de valeur inférieure à n. Pour
trouver une interprétation I modèle de A de domaine
{0,…, n - 1} donnant à la représentation d'un entier, la valeur de l'entier
représenté, nous procédons ainsi :
- Nous remplaçons A par sa n-expansion B.
- Dans la formule B, nous remplaçons les égalités par leur
valeur, c'est-à-dire que
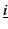 =
= 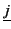 est
remplacée par 0 si i
est
remplacée par 0 si i 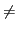 j et par 1 si i = j. De plus, nous
recommandons d'éliminer ces valeurs de vérité par les identités
x + 0 = x, x + 1 = 1, x*0 = 0, x*1 = x. Soit C la formule obtenue
après ces remplacements et simplifications.
j et par 1 si i = j. De plus, nous
recommandons d'éliminer ces valeurs de vérité par les identités
x + 0 = x, x + 1 = 1, x*0 = 0, x*1 = x. Soit C la formule obtenue
après ces remplacements et simplifications.
- Nous cherchons une assignation propositionnelle v des formules
atomiques de C, qui soit modèle de C : si une telle assignation
n'existe pas, A n'a pas de modèle, sinon l'interprétation I
déduite de v comme il est indiqué
dans le théorème 4.3.42 est modèle de A.
Prouvons la correction de cette méthode :
- Supposons qu'il n'y ait pas d'assignation propositionnelle
modèle de C, mais que A ait un modèle I. D'après le
théorème 4.3.41, I est modèle de B, donc de C, et
d'après le théorème 4.3.44, il y a une
assignation propositionnelle modèle de C. De cette contradiction,
nous déduisons que A n'a pas de modèle à n éléments.
- Supposons que l'assignation propositionnelle v soit modèle de
C. Donc, l'interprétation I construite comme il est indiqué dans
le théorème 4.3.42 est modèle de C, donc
elle est modèle de B, donc aussi d'après le
théorème 4.3.41, elle est modèle de A.
Exemple 4.3.45
Soit A la formule
∃xP(x)∧∃x¬P(x)∧∀x∀y(P(x)∧P(y)⇒x = y).
Il est clair que cette formule n'a pas de modèle à un élément car
cet élément devrait vérifier à la fois la propriété P et sa
négation. La 2-expansion de A est :
Soit A une formule fermée pouvant comporter des représentations
d'entiers de valeur inférieure à n. Comme dans le cas précédent,
nous remplaçons A par son expansion, puis nous énumérons les
choix des valeurs des symboles comme dans l'algorithme DPLL, en propageant le plus possible chacun des choix effectués.
Exemple 4.3.46
Soit A la formule
∃y P(y)⇒P(a), dont nous
cherchons un contre-modèle à 2 éléments (cela revient au même que de
trouver un modèle de la négation de A).
Exemple 4.3.47
Nous cherchons un modèle à 2 éléments des formules P(a),
∀x(P(x)⇒P(f (x))),
¬P(f (b)).
La propriété de substitution et la propriété de remplacement déjà
énoncées en logique propositionnelle (voir 1.3.1
et 1.3.10) s'étendent à la logique du premier
ordre4.3. Plus précisément l'application d'une substitution à une
formule propositionnellement valide donne une formule
valide. Par exemple soit σ la substitution propositionnelle
telle que
σ(p) = ∀x q(x). Puisque la formule
p∨¬p est valide, il en est de même de la formule
σ(p∨¬p) = ∀x q(x)∨¬∀x q(x). Le principe de
remplacement s'étend aussi avec le même énoncé de la logique
propositionnelle à la logique du premier ordre car il est déduit des
propriétés élémentaires suivantes. Pour toutes formules A et B et
toute variable x :
-
(A⇔B)
 (∀xA⇔∀xB).
(∀xA⇔∀xB).
-
(A⇔B)
 (∃xA⇔∃xB).
(∃xA⇔∃xB).
Dans cette section, nous donnons les règles permettant de simplifier
les formules de la logique du premier ordre. Remarquons que les règles
de simplifications de la logique propositionnelle sont bien entendu
encore appliquables au premier ordre.
Lemme 4.4.1
Soient A une formule et x une variable.
-
¬∀xA≡∃x¬A.
-
∀xA≡¬∃x¬A.
-
¬∃xA≡∀x¬A.
-
∃xA≡¬∀x¬A.
Prouvons les deux premières identités, les deux autres sont données en
exercice 71 :
-
-
4.4.2 Déplacement des quantificateurs
Nous donnons, sans preuve, des équivalences qui s'appliquent à toutes
les formules (avec ou sans variable libre) et qui permettent de
retrouver les lois usuelles de déplacement des quantificateurs. Nous
supposons ci-dessous que x, y sont des variables et que A, B
sont des formules.
-
∀x∀yA≡∀y∀xA.
-
∃x∃yA≡∃y∃xA.
-
∀x(A∧B)≡(∀xA∧∀xB).
-
∃x(A∨B)≡(∃xA∨∃xB).
- Soient Q un des quantificateurs
∀,∃, et o
une des opérations
∧,∨. Supposons que x ne soit pas une
variable libre de A.
-
QxA≡A,
-
Qx(AoB)≡(AoQxB).
Exemple 4.4.2
Nous éliminons de ces deux formules les
quantificateurs inutiles :
-
∀x∃xP(x)≡
-
∀x(∃xP(x)∨Q(x))≡
4.4.3 Changement de variables liées
Théorème 4.4.3
Soit Q un des quantificateurs
∀,∃.
Supposons que y soit une variable qui ne figure pas dans QxA
alors :
QxA≡QyA < x : = y >.
Exemple 4.4.4
La formule
∀x p(x, z) est équivalente à la
formule
∀y p(y, z) (d'après le théorème ci-dessus) mais
elle n'est pas équivalente à la formule
∀z p(z, z), où le
changement de variable ne respecte pas les conditions du théorème.
Définition 4.4.5 (
Formules égales à un changement près de variables liées)
Deux formules sont égales à un changement près de variables liées si
nous pouvons obtenir l'une à partir de l'autre par des remplacements
de sous-formules de la forme QxA par
QyA < x : = y > où Q
est un quantificateur et y est une variable qui ne figure pas dans
QxA. Deux formules égales à un changement près de variables liées,
sont dites aussi copies l'une de l'autre ou encore α-équivalentes.
Théorème 4.4.6
Si deux formules sont égales à un changement près de variables liées alors elles sont équivalentes.
Ce résultat est clairement une conséquence du théorème 4.4.3.
Nous n'en ferons pas la preuve, qui est longue et fastidieuse. Nous
nous contentons de suggérer cette preuve à l'aide d'un exemple.
Exemple 4.4.7
Nous montrons que les formules
∀x∃yP(x, y) et
∀y∃xP(y, x) sont égales par changement des variables
liées, au sens de la définition 4.4.3 donc sont équivalentes, en
effet :
Notre définition de l'égalité entre deux formules à un changement près
de variables liées n'est pas pratique, car la définition ne donne pas
un test. Or il est simple de voir si deux formules sont égales à un
changement près de variables liées : nous traçons des traits entre
chaque quantificateur et les variables qu'il lie et nous effaçons
les noms des variables liées. Si après cette transformation, les deux
formules deviennent identiques, c'est qu'elles sont égales à un
changement près des variables liées.
Exemple 4.4.8
Les deux formules
∀x∃yP(y, x) et
∀y∃xP(x, y) sont transformées en
∀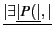 ).
).
Notons = α la relation d'égalité entre deux formules à un
changement près des variables liées. Nous donnons sans preuve des
propriétés de cette relation.
Théorème 4.4.9
Les majuscules désignent des formules et les minuscules sont des
variables.
- Soit A une formule atomique,
A = αA' si et seulement si A' = A
-
¬B = αA' si et seulement si
A' = ¬B' et
B = αB'
-
(BoC) = αA' si et seulement si
A' = (B'oC') et
B = αB' et
C = αC'. où o est l'un des
connecteurs
∧,∨,⇒,⇔.
- Si
∀xB = αA' alors
A' = ∀x'B' et pour
toute variable z absente des formules B et B', nous avons :
B < x : = z > = αB' < x' : = z >.
- Si
∃xB = αA' alors
A' = ∃x'B' et pour
toute variable z absente des formules B et B', nous avons :
B < x : = z > = αB' < x' : = z >.
- S'il existe une variable z absente des formules B et B' telle que
B < x : = z > = αB' < x' : = z >
alors
∀xB = α∀x'B' et
∃xB = α∃x'B'.
Ce théorème permet facilement d'écrire un algorithme pour tester cette
relation.
Exemple 4.4.10
Nous donnons un algorithme pour le test de
l'alpha-équivalence, ceci uniquement pour le cas où
A = ∀xB. Les données du test sont deux formules A et A'. Le résultat
est oui si
A = αA', non si
A 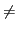 αA'.
αA'.
- Si A' n'est pas de la forme
∀x'B', alors, d'après le
point (4) du théorème, la réponse est non.
- Si
A' = ∀x'B' alors nous choisissons une variable z
quelconque absente de B et B'.
- Si
B < x : = z > = αB' < x' : = z > alors, d'après point
(6) du théorème, la réponse est oui.
- Si
B < x : = z >
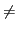 αB' < x' : = z > alors, d'après le
point (4) du théorème la réponse est non.
αB' < x' : = z > alors, d'après le
point (4) du théorème la réponse est non.




suivant: 5. Base de la
monter: II. Logique du premier
précédent: II. Logique du premier
Table des matières
Index
Benjamin Wack
2013-01-08
 , < ,≤, > ,≥
, < ,≤, > ,≥
![]() , < ,≤, > ,≥
peuvent être écrits de manière infixe, c'est-à-dire, de façon usuelle.
, < ,≤, > ,≥
peuvent être écrits de manière infixe, c'est-à-dire, de façon usuelle.
![\xymatrix{ & \Rightarrow \ar[dl] \ar[dr]& \ \forall x \ar[d] & & Q
\ar[d]\ P \ar[d] & & y\ x & & }](img100.png)
![]() et
et ![]() dont le sens est toujours fixé
respectivement à 1 et 0.
dont le sens est toujours fixé
respectivement à 1 et 0.
![]() . Par exemple l'entier 3 peut être représenté en base
10 par 3, en base 2 par 11, en chiffres romains par III, en
chiffre grec par γ. Par habitude, nous choisissons la
représentation en base 10. Dans la suite, de façon implicite,
toutes les interprétations considérées donnent à la représentation
d'un entier, la valeur de l'entier représenté.
. Par exemple l'entier 3 peut être représenté en base
10 par 3, en base 2 par 11, en chiffres romains par III, en
chiffre grec par γ. Par habitude, nous choisissons la
représentation en base 10. Dans la suite, de façon implicite,
toutes les interprétations considérées donnent à la représentation
d'un entier, la valeur de l'entier représenté.
![]() [B](I, e[x=i]). D'après le
théorème 4.3.36 et le fait que la valeur de la représentation
de l'entier i est i, nous avons :
[B](I, e[x=i]) = [B < x : =
[B](I, e[x=i]). D'après le
théorème 4.3.36 et le fait que la valeur de la représentation
de l'entier i est i, nous avons :
[B](I, e[x=i]) = [B < x : = ![]() > ](I, e). Par suite :
[∀xB](I, e) =
> ](I, e). Par suite :
[∀xB](I, e) = ![]() [B < x : =
[B < x : = ![]() > ](I, e) = [
> ](I, e) = [![]() B < x : =
B < x : = ![]() > ](I, e).
> ](I, e).
![]() et
et ![]() dont le sens est
fixé).
dont le sens est
fixé).
![]()