



suivant: 2. Résolution propositionnelle
monter: I. Logique propositionnelle
précédent: I. Logique propositionnelle
Table des matières
Index
Sous-sections
Aristote fut un des premiers à essayer de formaliser
le raisonnement en utilisant la logique des syllogismes. La logique
sert à préciser ce qu'est un raisonnement correct, indépendamment du
domaine d'application. Un raisonnement est un moyen d'obtenir une
conclusion à partir d'hypothèses données. Un raisonnement
correct ne dit rien sur la vérité des hypothèses, il dit
seulement qu'à partir de la vérité des hypothèses, nous
pouvons déduire la vérité de la conclusion. Nous commençons
l'étude de la logique par les lois de la logique propositionnelle.
La logique propositionnelle est la logique sans
quantificateurs qui s'intéresse uniquement aux lois gouvernant les
opérations logiques suivantes : la négation (¬) , la
conjonction, autrement dit le «et » (∧), la disjonction,
autrement dit le «ou » (∨), l'implication (
⇒)
et l'équivalence (
⇔). Ces opérations sont également
appelées connecteurs. La logique
propositionnelle permet de construire des raisonnements à partir de
ces connecteurs. Considérons l'exemple suivant qui comporte trois
hypothèses :
- si Pierre est grand, alors Jean n'est pas le fils de Pierre,
- si Pierre n'est pas grand, alors Jean est le fils de Pierre,
- si Jean est le fils de Pierre alors Marie est la sœur de Jean.
Nous concluons que Marie est la sœur de Jean ou Pierre est grand.
Afin de pouvoir raisonner nous extrayons la structure logique des
hypothèses. Nous désignons les phrases «Pierre est grand », «
Jean est le fils de Pierre », «Marie est la sœur de Jean » respectivement par les lettres p, j, m. Les hypothèses peuvent donc
s'écrire :
-
p⇒¬j,
-
¬p⇒j,
-
j⇒m,
et la conclusion se formalise en m∨p. Nous montrons alors que
les hypothèses impliquent la conclusion indépendamment de la nature des
énoncés p, j, m. Pour cela nous prouvons que la formule suivante est
vraie quelle que soit la vérité des propositions p, j, m.
((p⇒¬j)∧(¬p⇒j)∧(j⇒m))⇒(m∨p).
Nous débutons ce chapitre par la syntaxe
des formules logiques, c'est-à-dire, les règles permettant
d'écrire des formules. Une formule peut être vraie ou fausse, ainsi
nous devons être capable d'évaluer le sens d'une formule.
Pour cela nous introduisons le sens de chaque connecteur ainsi que le
calcul de la valeur d'une formule qui en dérive. Nous montrons alors
un résultat de compacité qui sera principalement utilisé dans la
seconde partie de ce livre. Ensuite nous présentons des équivalences remarquables utiles pour simplifier les
raisonnements logiques. D'autres méthodes permettent de simplifier
les raisonnements logiques, par exemple le remplacement et la
substitution de formule. Nous montrons ensuite comment
construire les formes normales conjonctives ou disjonctives d'une
formule en utilisant les équivalences remarquables. Ces formes
normales permettent d'exhiber facilement les modèles ou les
contre-modèles d'une formule. Nous montrons ensuite que la logique
propositionnelle est une instance d'une algèbre de Boole. Nous
introduisons la notion de fonctions booléennes. Enfin, nous présentons succinctement
l'outil BDDC1.1développé par Pascal
Raymond. Cet outil permet de
manipuler les formules propositionnelles.
1.1 Syntaxe
Avant de raisonner, nous définissons le langage que nous utilisons. Ce
langage est celui des formules construites à partir du
vocabulaire suivant :
- Les constantes :
 et
et  représentant
respectivement le vrai et le faux.
représentant
respectivement le vrai et le faux.
- Les variables : une variable est un identificateur,
avec ou sans indice, par exemple x, y1.
- Les parenthèses : ouvrante ( et
fermante ).
- Les connecteurs :
¬,∨,∧,⇒,⇔ respectivement appelés
négation, disjonction
(ou), conjonction (et),
implication et équivalence.
La syntaxe définit les règles de construction d'une formule de la
logique propositionnelle. Nous introduisons deux modes d'écriture
d'une formule, l'un strict, l'autre plus souple dans le sens qu'il
autorise plusieurs écritures d'une même formule. Cette souplesse
est obtenue grâce à l'introduction de priorités entre les
connecteurs logiques.
1.1.1 Formules strictes
Ci-dessous, nous donnons les règles de construction d'une formule
stricte à partir du vocabulaire donné précédemment.
Définition 1.1.1 (
Formule stricte)
Une formule stricte est définie de manière inductive comme
suit :
 et
et  sont des formules strictes.
sont des formules strictes.
- Une variable est une formule stricte.
- Si A est une formule stricte alors ¬A est une formule stricte.
- Si A et B sont des formules strictes et si o est une
des opérations
∨,∧,⇒,⇔ alors
(AoB) est une formule stricte.
Dans la suite, nous désignons par o tout connecteur binaire, et
nous appellons simplement formule une formule stricte. Les formules
différentes de  ,
,  et des variables sont des formules
décomposables.
et des variables sont des formules
décomposables.
Exemple 1.1.2
L'expression
(a∨(¬b∧c)) est une formule stricte
construite suivant les règles précédentes. En revanche,
a∨(¬b∧c) et
(a∨(¬(b)∧c)) ne sont pas des
formules au sens de la définition 1.1.1.
L'intérêt de la définition de formules strictes est que les
parenthèses permettent de trouver sans ambiguïté la structure des
formules. Nous représentons la structure des formules par un
arbre, où les feuilles contiennent les constantes ou
les variables et les nœuds les connecteurs logiques. Le nœud
racine est le connecteur à appliquer en dernier.
Exemple 1.1.3
La structure de la formule
(a∨(¬b∧c)) est mise en
évidence par l'arbre suivant :
Une formule peut être vue comme une liste de symbole (connecteurs,
parenthèses, variables, et constantes). Un facteur d'une telle liste
est une suite de symboles consécutifs dans la liste.
Définition 1.1.4 (Sous-formule)
Nous appelons sous-formule d'une formule
(stricte) A tout facteur de A qui est une formule (stricte).
Nous montrons que les formules sont décomposables d'une façon unique
en leurs sous-formules. Ce résultat, précisé par le
théorème 1.1.13, est évident sur les exemples. Mais la
preuve de ce résultat nécessite de nombreux résultats intermédiaires
prouvés par récurrence sur la longueur d'une formule (définie
ci-après). L'unicité de la décomposition implique que nous pouvons
identifier une formule et son arbre de décomposition. Ainsi, une
sous-formule de la formule A pourra être identifiée comme un
sous-arbre de l'arbre représentant la formule A.
Définition 1.1.6 (Longueur d'une formule)
La longueur d'une formule A
est le nombre de symboles utilisés pour écrire A, dénotée
l (A).
Si nous voyons une formule comme un mot sur le vocabulaire dont les
éléments sont les constantes, les variables, les parenthèses et les
connecteurs. Un mot sur ce vocabulaire est une suite d'éléments sur ce
vocabulaire et la longueur du mot est la longueur de la suite.
Exemple 1.1.7
Soient la formule
A = (a∨b) et
B = (A∧¬A), nous
avons l (A) = 5 et
l (B) = 4 + 5 + 5 = 14.
Lemme 1.1.8 (Équilibre des parenthèses)
Toute formule a un nombre égal de parenthèses ouvrantes et de
parenthèses fermantes.
Preuve : Par définition des formules, toute parenthèse ouvrante est associée
à une parenthèse fermante. Le lemme s'en déduit immédiatement (par
une récurrence trop simple pour mériter d'être explicitée).
Lemme 1.1.9 (Relation entre les parenthèses)
Tout préfixe d'une formule a un nombre de
parenthèses ouvrantes au moins égal à celui des parenthèses
fermantes.
Preuve : Supposons le lemme vérifié pour toute formule de longueur inférieure à n.
Soit A une formule de longueur n. Montrons que le lemme est vrai
pour A.
- Soit A une variable ou une constante. Le lemme est vérifié.
- Soit
A = ¬B où B est une formule. Un préfixe de A est
vide ou s'écrit ¬B', où B' est un préfixe de B. Par
hypothèse de récurrence, B' a un nombre de parenthèses ouvrantes
au moins égal à celui des parenthèses fermantes. Par suite il en est
de même de tout préfixe de A.
- Soit
A = (BoC) où B et C sont des formules.
Un préfixe de A est soit vide, soit s'écrit (B' où B' est un
préfixe de B, soit s'écrit
(BoC' où C' est un préfixe de
C, soit est égal à A. Examinons ces différents cas.
- Le préfixe vide a un nombre de parenthèses ouvrantes au moins
égal à celui des parenthèses fermantes.
- Par hypothèse de récurrence, B' a un nombre de parenthèses
ouvrantes au moins égal à celui des parenthèses fermantes, donc il
en est de même de (B'.
- Par hypothèse de récurrence, B et C' ont un nombre de
parenthèses ouvrantes au moins égal à celui des parenthèses fermantes,
donc il en est de même de
(BoC'.
- D'après le lemme 1.1.8, le nombre de parenthèses
ouvrantes de A est égal (donc au moins égal) au nombre des
parenthèses fermantes.
Ainsi, si le lemme est vrai pour toute formule de longueur inférieure
à n, il est vrai pour toute formule de longueur n. Donc, par
récurrence, il est vrai pour une formule de longueur quelconque.
Afin de raisonner par induction sur la structure d'une formule, nous
définissons la taille d'une formule. Nous remarquons que la taille
d'une formule correspond au nombre de connecteurs qu'elle contient.
Définition 1.1.10 (
Taille d'une formule)
La taille d'une formule A, notée
| A|, est définie inductivement par :
-
|
 | = 0 et
|
| = 0 et
| | = 0.
| = 0.
- Si A est une variable alors | A| = 0.
-
|¬A| = 1 + | A|.
-
|(AoB)| = | A| + | B| + 1.
La taille des formules définie dans la
définition 1.1.10 est une mesure utile pour prouver par
récurrence des propriétés sur les formules. La preuve du lemme
1.1.12 illustre comment écrire une preuve par récurrence sur
la taille des formules. Rappelons qu'un préfixe strict d'une formule A est un préfixe de
longueur strictement plus petite que la longueur de A.
Lemme 1.1.12 (Préfixe strict)
Tout préfixe strict d'une formule n'est pas une formule.
Preuve : Nous effectuons une preuve par induction sur la taille de la formule:
- Cas de base :
- Soit A une formule de taille 0, A est
donc soit une variable soit une constante. Le seul préfixe strict de
A est le mot vide qui n'est pas une formule.
- Induction :
- Supposons le lemme vérifié pour toute formule
de longueur inférieure à n, avec n > 0. Soit A une formule de
longueur n. Montrons que le lemme est vrai pour A.
- Soit
A = ¬B, où B est une formule. Supposons par
contradiction que A ait un préfixe strict qui soit une formule. Ce
préfixe doit s'écrire ¬B' où B' est une formule et un
préfixe strict de B. C'est impossible d'après l'hypothèse de
récurrence.
- Soit
A = (BoC) où B et C sont deux formules.
Supposons par contradiction que A ait un préfixe strict qui soit
une formule. Ce préfixe doit s'écrire
(B'oC') où B' et
C' sont des formules. La formule B est un préfixe de la formule
B' ou la formule B' est un préfixe de la formule B. Il est
impossible, d'après l'hypothèse de récurrence, que ces préfixes
soient stricts. Donc B = B'. Par suite C') est un préfixe de
C. D'après le lemme 1.1.8, C' a autant de parenthèses
ouvrantes que de fermantes. Donc C') est un préfixe de la formule
C, qui a plus de parenthèses fermantes que de parenthèses
ouvrantes, ce qui contredit le lemme 1.1.9. Donc A n'a
pas de préfixe strict qui est une formule.
Ainsi par récurrence, tout préfixe strict d'une formule n'est pas une formule.
Théorème 1.1.13
Pour toute formule A, un et un seul de ces cas se présente :
- A est
une variable,
- A est une constante,
- A s'écrit d'une unique façon sous la forme ¬B où B est
une formule,
- A s'écrit d'une unique façon sous la forme
(BoC) où B et C sont des formules.
Preuve : Puisque les vocabulaires constantes, variables, négation,
parenthèses sont disjoints, toute formule A est d'une et d'une
seule des formes variable, constante, ¬B où B est une
formule,
(BoC) où B et C sont des formules. Il suffit
de montrer l'unicité de la dernière décomposition. Supposons que
A = (BoC) = (B'oC') où
B, B', C, C' sont des formules. La
formule B est préfixe de B' ou la formule B' est préfixe de
B. D'après le lemme 1.1.12, il est impossible que ce
soient des préfixes stricts, donc B = B' et par suite C = C'.
Avec la définition de formules (strictes) nous écrivons de nombreuses
parenthèses inutiles comme les parenthèses qui entourent chaque
formule. Nous introduisons maintenant plus de souplesse dans notre
syntaxe en définissant des priorités.
Pour éviter la surabondance des parenthèses, nous définissons
les formules à priorité.
Définition 1.1.14 (
Formule à priorité)
Une formule à priorité est définie inductivement par :
 et
et  sont des formules à priorité,
sont des formules à priorité,
- une variable est une formule à priorité,
- si A est une formule à priorité alors ¬A est une formule
à priorité,
- si A et B sont des formules à priorité alors AoB est
une formule à priorité,
- si A est une formule à priorité alors (A) est une formule à
priorité.
Exemple 1.1.15
Considérons la formule
a∨¬b∧c qui est une
formule à priorité mais pas une formule.
En général, une formule à priorité n'est pas une formule (stricte). Nous
montrons dans l'exercice 2 que toute formule est une
formule à priorité. Afin de pouvoir supprimer des parenthèses sans
aucune ambiguïté nous définissons un ordre de priorité entre les
différents connecteurs.
Définition 1.1.16 (
Ordre de priorité des connecteurs)
La négation est prioritaire, puis dans l'ordre des priorités
décroissantes, nous trouvons la conjonction (∧), la
disjonction (∨), l'implication (
⇒) et l'équivalence
(
⇔).
À priorité égale, le connecteur gauche est prioritaire, sauf pour l'implication qui est associative à
droite1.2
Nous considérons qu'une formule à priorité est l'abréviation de
la formule reconstituable en utilisant les priorités. Sauf exception,
nous identifions une formule et son abréviation. Autrement dit, ce
qui nous intéresse dans une formule, ce n'est pas son écriture
superficielle, c'est sa structure, qui est mise en évidence par
la syntaxe «stricte». Ainsi la taille d'une formule à priorité sera
égale à la taille de la formule stricte dont elle est l'abréviation.
Exemple 1.1.17
Nous donnons plusieurs exemples d'abréviation de formule par une formule
à priorité :
-
a∧b∧c est l'abréviation de
-
a∧b∨c est l'abréviation de
-
a∨b∧c est l'abréviation de
Maintenant que la syntaxe est définie, nous définissons le sens des
formules.
1.2 Sens des formules
Nous cherchons à déterminer si une formule est vraie ou fausse
indépendamment des valeurs affectées à ses variables. Nous
définissons d'abord le sens des connecteurs logiques. Ensuite nous
expliquons comment calculer la valeur d'une formule et montrons le
théorème de compacité. Nous terminons cette section par la
présentation de définitions de notions de base de la logique qui
constituent le langage commun des logiciens.
1.2.1 Sens des connecteurs
Nous désignons les valeurs de vérité par 0 pour faux et par 1 pour
vrai. La constante  vaut 1 et la constante
vaut 1 et la constante  vaut 0, ce
qui nous conduit, le plus souvent, à confondre les constantes et leurs
valeurs, et à utiliser indifféremment
vaut 0, ce
qui nous conduit, le plus souvent, à confondre les constantes et leurs
valeurs, et à utiliser indifféremment  , 1 et vrai,
respectivement
, 1 et vrai,
respectivement  , 0 et faux. Le sens des connecteurs logiques
est donné par la table 1.1 qui indique les
valeurs des formules de la première ligne suivant les valeurs
assignées aux variables x et y.
, 0 et faux. Le sens des connecteurs logiques
est donné par la table 1.1 qui indique les
valeurs des formules de la première ligne suivant les valeurs
assignées aux variables x et y.
Tableau 1.1:
Table de vérité des connecteurs.
| x |
y |
¬x |
x∨y |
x∧y |
x⇒y |
x⇔y |
| 0 |
0 |
|
|
|
|
|
| 0 |
1 |
|
|
|
|
|
| 1 |
0 |
|
|
|
|
|
| 1 |
1 |
|
|
|
|
|
|
1.2.2 Valeur d'une formule
Chacun sait évaluer une formule : nous associons à chaque variable de
la formule une valeur dans l'ensemble
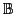 = {0, 1}. La
valeur de la formule est obtenue en remplaçant les variables par leurs
valeurs et en effectuant les opérations suivant la
table 1.1. Néanmoins, pour raisonner sur les
formules, nous définissons formellement la valeur d'une formule.
= {0, 1}. La
valeur de la formule est obtenue en remplaçant les variables par leurs
valeurs et en effectuant les opérations suivant la
table 1.1. Néanmoins, pour raisonner sur les
formules, nous définissons formellement la valeur d'une formule.
Définition 1.2.1 (
Assignation)
Une assignation est une application de l'ensemble de toutes
les variables d'une formule dans l'ensemble
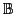 .
.
Définition 1.2.2 (Valeur d'une formule
)
Soient A une formule et v une assignation,
[A]v
dénote la valeur de la formule A dans l'assignation v. La
valeur de
[A]v est définie par récurrence
sur l'ensemble des formules. Soient A, B des formules, x une
variable et v une assignation.
-
[x]v = v(x).
-
[
 ]v = 1,
[
]v = 1,
[ ]v = 0.
]v = 0.
-
[¬A]v = 1 - [A]v autrement
dit pour calculer la valeur de ¬A, nous soustrayons à 1 la
valeur de A.
-
[(A∨B)]v = max{[A]v,[B]v}.
-
[(A∧B)]v = min{[A]v,[B]v}.
-
[(A⇒B)]v = si [A]v = 0 alors 1 sinon [B]v.
-
[(A⇔B)]v = si [A]v = [B]v alors 1 sinon 0.
D'après le théorème 1.1.13, toute formule (stricte) se
décompose de façon unique en l'un des cas ci-dessus. Ainsi l'extension
de v aux formules est une application des formules dans
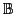 . En effet, soient 4 formules
A, A', B, B' et deux
opérations o et o' telles que
(AoB) = (A'o'B'). Par unicité de la décomposition,
A = A', B = B',o=o', donc la valeur de la formule
(AoB) est définie
uniquement par une et une seule des lignes de la définition de la
valeur. Il est clair que la valeur d'une formule ne dépend que de ses
variables et de sa structure, aussi l'évaluation d'une formule est
présentée sous la forme d'une table de vérité.
. En effet, soient 4 formules
A, A', B, B' et deux
opérations o et o' telles que
(AoB) = (A'o'B'). Par unicité de la décomposition,
A = A', B = B',o=o', donc la valeur de la formule
(AoB) est définie
uniquement par une et une seule des lignes de la définition de la
valeur. Il est clair que la valeur d'une formule ne dépend que de ses
variables et de sa structure, aussi l'évaluation d'une formule est
présentée sous la forme d'une table de vérité.
Définition 1.2.3 (
Table de vérité d'une formule)
Une table de vérité d'une formule A est un tableau qui
représente la valeur de A pour toutes les valeurs possibles des
variables de A.
Chaque ligne de la table de vérité définit une assignation pour
les variables des formules présentes dans les colonnes de la table et
chaque colonne donne la valeur d'une formule.
Exemple 1.2.4
Nous donnons la table de vérité des formules suivantes :
x⇒y, ¬x,
¬x∨y,
(x⇒y)⇔(¬x∨y) et
x∨¬y.
|
x |
y |
x⇒y |
¬x |
¬x∨y |
(x⇒y)⇔(¬x∨y) |
x∨¬y |
|
0 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
Nous listons les notions élémentaires de la logique. Nous
illustrons par des exemples et contre-exemples chacune des
définitions introduites afin d'en faire comprendre les subtilités.
Définition 1.2.5 (Formules équivalentes)
Deux formules A et B sont équivalentes si elles ont la même valeur pour toute assignation.
Exemple 1.2.6
Les colonnes des deux formules
x⇒y et
¬x∨y
sont identiques dans l'exemple 1.2.4. Ces deux formules
sont donc équivalentes. Par contre les formules
x⇒y et
x∨¬y ne sont pas équivalentes car elles n'ont pas les
mêmes tables de vérité.
Remarque 1.2.7
Nous n'utilisons pas le symbole du connecteur logique
⇔ pour dire que A et B sont équivalentes. Nous
notons que les formules A et B sont équivalentes par
A≡B ou simplement A = B si le contexte nous permet de comprendre
que le signe égal indique l'équivalence. Ainsi,
x⇒y = ¬x∨y signifie que la formule
x⇒y est
équivalente à la formule
¬x∨y.
Définition 1.2.8 (
Valide,
tautologie)
Une formule est valide si elle a la valeur 1 pour toute
assignation. Une formule valide est aussi appelée une tautologie.
Exemple 1.2.9
En regardant la table de vérité de l'exemple 1.2.4
nous obtenons que :
- la formule
(x⇒y)⇔(¬x∨y) est
valide;
- la formule
x⇒y n'est pas valide car
Notation :  A dénote le fait que la formule A est
valide. Nous pouvons écrire
A dénote le fait que la formule A est
valide. Nous pouvons écrire
 x∨¬x, car
x∨¬x, car
Propriété 1.2.10
Les formules A et B sont équivalentes si et seulement si la
formule
A⇔B est valide.
Preuve : La propriété est une conséquence de la table 1.1
et des définitions précédentes.
-
⇒
- Si les formules A et B sont équivalentes cela
signifie qu'elles ont la même table de vérité, ainsi d'après
la définition du connecteur
⇔ donnée dans la
table 1.1 la table de vérité de
A⇔B contient uniquement des 1 donc
A⇔B est
valide.
-
⇐
- Si la formule
A⇔B est valide,
nous déduisons que la table de vérité de
A⇔B
contient uniquement des 1, ainsi d'après la définition du
connecteur
⇔ donnée dans la
table 1.1 les tables de vérité de A et de B
coïncident donc les formules A et B sont équivalentes.

Définition 1.2.11 (
Modèle d'une formule)
Une assignation v qui donne la valeur 1 à une formule, est un
modèle de la formule. Nous dirons aussi que v
satisfait la formule ou que v rend vraie la formule.
Cette notion de modèle s'étend aux ensembles de formules comme suit.
Définition 1.2.13 (
Modèle d'un
ensemble de formules)
Une assignation est un modèle d'un ensemble de formules si et
seulement si elle est un modèle de chaque formule de l'ensemble.
Propriété 1.2.15
Une assignation est un modèle d'un ensemble de formules, si et
seulement si elle est un modèle de la conjonction des formules de
l'ensemble.
Preuve : La preuve est demandée dans l'exercice 11.
Exemple 1.2.16
L'ensemble de formules
{a⇒b, b⇒c}
et la formule
(a⇒b)∧(b⇒c) ont les
mêmes modèles.
Définition 1.2.17 (
Contre-Modèle)
Une assignation v qui donne la valeur 0 à une formule est un
contre-modèle de la formule. Nous dirons que v ne satisfait
pas la formule ou v rend la formule fausse.
Remarque 1.2.19 (
Contre-modèle d'un ensemble de formules)
La notion de contre-modèle s'étend aux ensembles de formules de la
même manière que la notion de modèle.
Définition 1.2.20 (
Formule
satisfaisable)
Une formule (respectivement un ensemble de formules) est
satisfaisable s'il existe une assignation qui en est un
modèle.
Définition 1.2.21 (
Formule insatisfaisable)
Une formule (respectivement un ensemble de formules) est
insatisfaisable si elle (respectivement s'il) n'est pas
satisfaisable.
Une formule (respectivement un ensemble de formules) insatisfaisable
ne possède pas de modèle. Sa table de vérité ne comporte que
des 0. La négation d'une tautologie est donc une formule
insatisfaisable.
Remarque 1.2.23
Les logiciens utilisent le mot consistant
comme synonyme de satisfaisable et
contradictoire comme synonyme
d'insatisfaisable.
Définition 1.2.24 (
Conséquence)
Soient Γ un ensemble de formules et A une formule : A est
conséquence de l'ensemble Γ d'hypothèses si tout modèle
de Γ est modèle de A. Le fait que A soit conséquence de
Γ est noté par
Γ  A.
A.
Exemple 1.2.25
D'après la table de vérité suivante, la formule
a⇒c est conséquence des
hypothèses
a⇒b et
b⇒c.
|
a |
b |
c |
a⇒b |
b⇒c |
a⇒c |
|
|
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
Remarque 1.2.26 (Validité et conséquence)
Nous notons A est valide par  A, car A est valide
si et seulement si A est conséquence de l'ensemble vide.
A, car A est valide
si et seulement si A est conséquence de l'ensemble vide.
Maintenant, nous établissons l'équivalence de la validité d'une
formule composée d'hypothèses et d'une conclusion avec la conséquence
de la conclusion à partir des hypothèses mais aussi avec
l'insatifaisabilité des hypothèses et de la négation de la conclusion.
Ces relations sont constamment utilisées dans les exercices et les
démonstrations.
Propriété 1.2.27
Soient n + 1 formules
A1,…, An, B. Soit Hn la
conjonction des formules
A1,…, An. Les trois
formulations suivantes sont équivalentes :
-
A1,…, An
 B, c'est-à-dire B est conséquence
des hypothèses
A1,…, An.
B, c'est-à-dire B est conséquence
des hypothèses
A1,…, An.
- La formule
Hn⇒B est valide.
-
Hn∧¬B est insatisfaisable.
Preuve :

Exemple 1.2.28
Nous considérons les deux formules
a⇒b et
b⇒c, nous illustrons le théorème
précédent en prouvant que
a⇒b, b⇒c  a⇒c, soit en montrant que
(a⇒b)∧(b⇒c)⇒(a⇒c) est une tautologie,
soit que
(a⇒b)∧(b⇒c)∧¬(a⇒c) est insatisfaisable. Pour cela nous donnons la table
de vérité associée à ces formules.
a⇒c, soit en montrant que
(a⇒b)∧(b⇒c)⇒(a⇒c) est une tautologie,
soit que
(a⇒b)∧(b⇒c)∧¬(a⇒c) est insatisfaisable. Pour cela nous donnons la table
de vérité associée à ces formules.
|
a |
b |
c |
a⇒b |
b⇒c |
a⇒c |
(a⇒b)∧(b⇒c)⇒(a⇒c) |
(a⇒b)∧(b⇒c)∧¬(a⇒c) |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
Nous énonçons et prouvons un résultat central de la logique « un ensemble de formules a un modèle si et seulement si tous ses
sous-ensembles finis ont un modèle ». La preuve ci-dessous de ce
résultat est écrite pour la logique propositionnelle dans le cas où
l'ensemble des variables est dénombrable. Cette
restriction nous permet de faire une preuve par récurrence sur les
entiers, en évitant l'usage de propriétés de la théorie des ensembles
ou issues de la topologie. Le théorème 1.2.30 est
utilisé dans la preuve du théorème de Herbrand
(théorème 5.1.17). Aussi, nous remettons l'étude du
paragraphe présent à ce moment.
Définition 1.2.29 (Fonction et prolongement)
Une fonction f est un triplet
f = (G, X, Y)
où G, X, Y sont des ensembles vérifiant les propriétés suivantes :
-
G⊂X×Y.
- Pour tout x∈X, il existe un et un seul y∈Y tel que
(x, y)∈G.
L'ensemble X est l'ensemble de départ ou source de f, et
l'ensemble Y est l'ensemble d'arrivée ou but de f et G est le
graphe de f. Soient deux fonctions
f = (G, X, Y) et
f' = (G', X', Y'), la fonction f est un
prolongement de f', ou une extension de
f' si nous avons les relations :
X'⊂X, Y'⊂Y et
pour tout x∈X',
f (x) = f'(x).
Théorème 1.2.30 (Compacité propositionnelle)
Un ensemble de formules propositionnelles a un modèle si et
seulement si tous ses sous-ensembles finis ont un modèle.
Preuve : Soit E un ensemble de formules propositionnelles. Soit
pi(i∈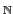 ) la liste des variables propositionnelles de
E. La condition nécessaire est triviale : si E a un modèle,
celui-ci est modèle de tous les sous-ensembles de E, en
particulier des sous-ensembles finis. Établissons la condition
suffisante. Supposons que tout sous-ensemble fini de E a un
modèle. Nous définissons une fonction δ puis nous prouvons
que δ est un modèle de E.
) la liste des variables propositionnelles de
E. La condition nécessaire est triviale : si E a un modèle,
celui-ci est modèle de tous les sous-ensembles de E, en
particulier des sous-ensembles finis. Établissons la condition
suffisante. Supposons que tout sous-ensemble fini de E a un
modèle. Nous définissons une fonction δ puis nous prouvons
que δ est un modèle de E.
- Définition de δ : soit
δi(i∈
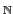 ) la suite de fonctions suivantes :
) la suite de fonctions suivantes :
- δ0 est la fonction vide, autrement dit
δ0 = ∅.
- Le domaine de δi est
{pj | 0≤j < i}.
- Soient ηi et ζi les fonctions prolongeant
δi, de domaine
{pj | 0≤j≤i} telles que
ηi(pi) = 0 et
ζi(pi) = 1. Si tout sous-ensemble fini
de E a un modèle qui est une extension de ηi alors
δi+1 = ηi sinon
δi+1 = ζi.
Soit δ la fonction de domaine
{pi | i∈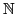 }
ainsi définie : pour tout
i∈
}
ainsi définie : pour tout
i∈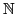 ,
δ(pi) = δi+1(pi).
,
δ(pi) = δi+1(pi).
- Propriété des fonctions δi : Soit P(i) la propriété
telle que tout sous-ensemble fini de E a un modèle qui est une
extension de δi. Par récurrence, nous prouvons que cette
propriété est vraie pour tout entier.
- la propriété P(0) est vraie, car comme
δ0 = ∅
nous retrouvons notre hypothèse initiale : tout sous-ensemble fini
de E a un modèle.
- Supposons que P(i) est vraie. Montrons P(i + 1). Nous
examinons deux cas suivant la définition de
δi+1.
-
δi+1 = ηi. Par définition de
δi+1, tout
sous-ensemble fini de E a un modèle qui est une extension de
δi+1, donc P(i + 1) est vérifiée.
-
δi+1 = ζi. Supposons que P(i + 1) ne soit pas
vérifiée. Alors, par définition de
δi+1, il existe un
sous-ensemble fini F de E, qui n'a pas de modèle qui est
une extension de ηi et, puisque P(i + 1) n'est pas vraie, il
existe un sous-ensemble fini G de E, qui n'a pas de
modèle qui soit une extension de ζi. Par suite F∪G
est un sous-ensemble fini de E, qui n'a pas de modèle qui
soit une extension de δi, ce qui contredit l'hypothèse
P(i). Par suite P(i + 1) est vérifiée.
Ainsi P(0) est vraie et pour tout i, P(i) implique
P(i + 1). Donc, par récurrence, la propriété P est vraie pour tout
entier naturel.
- Prouvons que δ est modèle de E : Soit A une formule
de E. Soit k le plus grand indice d'une variable
propositionnelle apparaissant dans la formule A. D'après la
propriété P, le singleton {A} a un modèle η qui est une
extension de
δk+1. Puisque δ et η donnent la
même valeur aux variables de A, δ est modèle de A,
formule quelconque de E. Donc δ est modèle de E.

1.2.5 Équivalences remarquables
Raisonner par équivalence c'est utiliser les propriétés de
l'équivalence (réflexivité, symétrie, transitivité), et la propriété
de remplacement d'une formule par une autre formule équivalente pour
obtenir de nouvelles équivalences à partir des équivalences déjà
prouvées ou admises. Ci-dessous, nous listons des équivalences
remarquables de la logique.
- La disjonction est :
- Associative, c'est-à-dire,
x∨(y∨z)≡(x∨y)∨z.
- Commutative, c'est-à-dire,
x∨y≡y∨x.
- 0 est l'élément neutre de la disjonction, c'est-à-dire,
0∨x≡x.
- La conjonction est :
- Associative, c'est-à-dire,
x∧(y∧z)≡(x∧y)∧z.
- Commutative, c'est-à-dire,
x∧y≡y∧x.
- 1 est l'élément neutre de la conjonction, c'est-à-dire,
1∧x≡x.
- La conjonction est distributive sur la disjonction:
x∧(y∨z)≡(x∧y)∨(x∧z).
- La disjonction est distributive sur la conjonction:
x∨(y∧z)≡(x∨y)∧(x∨z).
- Les lois de la négation :
-
x∧¬x≡ 0.
-
x∨¬x≡1 (Le
tiers-exclus).
-
¬¬x≡x.
-
¬0≡1.
-
¬1≡ 0.
- Les lois de De Morgan :
-
¬(x∧y)≡¬x∨¬y.
-
¬(x∨y)≡¬x∧¬y.
- 0 est l'élément absorbant de la conjonction :
0∧x≡ 0.
- 1 est l'élément absorbant de la disjonction :
1∨x≡1.
- idempotence de la disjonction :
x∨x≡x.
- idempotence de la conjonction :
x∧x≡x.
Les équivalences 1 à 5 se démontrent à l'aide
de tables de vérité1.3. Les équivalences 6 à
13 se déduisent des équivalences 1 à
5, comme nous le montrons dans la section 1.5.
Ci-dessous, nous donnons quelques lois de simplification qui
permettent d'alléger les raisonnements logiques.
Propriété 1.2.31 (Lois de simplification)
Pour tout x, y nous avons :
-
x∨(x∧y)≡x.
-
x∧(x∨y)≡x.
-
x∨(¬x∧y)≡x∨y.
Preuve : En utilisant les équivalences remarquables nous prouvons les trois
lois de simplification. La preuve est demandée dans
l'exercice 12.
1.3 Substitution et remplacement
Dans ce paragraphe, nous étendons l'ensemble des formules valides par
substitution et remplacement.
1.3.1 Substitution
Définition 1.3.1 (
Substitution)
Une substitution est une application de l'ensemble des
variables dans l'ensemble des formules. L'application d'une
substitution σ à une formule consiste à remplacer dans la
formule toute variable x par la formule σ(x).
Notation : Soit A une formule, nous notons Aσ ou
σ(A) l'application de la substitution σ à la formule
A.
Définition 1.3.2 (
Support d'une
substitution,
substitution à support fini)
Le support d'une substitution σ est l'ensemble des
variables x telles que
xσ 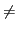 x. Une substitution σ
à support fini est notée
< x1 : = A1,…, xn : = An >,
où
A1,…, An sont des formules,
x1,…, xn sont des
variables distinctes et la substitution vérifie :
x. Une substitution σ
à support fini est notée
< x1 : = A1,…, xn : = An >,
où
A1,…, An sont des formules,
x1,…, xn sont des
variables distinctes et la substitution vérifie :
- pour i de 1 à n,
xiσ = Ai
- pour toute variable y telle que
y
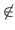 {x1,…, xn}, nous avons :
yσ = y
{x1,…, xn}, nous avons :
yσ = y
Exemple 1.3.3
Soient la formule
A = x∨x∧y⇒z∧y et
la substitution
σ = < x : = a∨b, z : = b∧c >, σ
appliquée à A donne :
Le support de σ est fini et comporte
les variables x et z.
Propriété 1.3.4
Soient A une formule, v une assignation et σ une
substitution, nous avons
[Aσ]v = [A]w où pour toute
variable x,
w(x) = [σ(x)]v.
Preuve :

Exemple 1.3.5
Soit
A = x∨y∨d une formule. Soit
σ = < x : = a∨b, y : = b∧c > une substitution. Soit v une assignation telle
que v(a) = 1, v(b) = 0, v(c) = 0, v(d )= 0. Nous avons :
Théorème 1.3.6
L'application d'une substitution à une formule valide donne une
formule valide.
Preuve : Soient A une formule valide, σ une substitution et v une
assignation quelconque. D'après la
propriété 1.3.4 :
[Aσ]v = [A]w où
pour toute variable x,
w(x) = [σ(x)]v. Puisque A est
valide,
[A]w = 1. Par suite Aσ vaut 1 dans toute
assignation, c'est donc une formule valide.
Exemple 1.3.7
Soit A la formule
¬(p∧q)⇔(¬p∨¬q). Cette formule est valide, c'est une équivalence
remarquable. Soit σ la substitution suivante :
< p : = (a∨b), q : = (c∧d ) >. La formule
La substitution est définie sur les formules, pour l'appliquer sans
erreur aux formules à priorité, il suffit que l'image, par la
substitution, de toute variable soit une variable, une constante ou
une formule entre parenthèses.
La notion de substitution ne nous permet pas de remplacer une formule
par une formule, nous introduisons la notion de remplacement à cette
fin.
Définition 1.3.8 (
Remplacement)
Soient
A, B, C, D des formules. La formule D est obtenue en
remplaçant dans C certaines occurrences de A par B, s'il
existe une formule E et une variable x telles que,
C = E < x : = A >
et
D = E < x : = B >.
Exemple 1.3.9
Considérons la formule
C = ((a⇒b)∨¬(a⇒b)).
- La formule obtenue en remplaçant toutes les occurrences de
(a⇒b) par
(a∧b) dans C est
elle est obtenue
en considérant la formule
E = (x∨¬x) et les substitutions
< x : = (a∧b) > et
< x : = (a⇒b) >.
- La formule obtenue en remplaçant la première occurrence de
(a⇒b) par
(a∧b) dans C est
elle est
obtenue en considérant la formule
E = (x∨¬(a⇒b)) et les substitutions
< x : = (a∧b) > et
< x : = (a⇒b) >.
La différence entre une substitution et un remplacement est qu'une
substitution remplace un ensemble de variables par des formules alors
qu'un remplacement remplace les occurrences de certaines formules par
une autre formule en utilisant des substitutions.
Théorème 1.3.10
Soient C une formule et D la formule obtenue en remplaçant, dans
C, des occurrences de la formule A par la formule B,
alors
(A⇔B)  (C⇔D).
(C⇔D).
Preuve : Par définition du remplacement, il existe une formule E et une
variable x telles que,
C = E < x : = A > et
D = E < x : = B >. Supposons
que v est une assignation modèle de
(A⇔B). Nous
avons donc
[A]v = [B]v. D'après la
propriété 1.3.4 :
-
[C]v = [E]w où w est identique à v sauf que
w(x) = [A]v
-
[D]v = [E]w' où w' est identique à v sauf que
w'(x) = [B]v
Puisque
[A]v = [B]v, les assignations w et w' sont
identiques, donc
[C]v = [D]v. Par suite v est modèle de
(C⇔D).
Corollaire 1.3.11
Soient C une formule et D
la formule obtenue en remplaçant, dans C, une occurrence de
la formule A par la formule B, alors
A≡B implique
C≡D.
Preuve : Si
A≡B, alors la formule
(A⇔B) est valide
(propriété 1.2.10), donc la formule
(C⇔D) également puisqu'elle est, d'après le théorème ci-dessus, la
conséquence de
(A⇔B), par suite
C≡D.
Exemple 1.3.12
Le remplacement d'une occurrence d'une formule A par une occurrence
de B est mis en évidence par des boîtes marquant ces occurrences.
- D'après théorème 1.3.10 :
p⇔q
 (p∨(
(p∨(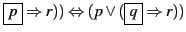 .
.
- D'après le corollaire 1.3.11 :
(¬(p∨q)⇒(
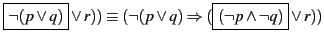 , puisque
¬(p∨q)≡(¬p∧¬q).
, puisque
¬(p∨q)≡(¬p∧¬q).
Remarque 1.3.13
Le théorème précédent et son corollaire s'appliquent aux
formules. Quand nous faisons un remplacement directement sur une
formule à priorité, nous devons nous assurer que ce remplacement
reste correct sur les formules (strictes) sous peine de commettre
des erreurs. Par exemple, considérons les deux équivalences
a∧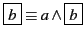 et
¬c⇒d≡c∨d. Remplaçons b à gauche par
¬c⇒d
et à droite par c∨d. Nous observons que bien que
¬c⇒d≡c∨d,
a∧¬c⇒d
et
¬c⇒d≡c∨d. Remplaçons b à gauche par
¬c⇒d
et à droite par c∨d. Nous observons que bien que
¬c⇒d≡c∨d,
a∧¬c⇒d 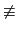 a∧c∨d, car pour a = c = d = 0, la formule de
gauche vaut 1 et celle de droite vaut 0. Ici le corollaire ne
doit pas être appliqué à l'occurrence encadrée car
a∧¬c⇒d est une abréviation de
((a∧¬c)⇒d ), donc
¬c⇒d n'apparaît pas comme
une occurrence possible de
a∧¬c⇒d.
a∧c∨d, car pour a = c = d = 0, la formule de
gauche vaut 1 et celle de droite vaut 0. Ici le corollaire ne
doit pas être appliqué à l'occurrence encadrée car
a∧¬c⇒d est une abréviation de
((a∧¬c)⇒d ), donc
¬c⇒d n'apparaît pas comme
une occurrence possible de
a∧¬c⇒d.
Nous avons défini les remplacements à partir des substitutions, nous
allons maintenant appliquer les remplacements à une formule afin de la
transformer en une formule en forme normale équivalente.
1.4 Formes Normales
Mettre une formule en forme normale consiste à la transformer en une
formule équivalente ayant des propriétés structurelles. Nous
introduisons deux notions de formes normales : la forme normale
disjonctive qui permet de mettre en évidence les modèles et la forme
normale conjonctive qui exhibe les contre-modèles. La définition de
forme normale nécessite l'introduction des concepts de littéral,
monôme et clause.
Définition 1.4.1 (
Littéral,
monôme,
clause)
- Un littéral est une variable ou la négation d'une variable.
- Un monôme est une conjonction de littéraux.
- Une clause est une disjonction de littéraux.
Nous introduisons la notion de forme normale et montrons qu'il est
toujours possible de transformer une formule en une formule
équivalente en forme normale.
Définition 1.4.3 (
Forme normale)
Une formule est en forme normale si elle n'utilise que les
opérateurs
∧,∨,¬ et que les négations sont uniquement
appliquées aux variables.
Exemple 1.4.4
La formule
¬a∨b est en forme normale, alors que la
formule
a⇒b n'est pas en forme normale bien qu'elle
soit équivalente à la première.
Nous expliquons maintenant comment transformer toute formule en une
formule en forme normale équivalente grâce à des remplacements.
Appliquer l'équivalence
A≡B à la formule C, c'est remplacer
dans C une occurrence de A par une occurrence de B : nous avons
prouvé dans le théorème 1.3.10 qu'un tel
remplacement change C en une formule équivalente. Ainsi pour
transformer une formule en une formule équivalente de forme normale,
nous appliquons les transformations suivantes :
- Élimination des équivalences : remplacer une occurrence
de
A⇔B par l'une des sous-formules :
- (a)
-
(¬A∨B)∧(¬B∨A).
- (b)
-
(A∧B)∨(¬A∧¬B).
- Élimination des implications : remplacer une occurrence
de
A⇒B par
¬A∨B.
- Déplacement des négations : remplacer une occurrence de
- (a)
-
¬¬A par A.
- (b)
-
¬(A∨B) par
¬A∧¬B.
- (c)
-
¬(A∧B) par
¬A∨¬B.
ainsi les négations ne portent que sur des variables.
En appliquant ces trois transformations dans l'ordre indiqué, il est
clair que la formule initiale a été transformée en une formule en
forme normale équivalente. Dans l'exercice 25, nous
prouvons que l'ordre des transformations n'est pas important : en
effectuant les transformations ci-dessus dans un ordre quelconque,
nous obtenons finalement une formule équivalente en forme normale.
Remarque 1.4.5
Il est par exemple recommandé de remplacer une sous-formule de la
forme
¬(A⇒B) par
A∧¬B, ce qui en fait
combine une élimination de l'implication et un déplacement de la
négation. En pratique, il est plus efficace de simplifier le plus
tôt possible de la façon suivante :
- Remplacer par 0 une conjonction qui comporte soit comporte une formule
et sa négation, soit un 0.
- Remplacer par 1 une disjonction qui comporte soit une formule
et sa négation, soit un 1.
- Remplacer ¬1 par 0 et ¬ 0 par 1.
- Enlever les 0 des disjonctions et les 1 des conjonctions.
- Appliquer les simplifications
x∨(x∧y)≡x,
x∧(x∨y)≡x,
x∨(¬x∧y)≡x∨y.
- Appliquer l'idempotence de la disjonction et de la conjonction.
La forme normale disjonctive permet de trouver facilement des modèles.
Définition 1.4.6 (
Forme normale
disjonctive)
Une formule est une forme normale disjonctive (en bref fnd)
si et seulement si elle est une disjonction (somme) de monômes.
L'intérêt des formes normales disjonctives est de mettre en évidence
les modèles.
Exemple 1.4.7
(x∧y)∨(¬x∧¬y∧z) est une fnd
composée de deux monômes, chacun d'eux nous donne un des deux
modèles possibles :
En partant d'une forme normale et en distribuant toutes les
conjonctions sur les disjonctions, nous obtenons une disjonction de
monômes. Pour cela il faut aussi savoir regrouper plusieurs
applications de la distributivité.
Exemple 1.4.8
Dans une transformation en disjonction de monômes, nous pouvons
appliquer de gauche à droite l'équivalence
(a∨b)∧(c∨d∨e)≡
La transformation par équivalence d'une formule en une disjonction de
monômes peut être utilisée pour déterminer si une formule est
valide ou non. Soit A une formule dont nous souhaitons déterminer
la validité : Nous transformons ¬A en une disjonction de
monômes équivalente à ¬A. Si
¬A = 0 alors A = 1 donc A est valide, sinon, toutes simplifications étant faites,
¬A est égal à une disjonction de monômes non nuls, qui
nous donnent des modèles de ¬A, donc des contre-modèles de A.
Exemple 1.4.9
Soit
A = (p⇒(q⇒r))⇒(p∧q⇒r). Déterminons si A est valide par transformation de
¬A en disjonction de monômes.
Exemple 1.4.10
Soit
A = ((a⇒b)∧c)∨(a∧d ). Déterminer si A est
valide par transformation de ¬A en disjonction de monômes.
La forme normale conjonctive permet d'exhiber facilement des
contre-modèles.
Définition 1.4.11 (
Forme normale conjonctive)
Une formule est une forme normale conjonctive (en bref fnc)
si et seulement si elle est une conjonction (produit) de clauses.
L'intérêt des formes normales conjonctives est de mettre en évidence
des contre-modèles.
Par convention, nous considérons que 0 et 1 sont des disjonctions
de monômes et des conjonctions de clauses. Nous appliquons la
distributivité (inhabituelle) de la disjonction sur la conjonction,
autrement dit nous remplaçons toute sous-formule
A∨(B∧C) par
(A∨B)∧(A∨C), et toute sous-formule
(B∧C)∨A par
(B∨A)∧(C∨A).
La transformation par équivalence d'une formule en une conjonction de
clauses de littéraux peut aussi être utilisée pour déterminer si
une formule est valide ou non. Soit A une formule dont nous
souhaitons déterminer la validité : Nous transformons A en une
conjonction de clauses équivalente à A. Si
A = 1 alors A est valide, sinon, toutes simplifications étant
faites, A est égale à une conjonction de clauses
non égales à 1, et chacune de ces disjonctions nous donne un
contre-modèle de A.
1.5 Algèbre de Boole
Cette notion fut introduite par le mathématicien britannique George
Boole au milieu du XIXe
siècle. Elle permet notamment de traduire les propositions en
équations (généralement, cette écriture est plus concise). Nous
rappelons d'abord la définition d'une algèbre de Boole. Nous
déduisons alors que la logique propositionnelle est une algèbre de
Boole. Ensuite nous prouvons certaines propriétés usuelles des
algèbres de Boole. Nous terminons cette section en présentant la
notion de dualité.
La définition d'algèbre de Boole donnée ci-dessous est minimale en nombre d'axiomes.
Définition 1.5.1
Une algèbre de Boole est un ensemble
d'au moins deux éléments, 0, 1, et trois opérations, complément
(le complément de x est noté
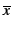 ), somme (+) et
produit (.), qui vérifient les axiomes suivants :
), somme (+) et
produit (.), qui vérifient les axiomes suivants :
- la somme est :
- associative :
x + (y + z) = (x + y) + z,
- commutative :
x + y = y + x,
- 0 est élément neutre de la somme : 0 + x = x,
- le produit est :
- associatif :
x.(y.z) = (x.y).z,
- commutatif : x.y = y.x,
- 1 est élément neutre du produit : 1.x = x,
- le produit est distributif sur la somme :
x.(y + z) = (x.y) + (x.z),
- la somme est distributive sur le produit :
x + (y.z) = (x + y).(x + z),
- les lois de la négation :
-
x +
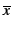 = 1,
= 1,
-
x.
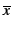 = 0.
= 0.
Attention, le fait que la distributivité de la somme sur le
produit n'est pas usuelle rend son application propice aux erreurs.
Comme indiqué précédemment dans la sous-section 1.2.5,
nous pouvons prouver en utilisant des tables de vérité que la logique
propositionnelle vérifie l'ensemble des axiomes d'une algèbre de
Boole. Ainsi nous pouvons considérer la logique propositionnelle
comme la plus petite algèbre de Boole, car elle contient deux
éléments. De ce fait, nous pouvons utiliser les notations
booléennes (plus condensées) en lieu et place des notations
propositionnelles, comme indiqué dans la table de correspondance
donnée dans la figure 1.1. Nous conseillons de les
utiliser pour effectuer de gros calculs. Par ailleurs, observez que
ces notations sont fréquemment utilisées dans le domaine du matériel.
Figure 1.1:
Correspondance entre l'algèbre de Boole et
la logique propositionnelle.
| notations logiques |
notations booléennes |
| ¬a |
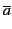 |
|
a∧b |
a.b |
| a∨b |
a + b |
|
a⇒b |
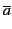 + b + b |
|
a⇔b |
a.b + (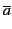 . .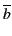 ) ou
(a + ) ou
(a + 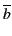 ).( ).(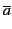 + b) + b) |
|
Remarque 1.5.2 (Conventions d'écriture)
- Parfois, la négation est utilisée à la place du
complémentaire. Par exemple, - a dénote
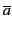 et - (a + b)
représente
et - (a + b)
représente
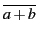 .
.
- Afin de permettre l'omission du point, dans les notations
booléennes, les variables sont souvent dénotées par une seule
lettre (avec ou sans indice). Ainsi lorsque a et b sont des
variables, des formules entre parenthèses ou sous une barre de
négation, nous abrégeons a.b en ab suivant une pratique usuelle
en mathématiques.
- Enfin l'équivalence de deux formules est systématiquement notée
avec le symbole = au lieu du symbole ≡.
Il est important de noter que la logique propositionnelle n'est pas
l'unique algèbre de Boole. Par exemple, l'ensemble
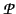 (X)
des sous-ensembles d'un ensemble X est une algèbre de Boole, comme
nous l'indique la mise en correspondance des opérateurs ensemblistes
avec leur désignation dans l'algèbre de Boole dans la
figure 1.2.
(X)
des sous-ensembles d'un ensemble X est une algèbre de Boole, comme
nous l'indique la mise en correspondance des opérateurs ensemblistes
avec leur désignation dans l'algèbre de Boole dans la
figure 1.2.
Figure 1.2:
Correspondance entre l'algèbre de Boole et
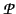 (X).
(X).
| Algèbre de Boole |
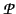 (X) (X) |
| 1 |
X |
| 0 |
∅ |
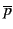 |
X - p |
| p + q |
p∪q |
| p.q |
p∩q |
|
Puisque les lois de simplification sont déduites des lois de l'algèbre
de Boole, comme nous allons le montrer dans la suite, elles sont
vérifiées dans toute algèbre de Boole. En particulier dans l'algèbre
de Boole
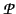 (X) nous avons
A∪(A∩B) = A. Une
preuve dans l'algèbre de Boole est une suite d'égalités,
permettant de passer d'une formule à une autre formule
équivalente en utilisant les axiomes ou simplifications de
l'algèbre de Boole.
(X) nous avons
A∪(A∩B) = A. Une
preuve dans l'algèbre de Boole est une suite d'égalités,
permettant de passer d'une formule à une autre formule
équivalente en utilisant les axiomes ou simplifications de
l'algèbre de Boole.
Nous présentons certaines des propriétés qui découlent de la
définition de l'algèbre de Boole et qui sont couramment utilisées
dans les raisonnements. Pour raccourcir les preuves de ces propriétés,
nous utilisons implicitement l'associativité et la commutativité de la
somme et du produit.
Propriété 1.5.3
Dans une algèbre de Boole, pour tout x, il y a un et un seul y tel
que x + y = 1 et xy = 0, autrement dit la négation est unique.
Preuve : Il y a un élément y vérifiant x + y = 1 et xy = 0, c'est
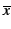 d'après les axiomes de l'algèbre de Boole. Montrons qu'il est
unique. Raisonnons par contradiction, supposons qu'il n'est pas
unique, nous avons donc qu'il existe y et z deux éléments
distincts tels que x + y = 1, xy = 0, x + z = 1, et xz = 0. Nous
considérons u = xy + z. Puisque xy = 0, nous avons : u = z. Par
distributivité de la somme sur le produit, nous avons :
u = (x + z)(y + z). Puisque x + z = 1 et que 1 est l'élément neutre du
produit, nous avons : u = y + z. Nous concluons donc que z = y + z.
En considérant v = xz + y et échangeant les rôles de y et z, nous
obtenons de façon analogue y = y + z. Par suite y = z, ce qui
prouve donc l'unicité de la négation.
d'après les axiomes de l'algèbre de Boole. Montrons qu'il est
unique. Raisonnons par contradiction, supposons qu'il n'est pas
unique, nous avons donc qu'il existe y et z deux éléments
distincts tels que x + y = 1, xy = 0, x + z = 1, et xz = 0. Nous
considérons u = xy + z. Puisque xy = 0, nous avons : u = z. Par
distributivité de la somme sur le produit, nous avons :
u = (x + z)(y + z). Puisque x + z = 1 et que 1 est l'élément neutre du
produit, nous avons : u = y + z. Nous concluons donc que z = y + z.
En considérant v = xz + y et échangeant les rôles de y et z, nous
obtenons de façon analogue y = y + z. Par suite y = z, ce qui
prouve donc l'unicité de la négation.
Preuve :
-
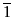 = 0.
= 0.
-
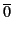 = 1.
= 1.
-
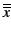 = x.
= x.
- Idempotence du produit : x.x = x.
- Idempotence de la somme : x + x = x.
- 1 est élément absorbant de la somme : 1 + x = 1.
- 0 est élément absorbant du produit : 0.x = 0.
- Lois de De Morgan :

1.5.3 Dualité
La présentation de l'algèbre de Boole montre que 0 et 1, la somme et
le produit jouent des rôles symétriques. Dans ce paragraphe, nous
nous restreignons aux formules qui s'écrivent avec ces symboles plus
la négation. La duale d'une formule est obtenue en échangeant
les produits et les sommes ainsi que les 0 et les 1.
Définition 1.5.5 (Formule duale
)
Nous notons A* la formule duale de A, définie de
manière inductive par :
- x* = x,
- 0* = 1,
- 1* = 0,
-
(¬A)* = (¬A*),
-
(A∨B)* = (A*∧B*),
-
(A∧B)* = (A*∨B*).
Théorème 1.5.7
En logique propositionnelle, si deux formules sont équivalentes, alors
leurs duales sont aussi équivalentes.
Preuve : Voir exercice 29.
Corollaire 1.5.8
En logique propositionnelle, si une formule est valide, sa duale est
contradictoire.
Preuve : Voir exercice 29.
En fait les résultats ci-dessus sont vrais non seulement pour la
logique propositionnelle, qui est une algèbre de Boole à deux
éléments, mais aussi pour toute algèbre de Boole. Nous définissons
l'égalité de deux formules dans une algèbre de Boole.
Définition 1.5.9 (
Égalité booléenne)
Une formule A est égale à une formule B dans une algèbre de
Boole si :
- A et B sont syntaxiquement identiques,
- A et B constituent les deux membres d'un axiome de l'algèbre de Boole,
- B est égale à A (l'égalité est symétrique),
- il existe une formule C telle que A est égale à C et C est égale à
B (transitivité de l'égalité),
- il existe deux formules C et D telles que C est égale à,
D et B est obtenue en remplaçant dans A une occurrence de C
par D.
Théorème 1.5.10
Si deux formules sont égales dans une algèbre de Boole, alors leurs
duales sont aussi égales.
Preuve : La preuve est similaire a l'exercice 29 en remplaçant
l'algèbre booléenne à deux éléments par une algèbre booléenne
quelconque.
1.6 Fonctions booléennes
Nous regardons maintenant nos formules comme des fonctions
mathématiques sur le domaine
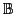 = {0, 1}. Nous
définissons formellement ce qu'est une fonction booléenne, puis nous
revisitons les formes normales conjonctives et disjonctives avec ce
formalisme. Remarquons que les fonctions booléennes sont des notions
utilisées en cryptologie par exemple dans la construction de
chiffrements symétriques (le chiffrement One-Time-Pad, un des
chiffrements les plus sûrs est basé sur la fonction booléenne du
«ou-exclusif »).
= {0, 1}. Nous
définissons formellement ce qu'est une fonction booléenne, puis nous
revisitons les formes normales conjonctives et disjonctives avec ce
formalisme. Remarquons que les fonctions booléennes sont des notions
utilisées en cryptologie par exemple dans la construction de
chiffrements symétriques (le chiffrement One-Time-Pad, un des
chiffrements les plus sûrs est basé sur la fonction booléenne du
«ou-exclusif »).
Définition 1.6.1 (
Fonction booléenne)
Une fonction booléenne f est une fonction dont les arguments et le
résultat sont dans le domaine
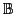 = {0, 1}.
= {0, 1}.
f :
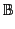 n
n→
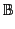
Exemple 1.6.2
Nous donnons des exemples et contre-exemples de fonctions booléennes :
- La fonction
f :
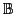 →
→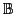 : f (x) = ¬x
: f (x) = ¬x
- La fonction
f :
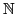 →
→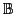 : f (x) = x mod 2
: f (x) = x mod 2
- La fonction
f :
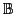 →
→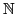 : f (x) = x + 1
: f (x) = x + 1
- La fonction
f :
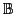 ×
×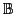 →
→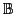 : f (x, y) = ¬(x∧y)
: f (x, y) = ¬(x∧y)
Grâce aux fonctions booléennes, nous sommes capables à partir des
valeurs de vérité d'une formule de reconstruire la somme de
monômes correspondante. Pour toute variable x, nous posons
x0 = 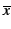 et x1 = x.
et x1 = x.
Théorème 1.6.3
Soit f une fonction booléenne à n arguments. Cette fonction est
représentée à l'aide de n variables
x1,…, xn. Soit A la
formule suivante :
A =
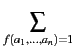 x1a1
x1a1…
xnan.
Les ai sont des valeurs booléennes et A est la somme des monômes
x1a1…xnan tels que
f (a1,…, an) = 1. Par
convention, si la fonction f vaut toujours 0 alors A = 0.
Pour toute assignation v telle que
v(x1) = a1,…, v(xn) = an, nous avons
f (a1,…, an) = [A]v. En omettant
la distinction entre une variable et sa valeur, ce résultat s'écrit
plus brièvement :
f (x1,…xn) = A.
Avant de lire la preuve, nous conseillons d'examiner
l'exemple 1.6.4. La preuve n'est que la généralisation de
cet exemple avec des notations, qui peuvent sembler complexes.
Preuve : Soit v une assignation quelconque.

1.6.2 Fonctions booléennes et produit de clauses
Nous effectuons le même raisonnement pour la forme duale.
Théorème 1.6.5
Soit f une fonction booléenne à n arguments. Cette fonction est
représentée à l'aide de n variables
x1,…, xn. Soit A
la formule suivante :
Les ai sont des valeurs
booléennes et A est le produit des clauses
x1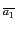 + … + xn
+ … + xn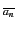 telles que
f (a1,…, an) = 0.
Par convention si la fonction f vaut toujours 1 alors A = 1.
telles que
f (a1,…, an) = 0.
Par convention si la fonction f vaut toujours 1 alors A = 1.
Pour toute assignation v telle que
v(x1) = a1,…, v(xn) = an, nous avons
f (a1,…, an) = [A]v. En
omettant la distinction entre une variable et sa valeur, ce
résultat s'écrit plus brièvement :
f (x1,…, xn) = A.
Preuve :

1.7 L'outil BDDC
BDDC (Binary Decision Diagram based
Calculator) est un outil pour la manipulation de formules
propositionnelles développé par Pascal Raymond et disponible à
l'adresse suivante :
Cet outil est une «calculette propositionnelle
» basée sur les diagrammes de décision
binaires. Ces diagrammes
permettent d'avoir une représentation interne des formules logiques sous la forme
d'un graphe orienté acyclique ayant pour propriété d'être canonique. Cette calculette offre notamment la possibilité :
- d'évaluer si une formule est une tautologie,
- d'évaluer si une formule a un modèle,
- de transformer une formule en forme normale conjonctive,
- de transformer une formule en forme normale disjonctive,
- ...
Ainsi, il est possible d'utiliser BDDC pour résoudre plusieurs des
exercices proposés ci-après, parmi lesquels les exercices
8 à 16 et 23 à 24.




suivant: 2. Résolution propositionnelle
monter: I. Logique propositionnelle
précédent: I. Logique propositionnelle
Table des matières
Index
Benjamin Wack
2013-01-08
![]()
![]()
![]() vaut 1 et la constante
vaut 1 et la constante ![]() vaut 0, ce
qui nous conduit, le plus souvent, à confondre les constantes et leurs
valeurs, et à utiliser indifféremment
vaut 0, ce
qui nous conduit, le plus souvent, à confondre les constantes et leurs
valeurs, et à utiliser indifféremment ![]() , 1 et vrai,
respectivement
, 1 et vrai,
respectivement ![]() , 0 et faux. Le sens des connecteurs logiques
est donné par la table 1.1 qui indique les
valeurs des formules de la première ligne suivant les valeurs
assignées aux variables x et y.
, 0 et faux. Le sens des connecteurs logiques
est donné par la table 1.1 qui indique les
valeurs des formules de la première ligne suivant les valeurs
assignées aux variables x et y.
![]() = {0, 1}. La
valeur de la formule est obtenue en remplaçant les variables par leurs
valeurs et en effectuant les opérations suivant la
table 1.1. Néanmoins, pour raisonner sur les
formules, nous définissons formellement la valeur d'une formule.
= {0, 1}. La
valeur de la formule est obtenue en remplaçant les variables par leurs
valeurs et en effectuant les opérations suivant la
table 1.1. Néanmoins, pour raisonner sur les
formules, nous définissons formellement la valeur d'une formule.
![]() . En effet, soient 4 formules
A, A', B, B' et deux
opérations o et o' telles que
(AoB) = (A'o'B'). Par unicité de la décomposition,
A = A', B = B',o=o', donc la valeur de la formule
(AoB) est définie
uniquement par une et une seule des lignes de la définition de la
valeur. Il est clair que la valeur d'une formule ne dépend que de ses
variables et de sa structure, aussi l'évaluation d'une formule est
présentée sous la forme d'une table de vérité.
. En effet, soient 4 formules
A, A', B, B' et deux
opérations o et o' telles que
(AoB) = (A'o'B'). Par unicité de la décomposition,
A = A', B = B',o=o', donc la valeur de la formule
(AoB) est définie
uniquement par une et une seule des lignes de la définition de la
valeur. Il est clair que la valeur d'une formule ne dépend que de ses
variables et de sa structure, aussi l'évaluation d'une formule est
présentée sous la forme d'une table de vérité.
![]() ) la liste des variables propositionnelles de
E. La condition nécessaire est triviale : si E a un modèle,
celui-ci est modèle de tous les sous-ensembles de E, en
particulier des sous-ensembles finis. Établissons la condition
suffisante. Supposons que tout sous-ensemble fini de E a un
modèle. Nous définissons une fonction δ puis nous prouvons
que δ est un modèle de E.
) la liste des variables propositionnelles de
E. La condition nécessaire est triviale : si E a un modèle,
celui-ci est modèle de tous les sous-ensembles de E, en
particulier des sous-ensembles finis. Établissons la condition
suffisante. Supposons que tout sous-ensemble fini de E a un
modèle. Nous définissons une fonction δ puis nous prouvons
que δ est un modèle de E.
![]()
![]()
![]()
![]() (X)
des sous-ensembles d'un ensemble X est une algèbre de Boole, comme
nous l'indique la mise en correspondance des opérateurs ensemblistes
avec leur désignation dans l'algèbre de Boole dans la
figure 1.2.
(X)
des sous-ensembles d'un ensemble X est une algèbre de Boole, comme
nous l'indique la mise en correspondance des opérateurs ensemblistes
avec leur désignation dans l'algèbre de Boole dans la
figure 1.2.
![]() (X) nous avons
A∪(A∩B) = A. Une
preuve dans l'algèbre de Boole est une suite d'égalités,
permettant de passer d'une formule à une autre formule
équivalente en utilisant les axiomes ou simplifications de
l'algèbre de Boole.
(X) nous avons
A∪(A∩B) = A. Une
preuve dans l'algèbre de Boole est une suite d'égalités,
permettant de passer d'une formule à une autre formule
équivalente en utilisant les axiomes ou simplifications de
l'algèbre de Boole.
![]() d'après les axiomes de l'algèbre de Boole. Montrons qu'il est
unique. Raisonnons par contradiction, supposons qu'il n'est pas
unique, nous avons donc qu'il existe y et z deux éléments
distincts tels que x + y = 1, xy = 0, x + z = 1, et xz = 0. Nous
considérons u = xy + z. Puisque xy = 0, nous avons : u = z. Par
distributivité de la somme sur le produit, nous avons :
u = (x + z)(y + z). Puisque x + z = 1 et que 1 est l'élément neutre du
produit, nous avons : u = y + z. Nous concluons donc que z = y + z.
En considérant v = xz + y et échangeant les rôles de y et z, nous
obtenons de façon analogue y = y + z. Par suite y = z, ce qui
prouve donc l'unicité de la négation.
d'après les axiomes de l'algèbre de Boole. Montrons qu'il est
unique. Raisonnons par contradiction, supposons qu'il n'est pas
unique, nous avons donc qu'il existe y et z deux éléments
distincts tels que x + y = 1, xy = 0, x + z = 1, et xz = 0. Nous
considérons u = xy + z. Puisque xy = 0, nous avons : u = z. Par
distributivité de la somme sur le produit, nous avons :
u = (x + z)(y + z). Puisque x + z = 1 et que 1 est l'élément neutre du
produit, nous avons : u = y + z. Nous concluons donc que z = y + z.
En considérant v = xz + y et échangeant les rôles de y et z, nous
obtenons de façon analogue y = y + z. Par suite y = z, ce qui
prouve donc l'unicité de la négation.![]()
![]()
![]() + c))* =
+ c))* =
![]()
![]()
![]()
![]() = {0, 1}. Nous
définissons formellement ce qu'est une fonction booléenne, puis nous
revisitons les formes normales conjonctives et disjonctives avec ce
formalisme. Remarquons que les fonctions booléennes sont des notions
utilisées en cryptologie par exemple dans la construction de
chiffrements symétriques (le chiffrement One-Time-Pad, un des
chiffrements les plus sûrs est basé sur la fonction booléenne du
«ou-exclusif »).
= {0, 1}. Nous
définissons formellement ce qu'est une fonction booléenne, puis nous
revisitons les formes normales conjonctives et disjonctives avec ce
formalisme. Remarquons que les fonctions booléennes sont des notions
utilisées en cryptologie par exemple dans la construction de
chiffrements symétriques (le chiffrement One-Time-Pad, un des
chiffrements les plus sûrs est basé sur la fonction booléenne du
«ou-exclusif »).
![]() et x1 = x.
et x1 = x.
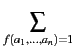 x1a1…xnan.
x1a1…xnan.
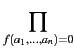 x1
x1