



suivant: 3. Déduction Naturelle
monter: I. Logique propositionnelle
précédent: 1. Logique propositionnelle
Table des matières
Index
Sous-sections
2. Résolution propositionnelle
Les tables de vérité et les transformations en sommes
de monômes ou produits de clauses permettent de répondre aux questions
: une formule est-elle valide ? et un raisonnement est-il correct ?
Cependant le temps de réponse de ces méthodes augmente
exponentiellement avec le nombre de variables. Pour illustrer cela,
considérons la conséquence suivante :
a⇒
b,
b⇒
c,
c⇒
d,
d⇒
e,
e⇒
f,
f⇒
g,
g⇒
h,
h⇒
i,
i⇒
j 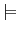 a
a⇒
j
En utilisant une table de vérité il faut tester
210 = 1024
lignes. Or par déduction, en utilisant la
transitivité de l'implication, nous savons immédiatement que le
raisonnement ci-dessus est correct. Ainsi, en logique
propositionnelle, les déductions peuvent s'avérer très utile, voir
nécessaire lorsque la taille du problème à traiter est importante.
Nous étudions maintenant un système de déduction très simple. Dans ce
système, les hypothèses et les formules déduites ne sont pas des
formules quelconques mais des clauses,
c'est-à-dire des disjonctions de littéraux. De plus, le système
comporte une seule règle appelée la
résolution.
Nous introduisons d'abord la méthode de résolution inventée en
1965 par J. Alan
Robinson [23] dans le
cadre plus général de la recherche de preuve au premier ordre. Nous
présentons ensuite une procédure pour calculer tous les résolvants
possibles, c'est-à-dire toutes les applications possibles de la règle
de résolution : la stratégie
complète. Puis, nous
étudions l'algorithme DPLL, proposé dans
les années soixante par Martin
Davis, Hilary
Putnam,
George W. Logemann et
Donald W. Loveland [10,9]. En utilisant la notion de
résolution, des méthodes de simplifications et le branchement/retour
arrière, cet algorithme prouve efficacement si une formule a un modèle
ou non. Bien qu'inventé il y a plus de quarante ans, il est toujours à
la base de la plupart des solveurs SAT complets actuels. Notons que dans ce chapitre nous adoptons la
notation booléenne plus concise.
Nous souhaitons prouver que a + c est une conséquence de a + b et
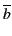 + c, c'est-à-dire
a + b,
+ c, c'est-à-dire
a + b, 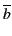 + c
+ c  a + c. En
utilisant la propriété 1.2.27, il suffit de démontrer que la
formule
(a + b).(
a + c. En
utilisant la propriété 1.2.27, il suffit de démontrer que la
formule
(a + b).(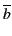 + c)⇒(a + c) est valide. Pour
cela, nous pouvons utiliser une table de vérité (8 lignes) ou alors
une simplification de formules comme dans
l'exercice 13. Ces deux méthodes sont
fastidieuses même pour des formules aussi simples (3 variables
uniquement). En utilisant la règle de résolution présentée dans ce
chapitre, nous déduisons directement la clause a + c à partir des deux
clauses a + b et
+ c)⇒(a + c) est valide. Pour
cela, nous pouvons utiliser une table de vérité (8 lignes) ou alors
une simplification de formules comme dans
l'exercice 13. Ces deux méthodes sont
fastidieuses même pour des formules aussi simples (3 variables
uniquement). En utilisant la règle de résolution présentée dans ce
chapitre, nous déduisons directement la clause a + c à partir des deux
clauses a + b et
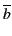 + c.
+ c.
Nous donnons maintenant la définition de la résolution et certaines
propriétés utiles qui en dérivent. Nous prouvons ensuite la cohérence et la complétude pour la réfutation de notre
système basé sur la déduction. La cohérence nous permet d'affirmer que
si une clause C est obtenue par résolution à partir d'un ensemble
Γ de clauses alors elle en est conséquence, c'est-à-dire tout
modèle de Γ est modèle de C. La complétude pour la réfutation
nous permet d'affirmer que si  est conséquence de Γ,
autrement dit si Γ est insatisfaisable, alors
est conséquence de Γ,
autrement dit si Γ est insatisfaisable, alors  peut être
retrouvé par résolution à partir de Γ.
peut être
retrouvé par résolution à partir de Γ.
Dans un premier temps nous introduisons les notions nécessaires à la
définition de la résolution. Nous rappelons que les notions de clauses
et littéraux sont définies dans la section 1.4 du chapitre
précédent (page ![[*]](crossref.png) ). Comme nous le verrons dans la
suite deux clauses qui ont le même ensemble de littéraux jouent le
même rôle dans la résolution. Aussi, nous définissons deux clauses
égales comme étant deux clauses avec le même ensemble de littéraux.
). Comme nous le verrons dans la
suite deux clauses qui ont le même ensemble de littéraux jouent le
même rôle dans la résolution. Aussi, nous définissons deux clauses
égales comme étant deux clauses avec le même ensemble de littéraux.
Définition 2.1.1 (
Éléments d'une
clause, clauses égales et sous-clauses)
- Un littéral est élément d'une clause, s'il est élément de
l'ensemble des littéraux de la clause.
- Une clause A est incluse dans une clause B, si tous
les littéraux de la clause A sont éléments de la clause B. Dans
ce cas, A est une sous-clause de B.
- Deux clauses sont égales si elles ont le même ensemble de
littéraux.
Exemple 2.1.2
Nous illustrons les notions introduites par des exemples simples :
Notation : Nous notons s(A) l'ensemble des littéraux
de la clause A. Par convention  est la clause vide et
s(
est la clause vide et
s( ) = ∅.
) = ∅.
Dans l'exercice 37 nous demandons de formaliser ce
qu'est une clause et son ensemble de littéraux. Nous introduisons la
notion de littéral complémentaire, noté Lc
pour un littéral L, afin de manipuler dans nos raisonnements
uniquement des littéraux. En effet, la négation ne suffit pas car
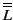 est équivalent à L mais n'est pas
un littéral : un littéral est une variable ou la négation
d'une variable mais la double négation d'une variable n'est pas un
littéral.
est équivalent à L mais n'est pas
un littéral : un littéral est une variable ou la négation
d'une variable mais la double négation d'une variable n'est pas un
littéral.
Définition 2.1.4 (
Littéral complémentaire)
Notons Lc le littéral complémentaire d'un littéral L,
défini par :
- Si L est une variable, Lc est la négation de L.
- Si L est la négation d'une variable, Lc est obtenue en
enlevant la négation de L.
Nous présentons le calcul de résolvant entre deux clauses, ce qui
constitue l'unique règle du système de résolution.
Définition 2.1.6 (
Résolvant)
Soient A et B deux clauses. La clause C est un résolvant de A
et B si et seulement s'il y a un littéral L tel que
L∈s(A),
Lc∈s(B) et
s(C) = (s(A) - {L})∪(s(B) - {Lc}). Nous
utilisons la représentation suivante lorsque C est un résolvant de
A et B :
Si la clause C est un résolvant de A et B, alors nous disons que
C est engendrée par A et B, et que A et B sont les
parents de la clause C.
Propriété 2.1.8
Si l'un des parents d'un résolvant est valide, le résolvant est valide ou contient l'autre parent.
Preuve : Cette preuve est demandée dans l'exercice 40.
Étant données deux clauses A et B, la formule A + B n'est
pas une clause si l'un des deux opérandes de la disjonction est la
clause vide. Par exemple  + p n'est pas une clause, bien que
les deux opérandes de la disjonction soient des clauses.
Aussi nous introduisons un nouvel opérande,
+ p n'est pas une clause, bien que
les deux opérandes de la disjonction soient des clauses.
Aussi nous introduisons un nouvel opérande,  , afin de
combiner la disjonction et l'élimination de
, afin de
combiner la disjonction et l'élimination de  . Cet opérande va
nous permettre de simplifier la définition de résolvant.
. Cet opérande va
nous permettre de simplifier la définition de résolvant.
Ajouter le littéral L à la clause C, c'est construire
C L. Munis de cette définition, nous pouvons reformuler plus
simplement la règle de résolution.
L. Munis de cette définition, nous pouvons reformuler plus
simplement la règle de résolution.
Définition 2.1.10 (
Résolvant)
Soient A et B deux clauses. La clause C est un
résolvant de A et B si et seulement s'il y a un littéral
L tel que :
- L est élément de la clause A, Lc est élément de la clause
B
- C est égale à la clause
A'
 B' où
A' = A - {L} est obtenue en enlevant L de A et
B' = B - {Lc} est
obtenue en enlevant Lc de B.
B' où
A' = A - {L} est obtenue en enlevant L de A et
B' = B - {Lc} est
obtenue en enlevant Lc de B.
La combinaison de résolutions successives permet de générer de nouvelles
clauses. Une clause issue de ces résolvants sera une preuve par
résolution de cette clause à partir d'un ensemble de clauses.
Définition 2.1.11 (Preuve
)
Soient Γ un ensemble de clauses et C une clause. Une
preuve de C à partir de Γ est une liste de clauses qui
se termine par C. Toute clause de la preuve est égale à un élément
de Γ ou est un résolvant de deux clauses la précédant dans la
preuve. La clause C est déduite de Γ, notée
Γ  C, s'il y a une preuve de C à partir de Γ.
C, s'il y a une preuve de C à partir de Γ.
Nous pouvons aussi voir une preuve comme un arbre dont les
feuilles sont les hypothèses et dont les sommets internes sont obtenus
par construction des résolvants.
Définition 2.1.13 (Taille de preuve
)
Une preuve P de C à partir d'un ensemble de clauses Γ est
de taille n si elle contient n lignes.
La taille de la preuve donnée dans
l'example 2.1.12 est 8, ce qui n'est pas
forcément intuitif sur la représentation en arbre. Nous utiliserons
les deux propriétés énoncées ci-dessous souvent de manière implicite
dans les preuves.
Preuve : Demandée dans l'exercice 39.

La cohérence de la résolution signifie que si une clause C est
obtenue après une à plusieurs applications de la règle de résolution à
un ensemble de clauses Γ alors tout modèle de Γ est
aussi modèle de C (autrement dit, C est une conséquence de
Γ). La première partie de la preuve consiste à démontrer la
cohérence d'une application de la règle de résolution
(théorème 2.1.15). Nous généralisons ensuite par induction dans
le théorème 2.1.16.
Théorème 2.1.15 (Cohérence de la règle de résolution)
Si C est un résolvant de A et B alors
A, B  C.
C.
Preuve : Supposons que C soit un résolvant de A et B. Par définition
il y a un littéral L tel que
L∈s(A), Lc∈s(B), s(C) = (s(A) - {L})∪(s(B) - {Lc}). Soit v une assignation
modèle de A et B, c'est-à-dire, [A]v = 1 et [B]v = 1. Montrons
que v est modèle de C. Nous distinguons deux cas possibles :

Théorème 2.1.16 (Cohérence de la déduction)
Soient Γ un ensemble de clauses et C une clause. Si
Γ  C alors
Γ
C alors
Γ  C.
C.
Preuve : Supposons que
Γ  C. Par définition, il existe une
preuve P de C à partir de Γ. Supposons que pour toute
preuve de D à partir de Γ, plus courte que P, nous
avons
Γ
C. Par définition, il existe une
preuve P de C à partir de Γ. Supposons que pour toute
preuve de D à partir de Γ, plus courte que P, nous
avons
Γ  D. Montrons que
Γ
D. Montrons que
Γ  C. Nous
avons deux cas possibles :
C. Nous
avons deux cas possibles :

2.1.3 Complétude pour la réfutation
La complétude pour la réfutation est la propriété suivante : si
Γ est un ensemble insatisfaisable de clauses, alors il y a une
preuve de la clause vide à partir de Γ. Nous montrons dans la
suite de cette section la complétude pour la
réfutation lorsque Γ est un ensemble fini de clauses.
Nous prouvons la complétude réfutationnelle par récurrence sur le
nombre de variables. Pour cela, nous construisons à partir de Γ
deux ensembles de clauses contenant tous deux une variable en
moins. Plus précisément, nous construisons les ensembles
Γ[L : = 1] et
Γ[L : = 0] en assignant un littéral L de Γ à
vrai et à faux, respectivement. Nous étudions ensuite les propriétés
de ces deux ensembles par rapport à Γ (lemmes 2.1.22 et
2.1.23). Ces propriétés seront utilisées lors du pas de
récurrence.
Définition 2.1.18 (
Γ[
L : = 1]
)
Soient Γ un ensemble de clauses et L un
littéral.
Γ[L : = 1] est l'ensemble de clauses obtenu en
supprimant les clauses dont L est élément et en enlevant Lc des
autres clauses. Nous posons
Γ[L : = 0] = Γ[Lc : = 1].
Γ[L : = x] est égal à l'ensemble de clauses obtenu en donnant
à L la valeur x (x = 0 ou x = 1) et en simplifiant le résultat
obtenu.
Exemple 2.1.19
Soit Γ l'ensemble de clauses
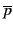 + q,
+ q,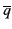 + r, p + q, p + r. Nous avons :
+ r, p + q, p + r. Nous avons :
-
Γ[p : = 1] =
-
Γ[p : = 0] =
Afin de donner une intuition de comment calculer
Γ[p : = 1] et
Γ[p : = 0], nous considérons le produit de clauses suivant
(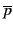 + q)(
+ q)(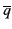 + r)(p + q)(p + r) et observons :
+ r)(p + q)(p + r) et observons :
-
(
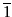 + q)(
+ q)(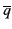 + r)(1 + q)(1 + r) =
+ r)(1 + q)(1 + r) =
-
(
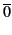 + q)(
+ q)(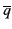 + r)(0 + q)(0 + r) =
+ r)(0 + q)(0 + r) =
Nous notons v[L : = 1] l'assignation qui donne à L la valeur 1, à
Lc la valeur 0 et ne change pas la valeur des autres littéraux.
Définition 2.1.20 (
v[
L : = 1]
)
Soit une assignation v, l'assignation v[L : = 1] est l'assignation
identique à v sauf éventuellement pour x la variable de L. Si
L = x alors
v[L : = 1](x) = 1, si
L = 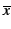 alors
v[L : = 1](x) = 0.
alors
v[L : = 1](x) = 0.
Nous posons
v[L : = 0] = v[Lc : = 1]. La propriété suivante se déduit du
fait que si Γ a un modèle v, alors v donne soit la valeur
1 soit la valeur 0 au littéral L.
Propriété 2.1.21
Soient Γ un ensemble de clauses et L un littéral. Γ
a un modèle si et seulement si
Γ[L : = 1] ou
Γ[L : = 0] a
un modèle.
Preuve :
-
⇒
- Supposons que l'assignation v soit modèle de
Γ. Nous considérons deux cas selon la valeur de L dans
cette assignation.
- Supposons que v donne à L la valeur 1 et montrons que v
est modèle de
Γ[L : = 1]. Soit C une clause de
Γ[L : = 1]. Il y a dans Γ une clause C' telle que C
est obtenue en enlevant Lc de C'. Puisque v est modèle de
Γ, v est modèle de C' donc d'un littéral qui n'est pas
Lc (car Lc vaut 0 dans cette assignation). Par suite v est
modèle de C. Puisque C est une clause quelconque de
Γ[L : = 1], v est modèle de
Γ[L : = 1].
- Supposons que v donne à L la valeur 0. Nous nous ramenons au
cas précédent en échangeant L et Lc et nous montrons que v
est modèle de
Γ[L : = 0].
-
⇐
- Nous considérons deux cas suivant que
Γ[L : = 1] ou
Γ[L : = 0] a un modèle.
- Supposons que l'assignation v soit modèle de
Γ[L : = 1].
Montrons que v[L : = 1] est modèle de Γ. Soit C une clause
de Γ.
- Supposons que L soit un littéral de C, alors v[L : = 1] est
modèle de C puisque cette assignation donne à L la valeur 1.
- Supposons que L ne soit pas un littéral de C. Alors il y a une
clause C' élément de
Γ[L : = 1] telle que C' est obtenue en
enlevant Lc de C. La variable de L n'est pas une variable de
C'. Par suite v et v[L : = 1] donnent la même valeur à
C'. Puisque v est modèle de
Γ[L : = 1], v est modèle de
C' donc v[L : = 1] est modèle de C'. Puisque C' est incluse
dans C, v[L : = 1] est modèle de C.
Puisque C est une clause quelconque de Γ, v[L : = 1] est
modèle de Γ.
- Supposons que l'assignation v est modèle de
Γ[L : = 0]. Par une preuve analogue, nous montrons que v[L : = 0]
est modèle de Γ.

Lemme 2.1.22
Soient Γ un ensemble de clauses, C une clause et L un
littéral. Si
Γ[L : = 1]  C alors
Γ
C alors
Γ  C ou
Γ
C ou
Γ  C
C Lc.
Lc.
Rappel : L'opération  est introduite dans
la définition 2.1.9.
est introduite dans
la définition 2.1.9.
Preuve : Partant d'une preuve de C à partir de
Γ[L : = 1], nous obtenons
une preuve de C ou de
C Lc à partir de Γ en
ajoutant le littéral Lc aux clauses où nous l'avions
enlevé. Formalisons cette ébauche de preuve. Supposons que
Γ[L : = 1]
Lc à partir de Γ en
ajoutant le littéral Lc aux clauses où nous l'avions
enlevé. Formalisons cette ébauche de preuve. Supposons que
Γ[L : = 1]  C. Il y a une preuve P de C à partir de
Γ[L : = 1]. Supposons que pour toute preuve de D à partir de
Γ[L : = 1], plus courte que P, nous avons
Γ
C. Il y a une preuve P de C à partir de
Γ[L : = 1]. Supposons que pour toute preuve de D à partir de
Γ[L : = 1], plus courte que P, nous avons
Γ  D ou
Γ
D ou
Γ  D
D Lc. Nous avons deux cas possibles :
Lc. Nous avons deux cas possibles :
- C est élément de
Γ[L : = 1]. Donc il y a une clause C'
élément de Γ telle que
s(C') = s(C) ou
s(C') = s(C)∪{Lc}. Examinons ces deux cas.
- Supposons
s(C') = s(C).
Par définition des preuves,
Γ
 C.
C.
- Supposons
s(C') = s(C)∪{Lc}.
Nous avons
s(C') = s(C
 Lc) donc par définition des preuves,
Γ
Lc) donc par définition des preuves,
Γ  C
C Lc.
Lc.
- C est résolvant de 2 clauses A et B précédant C dans la preuve P.
Donc par hypothèse de récurrence :
-
Γ
 A ou
Γ
A ou
Γ  A
A Lc.
Lc.
-
Γ
 B ou
Γ
B ou
Γ  B
B Lc.
Lc.
Ce qui donne 4 cas à examiner.
- Supposons
Γ
 A et
Γ
A et
Γ  B.
Puisque C
est résolvant de A et B, d'après la propriété 2.1.14, nous
avons
Γ
B.
Puisque C
est résolvant de A et B, d'après la propriété 2.1.14, nous
avons
Γ  C.
C.
- Supposons
Γ
 A et
Γ
A et
Γ  B
B Lc.
Puisque C est résolvant de A et B, il existe M tel que M∈A et Mc∈B et
s(C) = (s(A) - {M})∪(s(B) - {Mc}). Aucune clause de
Γ[L : = 1] ne comporte le littéral
Lc. Donc B qui en est déduite, ne comporte pas le littéral
Lc (voir exercice 41) et par suite
Lc
Lc.
Puisque C est résolvant de A et B, il existe M tel que M∈A et Mc∈B et
s(C) = (s(A) - {M})∪(s(B) - {Mc}). Aucune clause de
Γ[L : = 1] ne comporte le littéral
Lc. Donc B qui en est déduite, ne comporte pas le littéral
Lc (voir exercice 41) et par suite
Lc 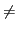 Mc.
Par conséquent
(s(B) - {Mc})∪{Lc} = (s(B)∪{Lc}) - {Mc} = s(B
Mc.
Par conséquent
(s(B) - {Mc})∪{Lc} = (s(B)∪{Lc}) - {Mc} = s(B Lc) - {Mc}. Nous avons donc
s(C
Lc) - {Mc}. Nous avons donc
s(C Lc) = (s(A) - {M})∪(s(B) - {Mc})∪{Lc} = (s(A) - {M})∪(s(B
Lc) = (s(A) - {M})∪(s(B) - {Mc})∪{Lc} = (s(A) - {M})∪(s(B Lc) - {Mc}). D'après la dernière égalité,
C
Lc) - {Mc}). D'après la dernière égalité,
C Lc est un résolvant de A et
B
Lc est un résolvant de A et
B Lc. Donc par la
propriété 2.1.14,
Γ
Lc. Donc par la
propriété 2.1.14,
Γ  C
C Lc.
Lc.
- Supposons
Γ
 A
A Lc et
Γ
Lc et
Γ  B,
en échangeant ci-dessus le rôle de A et B, nous obtenons
Γ
B,
en échangeant ci-dessus le rôle de A et B, nous obtenons
Γ  C
C Lc.
Lc.
- Supposons
Γ
 A
A Lc et
Γ
Lc et
Γ  B
B Lc, comme ci-dessus nous obtenons
Γ
Lc, comme ci-dessus nous obtenons
Γ  C
C Lc.
Lc.
Par suite dans les quatre cas, nous avons
Γ  C ou
Γ
C ou
Γ  C
C Lc.
Lc.

Lemme 2.1.23
Soient Γ un ensemble de clauses, C une clause et L un
littéral. Si
Γ[L : = 0]  C alors
Γ
C alors
Γ  C ou
Γ
C ou
Γ  C
C L.
L.
Preuve : Supposons
Γ[L : = 0]  C. Puisque
Γ[L : = 0] = Γ[Lc : = 1] et que Lcc = L, d'après le lemme
2.1.22 nous avons
Γ
C. Puisque
Γ[L : = 0] = Γ[Lc : = 1] et que Lcc = L, d'après le lemme
2.1.22 nous avons
Γ  C ou
Γ
C ou
Γ  C
C L.
L.
Théorème 2.1.24
Soit Γ un ensemble fini de clauses. Si Γ est
insatisfaisable alors
Γ 
 .
.
Preuve : Supposons que Γ est insatisfaisable. Soit n le nombre de
variables de Γ. Nous montrons que
Γ 
 par
récurrence sur n. Supposons que pour tout ensemble Δ de
clauses insatisfaisable avec moins de n variables, nous avons
Δ
par
récurrence sur n. Supposons que pour tout ensemble Δ de
clauses insatisfaisable avec moins de n variables, nous avons
Δ 
 .
.
- Cas de base :
- Supposons que n soit nul. Donc
Γ = ∅ ou
Γ = {
 }. Le premier cas est impossible,
car l'ensemble vide est valide (toute assignation en est
modèle). Donc
Γ = {
}. Le premier cas est impossible,
car l'ensemble vide est valide (toute assignation en est
modèle). Donc
Γ = { } et par suite
Γ
} et par suite
Γ 
 .
.
- Induction :
- Supposons que n soit non nul. Soit x une
variable figurant dans Γ. D'après la
propriété 2.1.21,
Γ[x : = 0] et
Γ[x : = 1] sont
insatisfaisables. Puisque la variable x ne figure pas dans ces
deux ensembles de clauses, l'hypothèse de récurrence s'applique,
donc :
Γ[x : = 0]

 et
Γ[x : = 1]
et
Γ[x : = 1] 
 . Des
lemmes 2.1.22 et 2.1.23, nous déduisons soit
Γ
. Des
lemmes 2.1.22 et 2.1.23, nous déduisons soit
Γ 
 , soit
Γ
, soit
Γ 
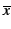 et
Γ
et
Γ  x. Dans le premier cas, la preuve est terminée. Dans le deuxième
cas, puisque
x. Dans le premier cas, la preuve est terminée. Dans le deuxième
cas, puisque  est un résolvant de
est un résolvant de
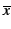 et x, nous avons
également
Γ
et x, nous avons
également
Γ 
 .
.

Corollaire 2.1.25
Soit Γ un ensemble fini de clauses. Γ est
insatisfaisable si et seulement si
Γ 
 .
.
Preuve : Ce corollaire est une conséquence immédiate du lemme ci-dessus et de
la remarque faite au début du paragraphe 2.1.3.
2.1.4 Réduction d'un ensemble de clauses
Réduire un ensemble de clauses, c'est lui enlever les clauses valides
et les clauses contenant une autre clause de l'ensemble. Un
ensemble de clauses est réduit s'il n'est plus réductible.
Définition 2.1.26 (
Ensemble de clauses réduit)
Un ensemble de clauses est réduit s'il ne contient aucune
clause valide et aucune clause n'est incluse dans une autre clause.
Exemple 2.1.27
La réduction de l'ensemble de clauses
{p + q + 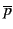 , p + r, p + r +
, p + r, p + r + 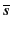 , r + q} donne l'ensemble réduit :
, r + q} donne l'ensemble réduit :
Propriété 2.1.28
Un ensemble de clauses E est équivalent à l'ensemble de clauses
réduit obtenu à partir de E.
Preuve :

Définition 2.1.29 (Clause minimale pour la déduction
)
Soit
Γ un ensemble de clauses. Une clause minimale pour la
déduction de Γ est une clause non valide déduite de Γ
et ne contenant strictement aucune clause déduite de Γ.
Exemple 2.1.30
Considérons l'ensemble de clauses
Γ = {a + 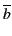 , b + c + d} la clause a + c + d est minimale pour
la déduction. Par contre si on rajoute la clause
, b + c + d} la clause a + c + d est minimale pour
la déduction. Par contre si on rajoute la clause
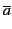 + c
à Γ alors a + c + d n'est pas minimale car nous pouvons
déduire c + d qui est inclus dans la clause a + c + d.
+ c
à Γ alors a + c + d n'est pas minimale car nous pouvons
déduire c + d qui est inclus dans la clause a + c + d.
L'algorithme de la stratégie complète, présenté dans le paragraphe
suivant, construit, à partir d'un ensemble Γ de clauses,
l'ensemble des clauses minimales pour la déduction de Γ.
Propriété 2.1.31
Soit Θ l'ensemble des clauses minimales pour la déduction de l'ensemble de clauses
Γ.
L'ensemble Γ est insatisfaisable si et seulement si
 ∈Θ.
∈Θ.
Preuve :
- Supposons
 ∈Θ, alors
Γ
∈Θ, alors
Γ 
 , donc
par cohérence de la résolution, Γ est insatisfaisable.
, donc
par cohérence de la résolution, Γ est insatisfaisable.
- Supposons Γ insatisfaisable, par complétude de la
résolution,
Γ

 . Par suite
. Par suite  est minimale pour
la déduction de Γ, donc
est minimale pour
la déduction de Γ, donc
 ∈Θ.
∈Θ.

Définition 2.1.32 (Clause minimale pour la conséquence
)
Soit Γ un ensemble de clauses. Une clause minimale pour
la conséquence de Γ est une clause non valide conséquence
de Γ et ne contenant strictement aucune clause
conséquence de Γ.
Exemple 2.1.33
Considérons l'ensemble de clauses
Γ = {a + d,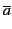 + b,
+ b,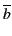 + c}. La clause d + c est minimale pour la
conséquence de Γ.
+ c}. La clause d + c est minimale pour la
conséquence de Γ.
- Conséquence :
- d + c est une conséquence de Γ car dans
tout modèle de Γ soit d est vrai soit c est vrai. Pour
s'en convaincre essayons de construire un modèle où d et c sont
faux. Dans ce cas pour satisfaire la première et la dernière clause
de Γ, il faut que a = 1 et b = 0 dans le modèle ce qui rend
faux la seconde clause de Γ.
- Minimalité :
- Il existe des modèles de Γ qui ne sont pas
modèles de d (respectivement c) : a = 1, d = 0, c = 1 et b = 1
(respectivement a = 0, d = 1, c = 0 et b = 0).
Nous montrons ci-dessous, qu'une clause est minimale pour la déduction
d'un ensemble de clauses si et seulement si elle est minimale pour la
conséquence de ce même ensemble de clauses.
Propriété 2.1.34
Soit Γ un ensemble de clauses. Pour toute clause C non valide, conséquence de Γ,
il existe une sous-clause de C déduite de Γ.
Preuve : Soient C une clause non valide, conséquence de Γ et
Γ' = Γ∪{Lc | L∈C}. Une assignation v
est modèle de Γ' si et seulement si v est modèle de
Γ et n'est pas modèle de C, donc, puisque C est
conséquence de Γ, Γ' est insatisfaisable. De plus, par
complétude réfutationnelle, nous obtenons
Γ' 
 .
.
Nous montrons la propriété (P) suivante : pour toute clause D
déduite de Γ' :
- Soit D est le complémentaire d'un littéral de C.
- Soit il existe une clause E telle que
E⊂C et D∪E est déductible de Γ.
En appliquant la propriété (P) à la clause vide qui est déduite de
Γ', il en résulte qu'il existe une sous-clause de C déduite
de Γ.
La preuve de la propriété (P) est une preuve par induction sur la
longueur n de la preuve par résolution de D. Le cas de base pour
n = 0 est immédiat, car
D∈Γ. Supposons que pour toute preuve
de longueur inférieure à n la propriété (P) soit vraie. Nous
distinguons deux cas :
- Supposons
D∈Γ', donc soit D est le complémentaire
d'un littéral de C, soit
D∈Γ et par suite D est
déduite de Γ, donc la propriété (P) est vraie.
- Supposons
D
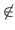 Γ'. Donc D est le résolvant de deux
clauses E et F ayant une preuve de longueur inférieure à n.
Par suite, il existe un littéral L avec
L∈E, Lc∈F et
D = (E - {L})∪(F - {Lc}). Puisque C n'est pas valide, la
résolution ne peut pas être appliquée à deux clauses qui sont des
littéraux complémentaires de ceux de C. Donc au moins l'une des
clauses E, F n'est pas un littéral complémentaire d'un littéral de
C. Supposons que cette clause non complémentaire d'un littéral de
C soit la clause E. Par hypothèse de récurrence, il existe une
clause G telle que
G⊂C et E∪G est déductible de
Γ. Nous distinguons deux cas, suivant que F soit ou ne soit
pas le complémentaire d'un littéral de C.
Γ'. Donc D est le résolvant de deux
clauses E et F ayant une preuve de longueur inférieure à n.
Par suite, il existe un littéral L avec
L∈E, Lc∈F et
D = (E - {L})∪(F - {Lc}). Puisque C n'est pas valide, la
résolution ne peut pas être appliquée à deux clauses qui sont des
littéraux complémentaires de ceux de C. Donc au moins l'une des
clauses E, F n'est pas un littéral complémentaire d'un littéral de
C. Supposons que cette clause non complémentaire d'un littéral de
C soit la clause E. Par hypothèse de récurrence, il existe une
clause G telle que
G⊂C et E∪G est déductible de
Γ. Nous distinguons deux cas, suivant que F soit ou ne soit
pas le complémentaire d'un littéral de C.
- F est le complémentaire d'un littéral de C. Dans ce cas, F
est le littéral Lc et
D = E - {L}. De plus, comme L∈E,
nous avons
L
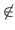 D et
E = D∪{L}.
Ensuite, puisque
G⊂C, nous avons
(G - {L})⊂C.
Puisque
E∪G = D∪{L}∪G et
F = {Lc} sont
déductibles de Γ (par hypothèse de récurrence) et
D∪(G - {L}) est un résolvant de E∪G et F, nous pouvons
conclure que
D∪(G - {L}) est déductible de Γ.
Ainsi, la propriété est vérifiée pour D.
D et
E = D∪{L}.
Ensuite, puisque
G⊂C, nous avons
(G - {L})⊂C.
Puisque
E∪G = D∪{L}∪G et
F = {Lc} sont
déductibles de Γ (par hypothèse de récurrence) et
D∪(G - {L}) est un résolvant de E∪G et F, nous pouvons
conclure que
D∪(G - {L}) est déductible de Γ.
Ainsi, la propriété est vérifiée pour D.
- F n'est pas le complémentaire d'un littéral de C. Par
hypothèse de récurrence, il existe une clause H telle que
H⊂C et F∪H est déductible de Γ. Puisque
G⊂C et
H⊂C, nous avons
G∪H⊂C.
Puisque E∪G ainsi que F∪H sont déductibles de Γ
et que D est un résolvant de E et F, alors
D∪(G∪H)
est un résolvant de E∪G et de F∪H et par suite est
aussi déductible de Γ. Donc la propriété (P) est vérifiée
pour D.

Remarquons que cette propriété généralise la propriété de la
complétude réfutationnelle, si la clause vide est conséquence d'un
ensemble de clauses, alors elle en est déduite.
Théorème 2.1.35
Soit Γ un ensemble de clauses. Une clause est minimale pour la déduction de Γ
si et seulement si elle est minimale pour la conséquence de Γ.
Preuve : Nous effectuons une preuve par double implications.
-
⇒
- Soit C une clause minimale pour la déduction de Γ. Par
cohérence de la résolution,
Γ
 C. Nous supposons que
C ne soit pas minimale pour la conséquence et cherchons une
contradiction. Dans ce cas, il existerait une clause D,
sous-clause stricte de C et conséquence de Γ. Puisque C
n'est pas valide, D aussi n'est pas valide, d'après la propriété
2.1.34, il existerait E sous-clause de D déduite de
Γ. Donc, contrairement à l'hypothèse, C ne serait pas
minimale pour la déduction. Par suite, C est minimale pour la
conséquence.
C. Nous supposons que
C ne soit pas minimale pour la conséquence et cherchons une
contradiction. Dans ce cas, il existerait une clause D,
sous-clause stricte de C et conséquence de Γ. Puisque C
n'est pas valide, D aussi n'est pas valide, d'après la propriété
2.1.34, il existerait E sous-clause de D déduite de
Γ. Donc, contrairement à l'hypothèse, C ne serait pas
minimale pour la déduction. Par suite, C est minimale pour la
conséquence.
-
⇐
- Soit C minimale pour la conséquence de Γ.
Puisque C n'est pas valide, d'après la propriété
2.1.34, il existe D, une sous-clause de C déduite de
Γ. Par cohérence de la résolution, D est conséquence de
Γ. Et puisque C est minimale, D = C, donc C est déduite
de Γ. Nous supposons que C ne soit pas minimale pour la
déduction. Il existerait D, sous-clause stricte de C, déduite de
Γ. Par cohérence de la résolution, D serait conséquence de
Γ. Donc, contrairement à l'hypothèse, C ne serait pas
minimale pour la conséquence. Par suite, C est minimale pour la
déduction.

2.2 Stratégie complète
Pour savoir si un ensemble fini Γ de clauses est
contradictoire, il y a une méthode simple mais peu efficace :
construire toutes les clauses que nous pouvons déduire de
Γ. D'après le corollaire 2.1.25,
Γ est contradictoire si et seulement si la clause vide a été
construite. Il faut préciser ce que nous entendons par construire
toutes les clauses déduites de Γ. Si nous considérons comme
différentes les clauses qui s'écrivent différemment, deux clauses ont
une infinité de résolvants. Par exemple les clauses
p + 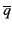 et r + q ont comme résolvants la clause p + r mais aussi les clauses
r + p, p + r + p,
p + … + p + r + ... + r. Donc l'ensemble des clauses
déduites de Γ est infini. Aussi, il faut, comme précédemment,
considérer comme égales deux clauses, qui ont le même ensemble de
littéraux (voir définition 2.1.1) : avec cette
définition de l'égalité de deux clauses, l'ensemble des
résolvants de deux clauses est fini ainsi que l'ensemble des clauses
déduites de Γ. Supposons que l'ensemble des littéraux de
Γ ait n éléments, comme les clauses déduites de Γ ne
comportent que des littéraux de Γ (voir
exercice 41), il y a donc au plus 2n clauses
déduites de Γ. Pour simplifier la suite, comme ci-dessus, nous
confondons une clause et son ensemble de littéraux.
et r + q ont comme résolvants la clause p + r mais aussi les clauses
r + p, p + r + p,
p + … + p + r + ... + r. Donc l'ensemble des clauses
déduites de Γ est infini. Aussi, il faut, comme précédemment,
considérer comme égales deux clauses, qui ont le même ensemble de
littéraux (voir définition 2.1.1) : avec cette
définition de l'égalité de deux clauses, l'ensemble des
résolvants de deux clauses est fini ainsi que l'ensemble des clauses
déduites de Γ. Supposons que l'ensemble des littéraux de
Γ ait n éléments, comme les clauses déduites de Γ ne
comportent que des littéraux de Γ (voir
exercice 41), il y a donc au plus 2n clauses
déduites de Γ. Pour simplifier la suite, comme ci-dessus, nous
confondons une clause et son ensemble de littéraux.
Soit Γ un ensemble de clauses. Pour obtenir l'ensemble des
clauses minimales déduites de Γ, on construit deux suites
d'ensembles de clauses
Δi(i≥0) et
Θi(i≥0) en
s'arrêtant au premier indice k tel que
Δk = ∅.
- Δ0 est obtenu en réduisant Γ et Θ0 est
l'ensemble vide.
-
Δi+1 est obtenu de la façon suivante
- Nous construisons l'ensemble des résolvants entre les clauses de
Δi et celles de
Δi∪Θi puis nous réduisons
cet ensemble.
- Nous enlevons de cet ensemble de résolvants, les clauses qui
contiennent une clause de
Δi∪Θi.
-
Θi+1 est obtenu en enlevant de l'ensemble
Δi∪Θi les clauses qui contiennent une clause de
Δi+1.
Nous illustrons notre algorithme par deux exemples.
Exemple 2.2.1
Nous appliquons
l'algorithme à l'ensemble de clauses
a + b + 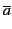 , a + b, a + b + c, a +
, a + b, a + b + c, a + 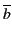 ,
,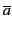 + b,
+ b,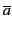 +
+  .
L'algorithme effectue alors le calcul suivant. L'ensemble
Δ0 comprend les clauses :
.
L'algorithme effectue alors le calcul suivant. L'ensemble
Δ0 comprend les clauses :
L'ensemble Θ0 est vide. L'algorithme calcule les résolvants
non valides suivants :
Donc l'ensemble Δ1 comprend les mêmes clauses que nous
numérotons de 5 à 8.
L'ensemble Θ1 est
L'ensemble Δ2 comprend la clause :
L'ensemble Θ2 est
L'ensemble Δ3 est
L'ensemble Θ3 est égal à
Nous notons que
l'algorithme a construit la preuve suivante :
Nous pouvons utiliser la représentation ci-dessous sous
forme de tableau représentant la construction de ces ensembles.
|
k |
Δk |
Θk |
Δk∪Θk |
Résolvants de Δk et
Δk∪Θk |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
Comme le montre cet exemple, les clauses de Δi ont des preuves
de hauteur i, et celles de Θi des preuves de hauteur
inférieure à i.
Nous montrons que l'algorithme se termine et qu'il est correct,
c'est-à-dire que l'ensemble Θk est l'ensemble des clauses
minimales déduites de Γ. D'après la
propriété 2.1.31, Γ est insatisfaisable
si et seulement si la clause vide est élément de Θk.
Soit n le nombre de littéraux de Γ. Les clauses éléments des
Δi sont des clauses déduites de Γ, donc, comme nous
l'avons rappelé ci-dessus, elles ne comportent que des littéraux de
Γ. Par suite, l'ensemble
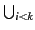 Δi comprend
au plus 2n clauses. D'après l'algorithme, les ensembles Δi
sont non vides pour i < k. Nous montrons ci-dessous que ces
ensembles sont disjoints. Par conséquent
k≤2n + 1, autrement dit
l'algorithme s'arrête.
Δi comprend
au plus 2n clauses. D'après l'algorithme, les ensembles Δi
sont non vides pour i < k. Nous montrons ci-dessous que ces
ensembles sont disjoints. Par conséquent
k≤2n + 1, autrement dit
l'algorithme s'arrête.
Preuve : Nous effectuons une preuve par induction.
- Pour i = 0 la propriété est triviale car
Θ0 = ∅.
- Supposons la propriété vraie au rang i et montrons qu'elle
reste vraie au rang i + 1. Soit
C∈
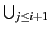 Δj. Montrons que C contient une clause de
Δi+1∪Θi+1. Nous examinons tous les cas
possibles pour C.
Δj. Montrons que C contient une clause de
Δi+1∪Θi+1. Nous examinons tous les cas
possibles pour C.
-
C∈Δi+1. Donc C contient une clause de
Δi+1∪Θi+1.
-
C∈
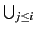 Δj. Par hypothèse de récurrence,
C contient une clause
D∈Δi∪Θi. Nous
distinguons deux situations pour D.
Δj. Par hypothèse de récurrence,
C contient une clause
D∈Δi∪Θi. Nous
distinguons deux situations pour D.
-
D∈Θi+1. Donc C contient une clause de
Δi+1∪Θi+1.
-
D
 Θi+1. Par construction de
Θi+1,
puisque
D∈Δi∪Θi et que
D
Θi+1. Par construction de
Θi+1,
puisque
D∈Δi∪Θi et que
D  Θi+1, c'est que D contient une clause de
Δi+1. Or C contient D, donc C contient aussi une
clause de
Δi+1∪Θi+1.
Θi+1, c'est que D contient une clause de
Δi+1. Or C contient D, donc C contient aussi une
clause de
Δi+1∪Θi+1.

Preuve : Nous effectuons une récurrence sur les ensembles Δj avec
0≤j≤i et i≤k.
- Case de base :
- Si i = 0, il n'y a qu'un seul ensemble, donc la
propriété est vérifiée.
- Récurrence :
- Soit i < k. Supposons que tous les ensembles
Δj où j≤i sont disjoints entre eux.
Montrons que
Δi+1 est disjoint de ces ensembles.
Soit
C∈Δi+1. Supposons, au contraire, que
C∈ Δj. D'après la propriété précédente, C
inclut une clause de
Δi∪Θi. Donc par
construction de
Δi+1,
C
Δj. D'après la propriété précédente, C
inclut une clause de
Δi∪Θi. Donc par
construction de
Δi+1,
C  Δi+1,
contradiction. Par suite,
C
Δi+1,
contradiction. Par suite,
C 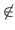
 Δj.
Δj.

Nous montrons ci-dessous que l'ensemble Θk est équivalent à Γ.
Propriété 2.2.5
Pour tout i < k, les ensembles
Δi∪Θi et
Δi+1∪Θi+1 sont équivalents.
Preuve :
- Toute clause de
Δi+1∪Θi+1 est
conséquence de
Δi∪Θi. En effet toute clause de
Δi+1∪Θi+1 est élément de
Δi∪Θi ou résolvant de deux éléments de cet ensemble, donc est
conséquence de cet ensemble.
- Toute clause de
Δi∪Θi est conséquence de
Δi+1∪Θi+1. Soit
C∈Δi∪Θi. Nous distinguons deux cas possibles :
-
C∈Θi+1, ainsi C est conséquence de
Δi+1∪Θi+1.
-
C
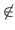 Θi+1, ainsi C contient une clause de
Δi+1 donc est conséquence de
Δi+1∪Θi+1.
Θi+1, ainsi C contient une clause de
Δi+1 donc est conséquence de
Δi+1∪Θi+1.

Preuve : Par définition Δ0 est l'ensemble obtenu par réduction de
Γ, d'après la propriété 2.1.28, ces deux
ensembles sont équivalents. Puisque Θ0 est vide, Γ
est équivalent à
Δ0∪Θ0. D'après la
propriété 2.2.5 et par récurrence,
Δ0∪Θ0 est équivalent à l'ensemble de clauses
Δk∪Θk. Puisque l'algorithme termine quand Δk est
l'ensemble vide, les ensembles Γ et Θk sont
équivalents.
Nous montrons que l'ensemble Θk est l'ensemble des clauses
minimales pour la déduction de Γ.
Propriété 2.2.7
Toute clause de Δi (où i≤k) a une preuve sans tautologie
de hauteur i à partir de Γ.
Toute clause de Θi (où i≤k) a une preuve sans tautologie
de hauteur inférieure à i à partir de Γ.
Preuve : Nous effectuons une preuve par récurrence sur i.
- Pour i = 0, c'est évident.
- Admettons cette propriété au rang i et montrons qu'elle reste
vraie au rang i + 1. Soit
C∈Δi+1, par construction
C est un résolvant entre une clause
D∈Δi et une clause
E∈Δi∪Θi et C n'est pas une tautologie. Par
hypothèse de récurrence, D a une preuve, sans tautologie, de
hauteur i , à partir de Γ, et E a une preuve, sans
tautologie, de hauteur au plus i, à partir de Γ. Donc C
a une preuve, sans tautologie, de hauteur i + 1, à partir de
Γ. Soit
C∈Θi+1, par construction
C∈Δi∪Θi, donc par hypothèse de récurrence, C a une
preuve sans tautologie à partir de Γ de hauteur au plus i.

Preuve : Nous faisons un raisonnement par récurrence.
- Pour i = 0, c'est évident car l'ensemble Δ0 est obtenu
par réduction de Γ et que
Θ0 = ∅.
- Supposons que l'ensemble
Δi∪Θi soit
réduit. Montrons qu'il en est de même de l'ensemble
Δi+1∪Θi+1. Par construction, l'ensemble
Δi+1 est
réduit. Par construction, l'ensemble
Θi+1 est un
sous-ensemble de
Δi∪Θi, donc par hypothèse de
récurrence, il est réduit. Supposons que l'ensemble
Δi+1∪Θi+1 ne soit pas réduit, il n'y a que deux
possibilités :
-
C∈Δi+1 contient une clause
D∈Θi+1 :
par construction de
Θi+1,
D∈Δi∪Θi,
ce qui implique, par construction
C
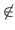 Δi+1. Nous
avons une contradiction.
Δi+1. Nous
avons une contradiction.
-
C∈Θi+1 contient une clause
D∈Δi+1 :
par construction de
Θi+1, ce cas est aussi impossible.
Par suite, l'ensemble
Δi+1∪Θi+1 est réduit.
Preuve : Nous montrons le résultat par induction sur i.
- Pour i = 0, la propriété est vraie car Θ0 est vide.
- Supposons que pour i < k, nous avons :
Θi⊂
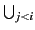 Δj. Par construction,
Θi+1 est un
sous-ensemble de
Δi∪Θi. En utilisant l'hypothèse
de récurrence, c'est donc un sous-ensemble de
Δj. Par construction,
Θi+1 est un
sous-ensemble de
Δi∪Θi. En utilisant l'hypothèse
de récurrence, c'est donc un sous-ensemble de
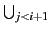 Δj.
Δj.

Propriété 2.2.10
Pour tout i≤k, un résolvant non valide de deux clauses de Θi contient une clause de
Δi∪Θi.
Preuve : Par induction sur i nous avons :
- Pour i = 0, la propriété est vraie car Θ0 est vide.
- Supposons la propriété vérifiée pour i < k. Soient
C, D∈Θi+1 ayant un résolvant E non valide. Montrons que E
contient une clause de
Δi+1∪Θi+1. D'après la
propriété 2.2.9,
C, D∈
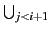 Δj. Nosu distinguons deux cas possibles :
Δj. Nosu distinguons deux cas possibles :
- Supposons
C∈Δi ou
D∈Δi. Nous avons deux
cas :
-
E∈Δi+1, donc E contient un élément de
Δi+1∪Θi+1
-
E
 Δi+1, donc, par construction, soit E
contient une autre clause de
Δi+1 donc de
Δi+1∪Θi+1, soit E contient une clause
F∈Δi∪Θi. Nous distinguons deux cas pour F :
Δi+1, donc, par construction, soit E
contient une autre clause de
Δi+1 donc de
Δi+1∪Θi+1, soit E contient une clause
F∈Δi∪Θi. Nous distinguons deux cas pour F :
-
F∈Θi+1 donc E contient
F∈Δi+1∪Θi+1.
-
F
 Θi+1 donc, par construction de cet ensemble,
F inclut une clause
G∈Δi+1. Donc E contient
G∈Δi+1∪Θi+1.
Θi+1 donc, par construction de cet ensemble,
F inclut une clause
G∈Δi+1. Donc E contient
G∈Δi+1∪Θi+1.
Ainsi dans ces deux cas, E contient une clause élément de
Δi+1∪Θi+1.
- Supposons
C
 Δi et
D
Δi et
D  Δi. Puisque
les clauses de
Θi+1 sont des clauses de
Δi∪Θi, nous avons donc
C, D∈Θi. Par hypothèse
de récurrence, E contient une clause
F∈Δi∪Θi. Comme dans le cas précédent, nous en déduisons que E
contient une clause de
Δi+1∪Θi+1.
Δi. Puisque
les clauses de
Θi+1 sont des clauses de
Δi∪Θi, nous avons donc
C, D∈Θi. Par hypothèse
de récurrence, E contient une clause
F∈Δi∪Θi. Comme dans le cas précédent, nous en déduisons que E
contient une clause de
Δi+1∪Θi+1.
Par suite, dans ces deux cas, E contient une clause de
Δi+1∪Θi+1.
Propriété 2.2.11
Si la clause C contient une clause de
Δi∪Θi alors,
pour tout j tel que
i≤j≤k,
C contient une clause de
Δj∪Θj.
Preuve : La preuve est une récurrence élémentaire sur j.
- Pour j = i, la propriété est triviale.
- Supposons que C contient une clause
D∈Δj∪Θj où
i≤j < k. Montrons que C contient une clause de
Δj+1∪Θj+1. Nous distinguons deux cas pour
D.
-
D∈Θj+1 : donc C contient une clause de
Δj+1∪Θj+1.
-
D
 Θj+1. Par construction de
Θj+1, D contient E où
E∈Δj+1.
Donc C contient une clause de
Δj+1∪Θj+1.
Θj+1. Par construction de
Θj+1, D contient E où
E∈Δj+1.
Donc C contient une clause de
Δj+1∪Θj+1.
Ainsi dans les deux cas, C contient une clause de
Δj+1∪Θj+1.

Propriété 2.2.12
Toute clause non valide déduite de Γ contient un élément de Θk.
Preuve : Supposons que toute clause non valide ayant une preuve de longueur
inférieure à n à partir de Γ contienne un élément de
Θk. Soit C une clause non valide déduite de Γ par
une preuve de longueur n. Montrons que C contient une clause de
Θk. Soit
C∈Γ, soit C est résolvant de deux
clauses D et E précédant C dans la preuve de C. Examinons
ces deux cas.
-
C∈Γ. Puisque C n'est pas valide et que Δ0
est obtenu par réduction de Γ, C contient une clause de
Δ0. Puisque Θ0 est vide, C contient une clause de
Δ0∪Θ0. D'après la
propriété 2.2.11, C contient une clause de
Δk∪Θk donc de Θk, puisque Δk est
vide.
- C est résolvant de D et E, clauses déduites de Γ
par des preuves de longueurs inférieures à n. D'après la
propriété 2.1.8, si D et E étaient
valides, il en serait de même de C, donc l'une des clauses D, E
n'est pas valide.
- Supposons E valide. Donc D n'est pas valide et, par
hypothèse de récurrence, contient
D'∈Θk. Puisque,
d'après cette même propriété 2.1.8, C
contient D, C contient un élément de Θk.
- Supposons D valide. De façon analogue, C contient un élément
de Θk.
- Supposons que ni D, ni E ne soient valides. Par hypothèse de
récurrence, D contient
D'∈Θk et E contient
E'∈Θk. Puisque C est résolvant de D et E, il existe un
littéral L tel que L∈D, Lc∈E et
C = (D - {L})∪(E - {Lc}). Examinons les deux cas exhaustifs suivants :
- Supposons
L
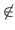 D' ou
Lc
D' ou
Lc 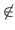 E'. Nous avons
D'⊂C ou
E'⊂C. Par suite, C contient un élément de
Θk.
E'. Nous avons
D'⊂C ou
E'⊂C. Par suite, C contient un élément de
Θk.
- Supposons L∈D' et
Lc∈E'. Soit
C' = (D' - {L})∪(E' - {Lc}). C' est un résolvant de D' et E' et
C contient C'. D'après la propriété 2.2.10,
puisque D' et E' sont éléments de Θk, C' est élément
de
Δk∪Θk, donc de Θk, puisque Δk
est vide. Donc C contient un élément de Θk.
Ainsi dans tous les cas, C contient un élément de Θk.
Propriété 2.2.13
Θk est l'ensemble des clauses minimales pour la déduction de Γ.
Preuve :
- Soit C une clause minimale pour la déduction de Γ.
Montrons que
C∈Θk. Puisque C est une clause non valide
déduite de Γ, d'après la
propriété 2.2.12, C contient une clause
D∈Θk. D'après la propriété 2.2.7, la
clause D est aussi déduite de Γ et puisque C est minimale
pour la déduction de Γ et que C contient D, nous avons C = D, donc
C∈Θk.
- Soit
C∈Θk. Montrons que C est minimale pour la
déduction de Γ. Supposons, au contraire, que C contienne
strictement une clause D déduite de Γ. D'après la
propriete 2.2.12, D contient une clause de
Θk, donc
C∈Θk contient strictement une clause de
Θk. Par suite, l'ensemble Θk ne serait pas réduit,
ce qui contredit la propriété 2.2.8. En effet
d'après cette propriété, l'ensemble
Δk∪Θk est
réduit et, puisque Δk est vide, l'ensemble Θk est
réduit.

La méthode de Davis-Putnam-Logemann-Loveland ( DPLL) fut crée en 1960 par Martin Davis et
Hillary Putnam, puis améliorée en 1962 par Martin Davis, George
Logemann et Donald Loveland. L'algorithme DPLL permet de
décider si un ensemble de clauses est satisfaisable. Bien que cet
algorithme date de plus de 50 ans, de nombreuses variantes en sont
encore étudiées, car il est bien meilleur que ceux précedemment
étudiés (table de vérité, transformation en somme de monômes ou
produit de sommes, stratégie complète). Nous remarquons d'abord qu'il
y a deux types de transformations de formules :
- Celles qui préservent le sens, c'est-à-dire transforment une
formule en une autre formule équivalente.
- Celles qui préservent seulement la satisfaisabilité,
c'est-à-dire transforment une formule satisfaisable en une autre
formule satisfaisable.
L'efficacité de l'algorithme DPLL vient de l'utilisation des
transformations préservant seulement la satisfaisabilité, car ces
transformations sont moins coûteuses que celles préservant le
sens. Nous introduisons d'abord la suppression des clauses contenant
des littéraux isolés, puis la résolution unitaire et enfin la
simplification des clauses valides. Ces transformations constituent
les briques de base de l'algorithme DPLL. L'idée principale de
cet algorithme, partant d'un ensemble de clauses «irréductibles
», est de choisir une variable et de considérer les deux situations
possibles : le cas où elle est vraie et le cas où elle est
fausse. Ainsi les deux ensembles de clauses obtenus peuvent
éventuellement se simplifier, sinon le choix d'une nouvelle variable
est nécessaire. Dans le pire des cas il s'agit de construire la
table de vérité correspondante aux clauses, mais en pratique de
nombreuses simplifications apparaissent et permettent à cet algorithme
de conclure efficacement.
2.3.1 Suppression des clauses contenant des littéraux
isolés
Comme nous ne cherchons pas à préserver l'équivalence de formule mais
la satisfiabilité, nous avons la liberté de choisir la valeur de
certaines variables. En particulier une variable qui n'apparaît que
sous la forme d'un littéral positif ou négatif sera dite
isolée. Nous pouvons alors affecter la valeur adéquate à cette
variable afin de rendre vraies toutes les occurrences du littéral
associé, ceci sans changer la satisfiabilité de l'ensemble de clauses
considéré.
Définition 2.3.1 (Littéral isolé
)
Soient Γ un ensemble de clauses et L un littéral élément
d'une clause de Γ, L est un littéral isolé
(relativement à Γ), si aucune clause de Γ ne comporte
de littéral complémentaire de L.
Lemme 2.3.2
La suppression des clauses qui comportent un littéral isolé, préserve
la satisfaisabilité.
La preuve est demandée dans l'exercice 48.
Exemple 2.3.3
Soit Γ l'ensemble de clauses
{p + q + r,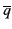 +
+ 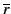 , q + s,
, q + s,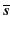 + t}.
+ t}.
2.3.2 Résolution unitaire
Définition 2.3.4
Une clause unitaire est une clause qui
ne comporte qu'un littéral.
Les clauses unitaires sont aussi des clauses particulières qui sont :
- soit isolées et donc seront traitées par la simplification
précédente,
- soit de potentiels résolvants, dans ce cas il faut effectuer la
résolution dite «unitaire » de ces clauses.
Lemme 2.3.5
Soit Γ un ensemble de clauses. Soit L l'ensemble des
littéraux des clauses unitaires de Γ. Soit Θ
l'ensemble de clauses ainsi obtenu à partir de Γ :
- Si L comporte deux littéraux complémentaires, alors
Θ = {
 }.
}.
- Sinon Θ est obtenu ainsi :
- •
- Nous enlevons les clauses qui comportent un élément de L.
- •
- À l'intérieur des clauses restantes nous enlevons
les littéraux complémentaires des éléments de L.
Γ a un modèle si et seulement si Θ en a un.
La preuve est demandée dans l'exercice 49.
Exemple 2.3.6
- Soit Γ l'ensemble de clauses :
p + q,
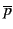 ,
,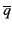 .
.
- Soit Γ l'ensemble de clauses :
a + b +
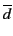 ,
,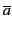 + c +
+ c + 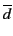 ,
,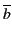 , d,
, d,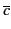 .
.
- Soit Γ l'ensemble de clauses :
p, q, p + r,
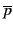 + r, q +
+ r, q + 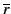 ,
,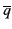 + s.
+ s.
2.3.3 Suppression des clauses valides
Enfin la dernière transformation utilisée dans l'algorithme DPLL
est de simplement enlever les clauses valides d'un ensemble de
clauses. Ceci peut paraître une évidence mais cette transformation
est une des idées centrales de cet algorithme, une fois une variable
affectée à une valeur, elle est implicitement utilisée dans la
suppression de clauses contenant des littéraux isolés.
Lemme 2.3.7
Soit Γ un ensemble de clauses. Soit Θ l'ensemble de
clauses obtenu en supprimant les clauses valides de Γ. Γ
a un modèle si et seulement si Θ en a un.
Preuve :
- Supposons que Γ a un modèle v, comme Θ est un
sous-ensemble des clauses de Γ, v est aussi modèle de
Θ. Donc, Θ a un modèle.
- Supposons que Θ a un modèle v. Soit v' une
assignation de Γ telle que
v'(x) = v(x) pour toute variable
x présente à la fois dans Γ et Θ. Soit C une
clause de Γ. Si C est aussi une clause de Θ, alors
v' est un modèle de C car v et v' donnent la même valeur à
C. Si C n'est pas une clause de Θ, alors C est valide,
en conséquence toute assignation, v' en particulier, est modèle de
C. D'où, Γ a un modèle: v'.

Nous donnons une version de l'algorithme DPLL dans la
figure 2.1 dans la fonction Algo_DPLL. Nous pouvons
constater dans l'algorithme que nous supprimons une seule fois les
clauses valides avant de réellement commencer les
simplifications. Cela se justifie par le fait que l'algorithme ne
pourra pas produire de nouvelles clauses valides. En effet, il ne fait
qu'enlever des littéraux des clauses initialement données. Par suite,
il est inutile d'enlever des clauses valides lors de l'étape de
réduction, puisqu'il n'y aura plus de telles clauses. La fonction DPLL teste d'abord si la clause vide a été générée, puis effectue
les simplifications possibles avant de choisir une variable pour
appliquer récursivement la même fonction dans le cas où cette
variable est affectée à vraie et dans le cas où elle est affectée à
faux.
Figure 2.1:
Algorithme de Davis-Putnam-Logemann-Loveland.
| bool fonction Algo_DPLL( Γ : ensemble de clauses) |
| 0 |
Supprimer les clauses valides de Γ. |
| |
Si
Γ = ∅, retourner (vrai). |
| |
Sinon retourner (DPLL(Γ)) |
| |
|
| bool fonction DPLL( Γ : ensemble de clauses non valides) |
| La fonction retourne vrai si et seulement si Γ est satisfaisable |
| 1 |
Si
 ∈Γ, retourner(faux). ∈Γ, retourner(faux). |
| |
Si
Γ = ∅, retourner (vrai). |
| 2 |
Réduire Γ : il suffit d'enlever toute clause contenant une autre clause. |
| 3 |
Enlever de Γ les clauses comportant des littéraux isolés (cf. paragraphe 2.3.1). |
| |
Si l'ensemble Γ a été modifié, aller en 1. |
| 4 |
Appliquer à Γ la résolution unitaire (cf paragraphe 2.3.2). |
| |
Si l'ensemble Γ a été modifié, aller en 1. |
| 5 |
Choisir x une variable quelconque de Γ |
| |
retourner (DPLL(
Γ[x : = 0]) ou alors DPLL(
Γ[x : = 1])) |
|
Pour obtenir une trace de l'algorithme, nous supprimons les clauses
valides, en abrégé VAL, puis nous dessinons l'arbre des appels avec
l'argument de la fonction ainsi que les ensembles obtenus par les
étapes 2 (réduction, en abrégé RE), 3 (enlèvement des clauses ayant
des littéraux isolés, en abrégé ELI) et 4 (résolution unitaire, abrégé
en RU). À cause du «ou alors», il est inutile de poursuivre la
construction de cet arbre dès que la réponse vrai (attachée à un
ensemble vide) a été obtenue.
Exemple 2.3.8
Nous illustrons l'application de cet algorithme sur deux ensembles de
clauses.
Preuve : La réduction et les transformations 2.3.1, 2.3.2 et
2.3.3 préservent l'existence d'un modèle, donc au
pas 0 et 1, l'algorithme vérifie l'invariant suivant : la valeur
courante de l'ensemble de clauses de Γ a un modèle si et
seulement si Γ a un modèle. Nous en déduisons immédiatement
que les réponses de l'algorithme, fournies au pas 0 ou 1, sont
correctes. Au pas 5, pour les mêmes raisons, la valeur courante de
l'ensemble de clauses de Γ, lors de l'appel de DPLL, a
un modèle si et seulement si Γ a un modèle. Supposons les
appels récursifs corrects :
- Si DPLL(
Γ[x : = 0]) est vrai, par récurrence
Γ[x : = 0] est satisfaisable donc Γ est satisfaisable
(nous utilisons le résultat 2.1.21 : Γ est
satisfaisable ssi
Γ[x : = 0] est satisfaisable ou
Γ[x : = 1]
est satisfaisable), ce qui correspond à la valeur vrai de
DPLL(Γ).
- Si DPLL(
Γ[x : = 0]) est faux, par récurrence
Γ[x : = 0] est insatisfaisable. Dans ce cas, DPLL(Γ) vaut
DPLL(
Γ[x : = 1]) :
- Supposons que DPLL(
Γ[x : = 1]) soit vrai alors par récurrence
Γ[x : = 1] est satisfaisable donc Γ est satisfaisable, ce
qui correspond à la valeur vrai de DPLL(Γ).
- Supposons que DPLL(
Γ[x : = 1]) soit faux, alors par récurrence
Γ[x : = 1] est insatisfaisable. Donc Γ est
insatisfaisable, ce qui correspond à la valeur faux de DPLL(Γ).

Preuve : Au pas 0, la fonction Algo_DPLL consiste en un test, puis soit le
renvoi de la valeur vrai soit l'appel de la fonction DPLL(Γ). Le pas 0 consiste en la suppression de clauses de
l'ensemble de départ, cet ensemble étant fini, le pas 0
termine. Donc, la fonction Algo_DPLL termine si la fonction DPLL(Γ) termine.
Considérons un appel de la fonction DPLL(Γ). Le pas 1
est constitué d'un test et d'instructions élémentaires, donc il
termine. Le pas 2 consiste à réduire Γ qui est un ensemble
fini. La réduction consistant à supprimer des clauses, elle
termine. Le pas 3 consiste à supprimer des clauses, puis
éventuellement retourner au pas 1. Le nombre de clauses étant fini,
soit l'algorithme termine en 1, soit le pas 4 débute. De la même
manière, le pas 4 consiste à supprimer des clauses et des variables,
qui sont en nombres finis, puis éventuellement retourner au pas
1. Le nombre de clauses et de variables étant fini, soit
l'algorithme termine en 1, soit le pas 5 débute. Le pas 5 consiste
en un ou deux appels récursifs sur un ensemble de clauses où une
variable a disparu (la valeur d'une variable est fixée). Ainsi, la
récurrence en 5 se termine car à chaque appel récursif le nombre de
variables diminue strictement. D'où, l'algorithme Algo_DPLL
termine.
Remarque 2.3.11 (Oubli de simplifications)
L'algorithme Algo_DPLL a été donné avec les étapes de «
simplification» : suppression des clauses valides (0), réduction
(2), enlèvement des littéraux isolés (3) et réduction unitaire
(4). L'algorithme reste correct si nous omettons ces étapes, ou si
nous ne faisons qu'une partie des simplifications, ce qui est
souvent le cas lorsque nous faisons une trace de l'exécution sans
machine. Car sans machine il est fréquent d'oublier des
simplifications, ce qui ne nuit pas car l'algorithme reste correct.
Remarque 2.3.12 (Choix de la variable)
Un bon choix pour la variable x de l'étape (5), consiste à choisir
la variable qui apparaît le plus souvent. Un meilleur choix
consiste à choisir la variable qui va entraîner par la suite le plus
de simplifications : il faut faire des compromis entre le temps
passé à choisir la «bonne» variable et l'importance des
simplifications induites par ce choix. Plusieurs heuristiques
classique de choix de variable sont présenté dans le
paragraphe 2.3.5.1.
2.3.5 Solveurs SAT
Le problème SAT est un problème
de décision qui consiste à déterminer si une formule propositionnelle
en forme normale conjonctive admet ou non un modèle. Ce problème est
le problème NP-complet de
référence [5]. Généralement, seule une version de ce
problème, appelée 3-SAT, où toutes les clauses de la formule sont constituées
d'exactement trois littéraux, est considérée, car des réductions
linéaires existent
pour passer de SAT à 3-SAT. Un exemple de réduction SAT vers
3-SAT est étudié dans l'exercice 50.
Des programmes performants sont dédiés à la résolution du problème SAT
2.1. Ces programmes sont
appelés des solveurs SAT et sont généralement
classés en deux catégories :
- Les solveurs SAT «complets »
sont généralement des versions améliorées de l'algorithme DPLL. Parmi les solveurs SAT complets les plus utilisés à l'heure
actuelle, nous pouvons citer par exemple zchaff, satz,
march ou encore GRASP.
- Les solveurs SAT «incomplets »
sont des algorithmes de semi-décision qui finissent par trouver un
modèle à la formule, s'il existe et qui ne termine pas dans le cas
contraire. Ces algorithmes sont fondés sur des marches aléatoires
dans l'espace d'état. Dans cette catégorie, nous pouvons citer les
algorithmes par exemple WalkSAT et GSAT.
Nous décrivons maintenant, de manière non-exhaustive, les principales
améliorations de l'algorithme DPLL utilisées dans les solveurs
SAT complets.
2.3.5.1 Heuristique de branchement
Le choix de la prochaine variable à affecter a un impact important sur
la taille de l'arbre de recherche développé par DPLL. Ainsi, le
choix de l'heuristique de branchement est déterminant dans les
algorithmes fondés sur DPLL. Les heuristiques de branchement
sont souvent basées sur des arguments syntaxiques tels que la taille
des clauses, le nombre d'occurences, etc. Parmi les
heuristiques les plus connues, nous pouvons citer :
- MOMS :
- L'heuristique MOMS (pour Maximum Occurences in Clauses
of Minimum Size) consiste, comme son nom l'indique, à sélectionner
la variable ayant le plus d'occurences dans les clauses les plus
courtes. Les choix effectués par cette heuristique favorisent la
propagation unitaire.
- JW :
- L'heuristique JW (pour Jeroslow-Wang) utilise également la
longueur des clauses. En effet, un poids est affecté à chaque
littéral en fonction de la taille des clauses où il apparaît. La
possibilité qu'une variable soit sélectionnée par JW est inversement
proportionnelle à la somme des tailles des clauses où elle apparaît.
- UP :
- Contrairement aux deux heuristiques précédentes,
l'heuristique UP (pour Unit Propagation) n'est pas fondée sur des
arguments syntaxiques. Cette heuristique essaie de sélectionner une
variable en prévoyant à l'avance son effet sur la recherche. Elle
consiste à calculer un poids pour chaque variable en fonction des
simplifications qu'elle génère par propagation unitaire.
L'idée est d'ajouter des clauses, en pré-traitement, à l'ensemble initial de
clauses . Le nouvel ensemble de clauses reste équivalent à
l'ensemble initial. Par exemple, nous pouvons citer la résolution
restreinte qui
consiste à ajouter des résolvants de taille bornée. Ce type de méthode
permet de réduire la taille de l'arbre recherche en amenant aux
contradictions plus tôt dans la recherche.
Lorsque l'algorithme DPLL atteint une contradiction (un
conflit), il revient (chronologiquement) au dernier
branchement de variable effectué. Or, ce branchement n'est pas
nécessairement l'une des décisions à l'origine de la
contradiction. L'analyse des conflits remédie à ce problème en tenant
compte des décisions à l'origine du conflit. Cette analyse permet
ainsi d'effectuer un retour-arrière non-chronologique, c'est-à-dire un
retour direct au niveau, plus haut dans l'arbre, qui est à l'origine
du conflit sans tester les niveaux intermédiaires.
L'apprentissage consiste à analyser et apprendre les raisons qui ont
amené à une contradiction : lorsqu'une assignation partielle amène à
une contraction, il est possible d'isoler un sous-ensemble
d'assignations et un sous-ensemble de clauses, qui sont responsables
du conflit. À partir de ces assignations, il est possible de
construire (d'apprendre) une clause qui est impliquée par ces
clauses. Cette nouvelle clause est ajoutée à l'ensemble de clauses du
problème. Les assignations pertinentes sont déterminées par un graphe
de dépendance entre les clauses et les assignations, appelé graphe d'implication. Les clauses
apprises permettent de ne pas refaire plusieurs fois les mêmes «erreurs » dans l'arbre de recherche.
La plupart des solveurs SAT actuels utilisent une stratégie de
redémarrage, qui consiste à redémarrer la recherche en prenant en
compte de nouvelles clauses apprises durant la recherche
précédente. La plupart des solveurs effectuent un redémarrage après
qu'un seuil de clauses apprises soit atteint. Ainsi, à chaque
redémarrage, le parcours de l'espace de recherche change car
l'ensemble de clauses est modifié. Il faut noter que la plupart des
solveurs effacent régulièrement les clauses apprises. Ainsi, le mixage
des redémarrages et des oublis peut dans certains cas mettre en cause
la complétude des solveurs. Un paramétrage des redémarrages est donc
nécessaire pour garder cette dernière propriété. Le solveur Chaff, par
exemple, augmente à chaque redémarrage le seuil au-delà duquel une
clause est oubliée. Ainsi, de plus en plus de clauses sont gardées, ce
qui assure la complétude.
Dans les solveurs SAT modernes, 80% du temps de calcul est consommé
par la propagation unitaire. Ainsi, des structures de données dites
«paresseuses » ont été introduites
dans le but d'optimiser la propagation unitaire.




suivant: 3. Déduction Naturelle
monter: I. Logique propositionnelle
précédent: 1. Logique propositionnelle
Table des matières
Index
Benjamin Wack
2013-01-08
![]() + c, c'est-à-dire
a + b,
+ c, c'est-à-dire
a + b, ![]() + c
+ c ![]() a + c. En
utilisant la propriété 1.2.27, il suffit de démontrer que la
formule
(a + b).(
a + c. En
utilisant la propriété 1.2.27, il suffit de démontrer que la
formule
(a + b).(![]() + c)⇒(a + c) est valide. Pour
cela, nous pouvons utiliser une table de vérité (8 lignes) ou alors
une simplification de formules comme dans
l'exercice 13. Ces deux méthodes sont
fastidieuses même pour des formules aussi simples (3 variables
uniquement). En utilisant la règle de résolution présentée dans ce
chapitre, nous déduisons directement la clause a + c à partir des deux
clauses a + b et
+ c)⇒(a + c) est valide. Pour
cela, nous pouvons utiliser une table de vérité (8 lignes) ou alors
une simplification de formules comme dans
l'exercice 13. Ces deux méthodes sont
fastidieuses même pour des formules aussi simples (3 variables
uniquement). En utilisant la règle de résolution présentée dans ce
chapitre, nous déduisons directement la clause a + c à partir des deux
clauses a + b et
![]() + c.
+ c.
![]() est conséquence de Γ,
autrement dit si Γ est insatisfaisable, alors
est conséquence de Γ,
autrement dit si Γ est insatisfaisable, alors ![]() peut être
retrouvé par résolution à partir de Γ.
peut être
retrouvé par résolution à partir de Γ.
![[*]](crossref.png) ). Comme nous le verrons dans la
suite deux clauses qui ont le même ensemble de littéraux jouent le
même rôle dans la résolution. Aussi, nous définissons deux clauses
égales comme étant deux clauses avec le même ensemble de littéraux.
). Comme nous le verrons dans la
suite deux clauses qui ont le même ensemble de littéraux jouent le
même rôle dans la résolution. Aussi, nous définissons deux clauses
égales comme étant deux clauses avec le même ensemble de littéraux.
![]() est la clause vide et
s(
est la clause vide et
s(![]() ) = ∅.
) = ∅.
![]() est équivalent à L mais n'est pas
un littéral : un littéral est une variable ou la négation
d'une variable mais la double négation d'une variable n'est pas un
littéral.
est équivalent à L mais n'est pas
un littéral : un littéral est une variable ou la négation
d'une variable mais la double négation d'une variable n'est pas un
littéral.
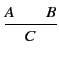
![]()
![]() + p n'est pas une clause, bien que
les deux opérandes de la disjonction soient des clauses.
Aussi nous introduisons un nouvel opérande,
+ p n'est pas une clause, bien que
les deux opérandes de la disjonction soient des clauses.
Aussi nous introduisons un nouvel opérande, ![]() , afin de
combiner la disjonction et l'élimination de
, afin de
combiner la disjonction et l'élimination de ![]() . Cet opérande va
nous permettre de simplifier la définition de résolvant.
. Cet opérande va
nous permettre de simplifier la définition de résolvant.
![]() L. Munis de cette définition, nous pouvons reformuler plus
simplement la règle de résolution.
L. Munis de cette définition, nous pouvons reformuler plus
simplement la règle de résolution.
![]() C. Par définition, il existe une
preuve P de C à partir de Γ. Supposons que pour toute
preuve de D à partir de Γ, plus courte que P, nous
avons
Γ
C. Par définition, il existe une
preuve P de C à partir de Γ. Supposons que pour toute
preuve de D à partir de Γ, plus courte que P, nous
avons
Γ ![]() D. Montrons que
Γ
D. Montrons que
Γ ![]() C. Nous
avons deux cas possibles :
C. Nous
avons deux cas possibles :
![]() Lc à partir de Γ en
ajoutant le littéral Lc aux clauses où nous l'avions
enlevé. Formalisons cette ébauche de preuve. Supposons que
Γ[L : = 1]
Lc à partir de Γ en
ajoutant le littéral Lc aux clauses où nous l'avions
enlevé. Formalisons cette ébauche de preuve. Supposons que
Γ[L : = 1] ![]() C. Il y a une preuve P de C à partir de
Γ[L : = 1]. Supposons que pour toute preuve de D à partir de
Γ[L : = 1], plus courte que P, nous avons
Γ
C. Il y a une preuve P de C à partir de
Γ[L : = 1]. Supposons que pour toute preuve de D à partir de
Γ[L : = 1], plus courte que P, nous avons
Γ ![]() D ou
Γ
D ou
Γ ![]() D
D![]() Lc. Nous avons deux cas possibles :
Lc. Nous avons deux cas possibles :
![]() C. Puisque
Γ[L : = 0] = Γ[Lc : = 1] et que Lcc = L, d'après le lemme
2.1.22 nous avons
Γ
C. Puisque
Γ[L : = 0] = Γ[Lc : = 1] et que Lcc = L, d'après le lemme
2.1.22 nous avons
Γ ![]() C ou
Γ
C ou
Γ ![]() C
C![]() L.
L.![]()
![]()
![]() par
récurrence sur n. Supposons que pour tout ensemble Δ de
clauses insatisfaisable avec moins de n variables, nous avons
Δ
par
récurrence sur n. Supposons que pour tout ensemble Δ de
clauses insatisfaisable avec moins de n variables, nous avons
Δ ![]()
![]() .
.
![]()
![]() .
.
![]() Δj. D'après la propriété précédente, C
inclut une clause de
Δi∪Θi. Donc par
construction de
Δi+1,
C
Δj. D'après la propriété précédente, C
inclut une clause de
Δi∪Θi. Donc par
construction de
Δi+1,
C ![]() Δi+1,
contradiction. Par suite,
C
Δi+1,
contradiction. Par suite,
C ![]()
![]() Δj.
Δj.
![]()
![]() +
+ ![]() ,
,![]() + s, p + q,
+ s, p + q,![]() +
+ ![]() . Nous donnons la trace de l'algorithme.
. Nous donnons la trace de l'algorithme.
![]()