



suivant: II. Logique du premier
monter: I. Logique propositionnelle
précédent: 2. Résolution propositionnelle
Table des matières
Index
Sous-sections
3. Déduction Naturelle
Une preuve dans les cours de Mathématiques est une
décomposition du raisonnement en pas élémentaires évidents, nous
pratiquons alors sans le savoir la déduction naturelle. Dans ce
chapître, nous présentons un système formel qui est une modélisation
particulière de la déduction naturelle. La déduction naturelle et le
calcul de séquent furent introduits en 1934 par
Gerhard Gentzen (1909-1945)
[12,13]. Les preuves dans notre système ne sont pas
des arbres comme dans le système original de Gehard Gentzen mais
ressemblent plus aux preuves des mathématiciens. Nous expliquons aussi
comment faire le lien entre ces deux formalismes en construisant des
arbres proches de ceux introduits originellement. Nous choisissons de
ne parler que de la logique classique, par opposition à la logique intuitionniste qui est obtenue en omettant la règle
de réduction à l'absurde (la dernière règle de la
table 3.1).
Pour simplifier l'étude de la déduction naturelle, nous considérons que
le vrai, la négation et l'équivalence sont des abréviations ainsi
définies :
 abrège
abrège
 ⇒
⇒ .
.
- ¬A abrège
A⇒
 .
.
-
A⇔B abrège
(A⇒B)∧(B⇒A).
Deux formules seront considérées comme égales, si les formules
obtenues en éliminant les abréviations sont identiques. Par exemple,
les formules
¬¬a,
¬a⇒ et
(a⇒
et
(a⇒ )⇒
)⇒ sont égales. Il est clair que
deux formules égales, au sens ci-dessus, sont équivalentes (voir
exercice 54) et nous utilisons implicitement cette
propriété quand nous remplaçons une formule par une autre formule
égale aux abréviations près.
sont égales. Il est clair que
deux formules égales, au sens ci-dessus, sont équivalentes (voir
exercice 54) et nous utilisons implicitement cette
propriété quand nous remplaçons une formule par une autre formule
égale aux abréviations près.
Nous décrivons tout d'abord notre système de
règles de déduction naturelle et introduisons la notion de preuve dans
ce contexte. Ensuite, nous présentons des tactiques pour aider le
lecteur à la rédaction de preuve. Nous montrons la cohérence et la
complétude de notre système. Enfin nous présentons un outil permettant
à partir d'une formule de construire automatiquement une preuve ou
bien d'exhiber un contre-exemple.
Nous présentons d'abord les règles du système de la déduction
naturelle. Elles constituent les raisonnements élémentaires autorisés.
Ensuite nous exposons la notion de preuve qui se
construit par applications successives de ces règles.
Définition 3.1.1 (Règle
)
Une règle est constituée de formules dites hypothèses
H1,…, Hn et d'une conclusion. Les hypothèses sont écrites
au-dessus d'un trait et l'unique formule en dessous de ce trait est
la conclusion de la règle. Le nom d'une règle est écrit au même
niveau que le trait séparant hypothèses et conclusion.
La déduction naturelle que nous présentons comporte une dizaine de
règles de déduction qui sont regroupées dans la
table 3.1. La règle fondamentale est la suivante : si
nous pouvons déduire une formule B d'une hypothèse A, alors nous
pouvons déduire
A⇒B en nous passant de cette hypothèse.
Nous décrivons chacune des dix règles du système de déduction que nous
considérons. L'application de ces règles et seulement de ces règles va
nous permettre de prouver la correction des raisonnements. Il est donc
important de bien comprendre le fonctionnement de chacune d'entre
elles. Nous avons deux familles de règles pour chaque connecteur : les
règles d'introduction et les règles d'élimination. L'intuition du
rôle des règles d'introduction est de générer un symbole de la
logique afin de bâtir progressivement la formule à prouver. Les
règles d'élimination servent à simplifier un raisonnement ou à obtenir
une nouvelle formule grâce aux raisonnements déjà réalisés et ainsi
faire disparaître un connecteur logique. En plus nous avons deux
règles spéciales, que nous décrirons en dernier, une pour éliminer
deux occurrences successives de la négation et une autre pour déduire
d'importe quoi à partir du faux.
La règle d'introduction de la conjonction, notée ∧I, signifie
simplement que si nous avons une preuve de A et une preuve de B,
alors nous pouvons déduire une preuve de la proposition
A∧B. Nous pouvons aussi dire que la preuve de la proposition
A∧B peut se décomposer en une preuve de A et une preuve de B.
Les règles d'élimination de la conjonction, notées ∧E1 et
∧E2, permettent de déduire à partir de la conjonction de deux
formules
A∧B soit la formule A soit la formule B. Ainsi
nous avons éliminé le connecteur de la conjonction.
Les règles d'introduction de la disjonction sont les duales des règles
de l'élimination de la conjonction. Les deux règles d'introduction, notées
∨I1 et ∨I2, permettent de créer une conjonction de deux
clauses à partir d'une des deux clauses. Ces règles signifient
simplement que si A est vraie alors A∨B et B∨A sont
aussi vraies quelle que soit la proposition B.
La règle d'élimination de la disjonction, notée ∧E, est plus
complexe. Afin de déduire la clause C à partir de la conjonction A∨B il faut aussi prouver les prémisses suivantes : A implique
C et B implique C. Cette règle formalise la notion de preuve par cas utilisée en mathématiques : supposons que dans un
environnement donné, nous souhaitons prouver C alors que deux cas,
A ou B, sont possibles; nous nous plaçons alors dans le cas où A
est vérifié et nous prouvons C, puis nous nous plaçons dans le cas
où B est vérifié et nous prouvons C.
La règle de l'élimination de l'implication
⇒E dit que si
nous sommes capables d'obtenir une preuve de A et une preuve de
A⇒B alors nous avons une preuve de B. Cet règle
correspond au modus ponens.
La règle fondamentale de notre système est la règle d' introduction de l'implication
⇒I : si nous pouvons
déduire une formule B d'une hypothèse A, alors nous pouvons
déduire
A⇒B en nous passant de cette hypothèse.
Cette règle est résumée par le schéma ci-dessous, où la notation [A]
indique que si A est une hypothèse de la preuve de B, cette hypothèse est
enlevée de la preuve de
A⇒B, autrement dit ne sert plus
pour prouver
A⇒B.
Enfin nous avons deux règles spéciales:
- La première permet de déduire
n'importe quoi à partir du faux : il s'agit de la «règle du faux»,
notée Efq, pour la formule latine «ex falso, quodlibet», indiquant que du faux, on
peut déduire ce qu'on veut.
- La seconde est la règle de réduction à l'absurde, notée
RAA. Elle élimine deux occurrences successives de la négation.
Nous regroupons l'ensemble des règles de la déduction naturelle
dans la table 3.1.
Tableau 3.1:
Ensemble de règles de déduction naturelle.
| Introduction |
Élimination |
| |
|
| |
|
| |
|
| |
|
| |
|
| Règle du faux |
| |
| Règle de réduction à l'absurde |
| |
|
Intuitivement une preuve est l'application successive de règles de la
déduction naturelle. Dans le système originel introduit par
Gerhard Gentzen, une preuve
est représentée par un arbre de formules (certaines formules pouvant
être marquées comme enlevées). Nous avons choisi de représenter une
preuve par une succession d'étapes de raisonnement basées sur les
règles de la déduction naturelle, ceci afin d'être plus proche des
preuves faites en mathématiques. Dans le chapitre précédent, une
preuve par résolution était constituée d'une liste de clauses. En
déduction naturelle, au cours d'une preuve, nous pouvons ajouter des
hypothèses et les enlever, ce qui rend plus complexe la définition de
ce qu'est une preuve. Nous introduisons donc plusieurs notions
intermédiaires afin de définir clairement la notion de preuve en
déduction naturelle. Tout d'abord nous introduisons les composants
d'une preuve, c'est-à-dire, les «lignes d'une preuve », puis la
notion de brouillon de preuve, ensuite les contextes de ces lignes de
preuve afin de définir une preuve en déduction naturelle.
3.1.5.1 Brouillon de preuve
Une preuve est constituée d'une succession de lignes qui sont soit une
formule soit une formule précédée par le mot clef «Supposons
» ou «Donc ».
Définition 3.1.2 (
Ligne de preuve)
Une ligne de preuve est de l'une des trois formes suivantes :
- Supposons formule,
- formule,
- Donc formule.
Un brouillon de preuve est une preuve en construction, intuitivement
elle a au moins autant de Supposons que de Donc.
Définition 3.1.3 (
Brouillon de
preuve)
Un brouillon de preuve est une suite de lignes telle que, dans
tout préfixe de la suite, le nombre de lignes commençant par le mot
Supposons est au moins égal à celui des lignes commençant par
le mot Donc.
Exemple 3.1.4
Dans l'exemple ci-dessous, la suite des lignes de 1 à 3 est un
brouillon de preuve. Par contre la suite des lignes de 1 à 5,
n'est pas un brouillon de preuve car dans la suite des lignes
1 à 4, le nombre de lignes commençant par le mot Donc
dépasse celui des lignes commençant par le mot Supposons.
|
numéro |
ligne |
|
1 |
Supposons a |
|
2 |
a∨b |
|
3 |
Donc
a⇒a∨b |
|
4 |
Donc ¬a |
|
5 |
Supposons b |
Afin de pouvoir appliquer la règle d'introduction de l'implication
nous avons besoin de connaître à chaque étape d'une preuve les
formules qui sont des hypothèses utilisables. Pour ce faire, nous
associons à chaque ligne d'un brouillon de preuve un
contexte, qui est la suite des hypothèses introduites par les
lignes Supposons et non enlevées par les lignes
Donc. Puisque dans tout préfixe d'un brouillon de preuve, le
nombre de lignes commençant par le mot Supposons est au moins
égal à celui des lignes commençant par le mot Donc, le
contexte de la ligne précédant une ligne Donc n'est pas vide
et par suite le contexte de chaque ligne d'un brouillon de preuve est
bien défini. Dans la suite, nous représentons les contextes de chaque
ligne en remplaçant chaque hypothèse du contexte par le numéro de la
ligne où cette hypothèse est introduite.
Définition 3.1.5 (
Contexte)
Nous numérotons les lignes d'un brouillon de preuve de 1 à n. Pour
i de 1 à n, la liste de formules Γi est le contexte
de la ligne i. La liste Γ0 est vide et les listes de
formules Γi sont ainsi définies :
- Si la ligne i est «Supposons A», alors
Γi = Γi-1, i.
- Si la ligne i est «A» alors
Γi = Γi-1
- Si la ligne i est «Donc A» alors Γi est
obtenue en enlevant la dernière formule de
Γi-1
La liste Γi est le contexte de la ligne i.
Nous présentons nos preuves sous forme de tableaux, ce qui nous permet
de numéroter les lignes d'une preuve, les contextes utilisables, et
les règles utilisées pour générer une nouvelle ligne.
Exemple 3.1.6
Nous illustrons ici la gestion des contextes sur un brouillon de
preuve simple.
|
contexte |
numéro |
ligne |
règle |
|
1 |
1 |
Supposons a |
|
|
1,2 |
2 |
Supposons b |
|
|
1,2 |
3 |
a∧b |
∧I 1,2 |
|
1 |
4 |
Donc
b⇒a∧b |
⇒I 2,3 |
|
1,5 |
5 |
Supposons e |
|
Nous précisons la notion de conclusion et de formule utilisable afin
de définir et manipuler des preuves en déduction naturelle.
Définition 3.1.7 (
Conclusion,
formule utilisable)
Nous définissons la notion de conclusion et de formule utilisable:
- La formule figurant sur une ligne d'un brouillon de preuve est
la conclusion de la ligne.
- La conclusion d'une ligne est utilisable tant que
son contexte (c'est-à-dire les hypothèses qui ont permis de la
déduire) est présent.
Autrement dit la conclusion de la ligne i est utilisable sur la
ligne i et sur toutes les lignes suivantes dont le contexte a pour
préfixe le contexte de la ligne i.
Exemple 3.1.8
Dans l'exemple ci-dessous, la conclusion de la ligne 2 est
utilisable sur la ligne 2, et pas au delà, car à la ligne 3,
l'hypothèse qui a permis de la déduire est enlevée.
|
contexte |
numéro |
ligne |
règle |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
Nous donnons la définition de preuve dans un environnement. Un
environnement est un ensemble de formules supposées
«vraies ». Intuitivement, réaliser une preuve dans un environnement
consiste à pouvoir utiliser sans les prouver les formules de
l'environnement.
Définition 3.1.9 (
Preuve)
Soit Γ un ensemble de formules, une preuve dans
l'environnement Γ est un brouillon de preuve ayant les
propriétés suivantes :
- Pour toute ligne «Donc A», la formule A est égale
à
B⇒C, où B est la
dernière formule du contexte de la ligne précédente et où C est
une formule utilisable sur la ligne précédente ou égale
à un élément de l'environnement Γ.
- Pour toute ligne «A», la formule A est la conclusion
d'une règle (autre que la règle d'introduction de l'implication)
dont les prémisses sont utilisables sur la ligne précédente ou sont
éléments de l'environnement Γ.
La ligne «Donc A» est une application de la règle
d'introduction de l'implication. En effet, C est déduite de Γ
ou d'hypothèses qui figurent dans la ligne précédente. La liste des
hypothèses de la ligne précédente se terminant par B, nous pouvons
en déduire
B⇒C, en nous passant de l'hypothèse B.
Définition 3.1.10 (
Preuve d'une formule)
Une preuve de la formule A dans l'environnement Γ est soit la
preuve vide lorsque A est élément de
Γ, soit une preuve dont la dernière ligne est de conclusion A et de contexte vide.
Nous notons
Γ  A le fait qu'il y a une preuve de A dans
l'environnement Γ et
Γ
A le fait qu'il y a une preuve de A dans
l'environnement Γ et
Γ  P : A le fait que P est
une preuve de A dans l'environnement Γ. Lorsque
l'environnement est vide, nous l'omettons, autrement dit nous
abrégeons
∅
P : A le fait que P est
une preuve de A dans l'environnement Γ. Lorsque
l'environnement est vide, nous l'omettons, autrement dit nous
abrégeons
∅  A en
A en  A. Lorsque nous demandons
une preuve d'une formule sans indiquer d'environnement, nous supposons
que l'environnement est vide.
A. Lorsque nous demandons
une preuve d'une formule sans indiquer d'environnement, nous supposons
que l'environnement est vide.
Exemple 3.1.11
Prouvons
(a⇒b)⇒(¬b⇒¬a).
|
contexte |
numéro |
preuve |
règle |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
La preuve elle-même est ce qui figure dans la colonne preuve. Nous y
avons ajouté la numérotation des lignes de preuves, les justifications
qui indiquent les règles utilisées et les contextes de chaque ligne de
la preuve.
Nous présentons la même preuve sous forme d'arbre, ce qui correspond
à l'approche originelle de Gerhard Gentzen.
Nous remarquons que pour lever une hypothèse il est d'usage de barrer
cette hypothèse.
Exemple 3.1.12
Nous donnons la preuve de
¬A∨B dans l'environnement
A⇒B. Nous suggérons de numéroter par i, ii, iii,
etc... les formules de l'environnement pour distinguer ces numéros et
les numéros des lignes de la preuve.
|
environnement |
|
référence |
formule |
|
i |
A⇒B |
|
contexte |
numéro |
preuve |
règle |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
Nous présentons aussi la preuve précédente sous forme d'arbre.
Comme il a été rappelé dans les remarques préliminaires, nous
considérons comme égales deux formules qui sont identiques quand nous
éliminons leurs abréviations. Ainsi dans l'exemple précédent, nous
avons identifié
A⇒ et ¬A ainsi que
(¬A∨B)⇒
et ¬A ainsi que
(¬A∨B)⇒ et
¬(¬A∨B).
et
¬(¬A∨B).
3.2 Tactiques de preuve
Nous donnons des conseils pour construire des preuves. Ces conseils
sont la base du logiciel présenté dans le
paragraphe 3.5. Pour prouver la formule A dans un
environnement Γ, nous appliquons dans l'ordre les règles
suivantes, où l'ordre a été choisi de façon à reculer le plus possible
l'usage de la règle RAA :
- Si
A∈Γ, alors la preuve obtenue est vide.
- Si A est la conséquence d'une règle dont les premisses sont
dans Γ, alors la preuve obtenue est «A».
- Si Γ comporte une contradiction, c'est-à-dire une formule
B et une formule ¬B, alors la preuve obtenue est «
 ,
A».
,
A».
- Si
A = B∧C, alors :
- prouver B : Soit P la preuve obtenue pour B,
- prouver C : Soit Q la preuve obtenue pour C.
La preuve obtenue pour A est «P, Q, A».
Les preuves peuvent échouer (si l'on demande de prouver une formule
improuvable dans l'environnement donné) : Si la preuve de B ou C
échoue, il en est de même de la preuve de A. Pour simplifier la
suite, nous ne signalons plus les cas d'échecs, sauf s'ils doivent
être suivis d'une autre preuve.
- Si
A = B⇒C, alors prouver C sous l'hypothèse B
(qui est ajoutée à l'environnement). Soit P, la preuve obtenue
pour C, la preuve obtenue pour A est «Supposons
B, P, Donc A».
- Si
A = B∨C, alors prouver B : Si P est la preuve
obtenue pour B, alors «P, A» est la preuve obtenue pour
A. Si la preuve de B échoue, alors prouver C : Si P est la
preuve obtenue pour C, alors «P, A» est la preuve obtenue
pour A. Si la preuve de C échoue, essayer les règles
suivantes.
- Si
B∧C est dans l'environnement, alors prouver A à
partir des formules B, C, qui remplacent
B∧C dans
l'environnement et soit P le résultat de cette preuve. Alors «
B, C, P» est une preuve de A dans l'environnement
initial.
- Si B∨C est dans l'environnement, alors :
- prouver A dans l'environnement où B remplace B∨C :
Soit P la preuve obtenue,
- prouver A dans l'environnement où C remplace B∨C :
Soit Q la preuve obtenue.
La preuve de A est alors «Supposons B, P, Donc
B⇒A, Supposons C, Q, Donc
C⇒A, A».
- Si
¬(B∨C) est dans l'environnement, alors nous
déduisons ¬B par la preuve P4 et ¬C par la preuve P5
(preuves demandées à l'exercice 56). Soit P la preuve de
A dans l'environnement où ¬B, ¬C remplacent la formule
¬(B∨C). La preuve de A est «P4, P5, P».
- Si
A = B∨C, alors prouver C sous l'hypothèse ¬B :
soit P la preuve obtenue. «Supposons ¬B, P, Donc
¬B⇒C» est une preuve de la formule
¬B⇒C qui est équivalente à A. Pour obtenir la
preuve de A, il suffit d'ajouter la preuve P1, demandé à
l'exercice 56 de A dans l'environnement
¬B⇒C. La preuve obtenue de A est donc «Supposons ¬B, P, Donc
¬B⇒C, P1».
- Si
¬(B∧C) est dans l'environnement, alors nous en
déduisons
¬B∨¬C par la preuve P3 demandée à
l'exercice 56 puis nous raisonnons par cas comme ci-dessus :
- prouver A dans l'environnement où ¬B remplace
¬(B∧C) : Soit P la preuve obtenue,
- prouver A dans l'environnement où ¬C remplace
¬(B∧C) : Soit Q la preuve obtenue.
La preuve de A est «P3, Supposons ¬B, P, Donc
¬B⇒A, Supposons ¬C, Q, Donc
¬C⇒A, A».
- Si
¬(B⇒C) est dans l'environnement, alors nous
déduisons B par la preuve P6, ¬C par la preuve P7
(preuves demandées à l'exercice 56). Soit P la preuve de
A dans l'environnement où B, ¬C remplacent la formule
¬(B⇒C). La preuve de A est «
P6, P7, P».
- Si
B⇒C est dans l'environnement et si
C
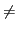
 , autrement dit si
B⇒C n'est pas égale à
¬B, alors, nous déduisons
¬B∨C dans l'environnement
B⇒C par la preuve P2 demandée à l'exercice 56
puis nous raisonnons par cas :
, autrement dit si
B⇒C n'est pas égale à
¬B, alors, nous déduisons
¬B∨C dans l'environnement
B⇒C par la preuve P2 demandée à l'exercice 56
puis nous raisonnons par cas :
- prouver A dans l'environnement où ¬B remplace
B⇒C : Soit P la preuve obtenue,
- prouver A dans l'environnement où C remplace
B⇒C : Soit Q la preuve obtenue.
La preuve de A est «P2, Supposons ¬B, P, Donc
¬B⇒A, Supposons C, Q, Donc
C⇒A, A».
Exemple 3.2.1
Nous appliquons ces tactiques à la preuve de la formule de
Peirce3.1 :
((p⇒q)⇒p)⇒p. Cette formule n'est pas
prouvable en logique intuitionniste, qui est, ainsi qu'il est dit au
début du chapitre, la logique classique privée de la règle de
réduction à l'absurde. Nous pouvons montrer, qu'en logique
intuitionniste, cette formule est équivalente à la loi du
tiers-exclu.
Vu la forme de la formule, nous devons appliquer la
tactique 5. La preuve de la formule de Peirce
est donc de la forme suivante :
|
Preuve Q : |
| Supposons
(p⇒q)⇒p |
|
Q1 preuve de p dans l'environnement
(p⇒q)⇒p |
|
| Donc
((p⇒q)⇒p)⇒p |
|
Preuve Q1 : |
|
Q11 = P2 où P2 est la preuve de
¬B∨C dans
l'environnement
B⇒C, voir exercice 56 |
|
| Supposons ¬B |
|
Q12 preuve de A = p dans l'environnement ¬B |
|
| Donc
¬B⇒A |
| Supposons C |
|
Q13 preuve de A = p dans l'environnement C |
|
| Donc
C⇒A |
|
A |
Q12 est la preuve
de C = p dans l'environnement
¬(p⇒q).
Puisque
¬A est une abréviation de
A⇒ , cette preuve est
la preuve P6 demandée à l'exercice 56, où B = p et C = q. En recollant les morceaux
Q1, Q11, Q12, Q13, nous
obtenons la preuve Q, que nous ne recopions pas ici, car elle peut
être obtenue automatiquement par le logiciel développé par Michel
Levy, disponible à l'adresse suivante :
http://teachinglogic.liglab.fr/DN/
, cette preuve est
la preuve P6 demandée à l'exercice 56, où B = p et C = q. En recollant les morceaux
Q1, Q11, Q12, Q13, nous
obtenons la preuve Q, que nous ne recopions pas ici, car elle peut
être obtenue automatiquement par le logiciel développé par Michel
Levy, disponible à l'adresse suivante :
http://teachinglogic.liglab.fr/DN/
Nous montrons ci-dessous comme retrouver la preuve Q12 sans
utiliser les tactiques. La seule règle, ne conduisant pas à une
impasse, est la réduction à l'absurde. Donc cette preuve est de la
forme :
|
Preuve Q12 de p dans l'environnement
¬(p⇒q) |
| Supposons ¬p |
Q121 preuve de  dans l'environnement
¬(p⇒q), ¬p dans l'environnement
¬(p⇒q), ¬p |
|
| Donc
¬¬p |
|
p |
 , il faut
déduire
p⇒q. Donc la preuve Q121 est :
, il faut
déduire
p⇒q. Donc la preuve Q121 est :
| Supposons p |
 |
|
q |
| Donc
p⇒q |
 |
La preuve de cohérence de la déduction naturelle consiste à montrer
que chaque preuve construite à partir d'un ensemble de formules
Γ donne une formule qui est déductible de Γ.
Théorème 3.3.1 (Cohérence de la déduction)
Si une formule A est déduite d'un environnement de formules Γ
(
Γ  A), alors A est une conséquence de Γ
(
Γ
A), alors A est une conséquence de Γ
(
Γ  A).
A).
Preuve : Soit Γ un ensemble de formules. Soit P une preuve
de A dans cet environnement. Soient Ci la conclusion et Hi
le contexte de la
i ligne de la preuve P. Notons
par
Γ, Hi l'ensemble des formules de l'ensemble Γ
et de la liste Hi. Nous montrons par induction que pour
tout k nous avons
Γ, Hk  Ck, ce qui implique que
pour la dernière ligne n de cette preuve, comme par définition
Hn est la liste vide et Cn = A, nous obtenons
Γ
Ck, ce qui implique que
pour la dernière ligne n de cette preuve, comme par définition
Hn est la liste vide et Cn = A, nous obtenons
Γ  A.
A.
- Case de base :
- Supposons que A est déduite de Γ par la
preuve vide. Alors A est élément de
Γ, donc
Γ
 A.
A.
- Induction :
- Supposons que pour toute ligne i < k de la preuve
nous avons
Γ, Hi
 Ci. Montrons que
Γ, Hk
Ci. Montrons que
Γ, Hk  Ck. Supposons que la ligne k est :
Ck. Supposons que la ligne k est :
- «Supposons Ck». La formule Ck est la
dernière formule de Hk, donc
Γ, Hk
 Ck.
Ck.
- «Donc Ck». La formule Ck est égale
à la formule
B⇒D, et B est la
dernière formule de Hk-1. Nous distinguons deux cas, soit D
est élément de Γ, soit D est
utilisable sur la ligne précédente.
- Dans le premier cas, puisque D est égale à une
formule de Γ, D est conséquence de Γ donc de
Γ, Hk.
Puisque
B⇒D est conséquence de D, il en résulte que
Γ, Hk
 Ck
Ck
- Dans le deuxième cas, D est utilisable sur la ligne
précédente. Donc il existe i < k tel que D = Ci et Hi est
préfixe de Hk-1. Par hypothèse de récurrence,
Γ, Hi
 D. Puisque Hi est préfixe de Hk-1, nous avons
Γ, Hk-1
D. Puisque Hi est préfixe de Hk-1, nous avons
Γ, Hk-1  D. Puisque B est la dernière formule de
Hk-1, nous avons
Hk-1 = Hk, B et donc
Γ, Hk, B
D. Puisque B est la dernière formule de
Hk-1, nous avons
Hk-1 = Hk, B et donc
Γ, Hk, B  D, ce qui implique
Γ, Hk
D, ce qui implique
Γ, Hk  B⇒D.
Enfin puisque Ck est égale à
B⇒D et que deux formules égales sont
équivalentes, nous avons
Γ, Hk
B⇒D.
Enfin puisque Ck est égale à
B⇒D et que deux formules égales sont
équivalentes, nous avons
Γ, Hk  Ck.
Ck.
- «Ck». Cette formule est la conclusion d'une règle de la
table 3.1, appliquée à ses prémisses utilisables à la
ligne précédente ou aux éléments de Γ. Considérons le seul
cas de la règle ∧I, les autres cas étant analogues. La
formule Ck est égale à
(D∧E) et les prémisses de la
règle sont D et E. Puisque D et E sont éléments de Γ
ou utilisables à la ligne précédente, comme dans le cas précédent,
en utilisant l'hypothèse de récurrence, nous avons :
Γ, Hk-1
 D et
Γ, Hk-1
D et
Γ, Hk-1  E. Puisque la ligne k ne change pas les hypothèses, nous avons
Hk-1 = Hk, donc
Γ, Hk
E. Puisque la ligne k ne change pas les hypothèses, nous avons
Hk-1 = Hk, donc
Γ, Hk  D et
Γ, Hk
D et
Γ, Hk  E. Puisque Ck est égale à
(D∧E), nous avons :
D, E
E. Puisque Ck est égale à
(D∧E), nous avons :
D, E  Ck. Par suite
Γ, Hk
Ck. Par suite
Γ, Hk  Ck.
Ck.

Nous prouvons la complétude des règles uniquement pour les formules
avec les symboles logiques
 , ∧, ∨, ⇒. La
complétude pour les formules obtenues en ajoutant les symboles
logiques
, ∧, ∨, ⇒. La
complétude pour les formules obtenues en ajoutant les symboles
logiques  , ¬ et
⇔ résulte immédiatement du
fait que ces symboles peuvent être considérés comme des abréviations.
, ¬ et
⇔ résulte immédiatement du
fait que ces symboles peuvent être considérés comme des abréviations.
Vu l'absence de négation, nous définissons un littéral comme étant
une variable ou une implication entre une variable et  . Soit
x une variable, x et
x⇒
. Soit
x une variable, x et
x⇒ (qui peut être abrégé
en ¬x) sont des littéraux complémentaires. Dans la suite nous
distinguons une liste de formules Γ et s(Γ) l'ensemble
des formules de la liste. Pour simplifier les notations, nous
utilisons la virgule pour ajouter un élément en début ou en fin de
liste ainsi que pour concaténer deux listes, que ces listes soit des
listes de formules ou des preuves.
(qui peut être abrégé
en ¬x) sont des littéraux complémentaires. Dans la suite nous
distinguons une liste de formules Γ et s(Γ) l'ensemble
des formules de la liste. Pour simplifier les notations, nous
utilisons la virgule pour ajouter un élément en début ou en fin de
liste ainsi que pour concaténer deux listes, que ces listes soit des
listes de formules ou des preuves.
Théorème 3.4.1
Soient Γ un ensemble fini de formules et A une formule, si
Γ  A alors
Γ
A alors
Γ  A.
A.
Preuve : Soit m une mesure des formules et des listes de formules, ainsi définie :
-
m(
 ) = 0,
) = 0,
- m(x) = 1 où x est une variable,
-
m(⇒) = 1,
-
m(∧) = 1,
- m(∨) = 2,
-
m(AoB) = m(A) + m(o) + m(B),
- la mesure d'une liste de formules est la somme des mesures des
formules de la liste.
Puisque les formules ¬A et
A⇒ sont égales aux
abréviations près, nous avons :
m(¬A) = m(A⇒
sont égales aux
abréviations près, nous avons :
m(¬A) = m(A⇒ ) = m(A) + 1. Par exemple soit
A = (a∨¬a). nous avons
m(¬a) = 2, m(A) = 5 et
m(A, (b∧b), A) = 13.
) = m(A) + 1. Par exemple soit
A = (a∨¬a). nous avons
m(¬a) = 2, m(A) = 5 et
m(A, (b∧b), A) = 13.
Soit P(n) la propriété suivante : soient Γ une liste de
formules et A une formule telles que la mesure de la liste
Γ, A est n, si
s(Γ)  A alors
s(Γ)
A alors
s(Γ)  A.
A.
Supposons que pour tout i < k, la propriété P(i) est
vérifiée. Supposons que
m(Γ, A) = k et que
s(Γ)  A. Pour prouver P(k), donc aussi P(n) pour tout n, il suffit
de montrer que :
s(Γ)
A. Pour prouver P(k), donc aussi P(n) pour tout n, il suffit
de montrer que :
s(Γ)  A.
Nous posons que A est indécomposable si A est
A.
Nous posons que A est indécomposable si A est  ou
une variable, et Γ est indécomposable si Γ est une
liste de littéraux ou comprend la formule
ou
une variable, et Γ est indécomposable si Γ est une
liste de littéraux ou comprend la formule  . Nous étudions trois
cas :
. Nous étudions trois
cas :
- Cas 1 :
- ni A, ni Γ ne sont
décomposables.
- Cas 2 :
- A est décomposable. Nous décomposons A en deux
sous-formules B et C, nous obtenons les inégalités suivantes :
m(Γ, B) < m(Γ, A) et
m(Γ, C) < m(Γ, A). Ainsi nous
appliquons l'hypothèse de récurrence puis nous concluons.
- Cas 3 :
- Γ est décomposable. Nous permutons Γ afin
d'obtenir une liste et une formule décomposable.
Ainsi nous appliquons l'hypothèse de récurrence à la formule puis nous
concluons.
- Cas 1 :
- Lorsqu'il est impossible de décomposer A et
Γ, alors A est
 ou une variable et Γ
est une liste de littéraux ou comprend la formule
ou une variable et Γ
est une liste de littéraux ou comprend la formule  . Nous
distinguons deux cas :
. Nous
distinguons deux cas :
- (a)
- Soit
 est une formule de Γ alors A peut se
déduire de
est une formule de Γ alors A peut se
déduire de  par la règle Efq, donc
s(Γ)
par la règle Efq, donc
s(Γ)  A.
A.
- (b)
- Soit
 n'est pas une formule de Γ. Donc,
Γ est une liste de littéraux et nous avons deux possibilités
:
n'est pas une formule de Γ. Donc,
Γ est une liste de littéraux et nous avons deux possibilités
:
- A =
 . Puisque
s(Γ)
. Puisque
s(Γ)  A, la liste Γ
comporte deux littéraux complémentaires, donc A peut se déduire de
Γ par la règle
⇒E, et par suite
s(Γ)
A, la liste Γ
comporte deux littéraux complémentaires, donc A peut se déduire de
Γ par la règle
⇒E, et par suite
s(Γ)  A (par la preuve
A (par la preuve  , A).
, A).
- A est une variable. Puisque
s(Γ)
 A :
A :
- soit
Γ comporte deux littéraux complémentaires et comme dans le
cas précédent, nous avons
s(Γ)
 A
A
- soit A est élément
de Γ et dans ce cas nous avons aussi
s(Γ)
 A (par
la preuve vide).
A (par
la preuve vide).
- Cas 2 :
- A est décomposable.
- (c)
- Supposons que
A = (B∧C). Nous savons que
s(Γ)
 B et
s(Γ)
B et
s(Γ)  C. Les mesures de B et C sont
strictement inférieures à celles de A. Donc
m(Γ, B) < k et
m(Γ, C) < k, et par hypothèse de récurrence, il existe
deux preuves P et Q telles que
s(Γ)
C. Les mesures de B et C sont
strictement inférieures à celles de A. Donc
m(Γ, B) < k et
m(Γ, C) < k, et par hypothèse de récurrence, il existe
deux preuves P et Q telles que
s(Γ)  P : B et
s(Γ)
P : B et
s(Γ)  Q : C. Puisque A peut se déduire de B et C
par la règle ∧I : «
P, Q, A» est une preuve de A dans
l'environnement s(Γ) donc
s(Γ)
Q : C. Puisque A peut se déduire de B et C
par la règle ∧I : «
P, Q, A» est une preuve de A dans
l'environnement s(Γ) donc
s(Γ)  A.
A.
- (d)
- Supposons que
A = (B⇒C). Puisque
s(Γ)
 A, il en résulte que
s(Γ, B)
A, il en résulte que
s(Γ, B)  C. La somme des
mesures de B et C est strictement inférieure (de 1) à celle de
A. Donc
m(Γ, B, C) < k, et par hypothèse de
récurrence, il existe une preuve P telle que
s(Γ, B)
C. La somme des
mesures de B et C est strictement inférieure (de 1) à celle de
A. Donc
m(Γ, B, C) < k, et par hypothèse de
récurrence, il existe une preuve P telle que
s(Γ, B)  P : C. Puisque nous pouvons déduire A de C en appliquant
la règle
⇒I qui enlève l'hypothèse B :
«
SupposonsB, P, DoncA» est une preuve de
A dans l'environnement s(Γ) donc
s(Γ)
P : C. Puisque nous pouvons déduire A de C en appliquant
la règle
⇒I qui enlève l'hypothèse B :
«
SupposonsB, P, DoncA» est une preuve de
A dans l'environnement s(Γ) donc
s(Γ)  A.
A.
- (e)
- Supposons que
A = (B∨C). Puisque
s(Γ)
 A, il en résulte que
s(Γ, ¬B)
A, il en résulte que
s(Γ, ¬B)  C.
C.
Puisque
m(A) = m(B) + m(C) + 2 et que
m(¬B) = m(B) + 1 , la somme des mesures
de ¬B et de C est strictement inférieure (de 1) à celle de
A. Donc
m(Γ, ¬B, C) < k, et par hypothèse de
récurrence, il existe une preuve P telle que
s(Γ, ¬B)  P : C.
P : C.
Soit P1 (cette preuve est demandée à
l'exercice 56) une preuve de B∨C dans l'environnement
¬B⇒C.
Puisque nous pouvons déduire
¬B⇒C de C en appliquant la règle
⇒I qui
enlève l'hypothèse ¬B :
«
Supposons¬B, P, Donc¬B⇒C, P1» est une preuve
de A dans l'environnement s(Γ), donc
s(Γ)  A.
A.
- Cas 3 :
- Γ est décomposable. Par définition, toute
permutation de Γ a la même mesure que Γ. La liste
Γ est une permutation d'une des listes suivantes :
- (f)
-
(B∧C), Δ. Puisque
s(Γ)
 A, il
en résulte que
s(B, C, Δ)
A, il
en résulte que
s(B, C, Δ)  A. La somme des mesures
de B et C est strictement inférieure (de 1) à celle de
B∧C. Donc
m(B, C, Δ, A) < m((B∧C), Δ, A) = m(Γ, A) = k. Par hypothèse de récurrence, il existe
une preuve P telle que
s(B, C, Δ)
A. La somme des mesures
de B et C est strictement inférieure (de 1) à celle de
B∧C. Donc
m(B, C, Δ, A) < m((B∧C), Δ, A) = m(Γ, A) = k. Par hypothèse de récurrence, il existe
une preuve P telle que
s(B, C, Δ)  P : A. Puisque
B peut se déduire de
B∧C par la règle ∧E1 et que
C peut se déduire de
B∧C par la règle ∧E2 : «
B, C, P» est une preuve de A dans l'environnement
s(Γ), donc
s(Γ)
P : A. Puisque
B peut se déduire de
B∧C par la règle ∧E1 et que
C peut se déduire de
B∧C par la règle ∧E2 : «
B, C, P» est une preuve de A dans l'environnement
s(Γ), donc
s(Γ)  A.
A.
- (g)
-
(B∨C), Δ. Puisque
s(Γ)
 A, il en
résulte que
s(B, Δ)
A, il en
résulte que
s(B, Δ)  A et
s(C, Δ)
A et
s(C, Δ)  A. Les mesures des formules B et C sont strictement inférieures
à celle de B∨C. Donc
m(B, Δ, A) < k et
m(C, Δ, A) < k. Par hypothèse de récurrence, il existe deux preuves P
et Q telles que
s(B, Δ)
A. Les mesures des formules B et C sont strictement inférieures
à celle de B∨C. Donc
m(B, Δ, A) < k et
m(C, Δ, A) < k. Par hypothèse de récurrence, il existe deux preuves P
et Q telles que
s(B, Δ)  P : A et
s(C, Δ)
P : A et
s(C, Δ)  Q : A.
Q : A.
Puisque A peut se déduire de B∨C,
B⇒A,
C⇒A par la règle ∨E :
«
SupposonsB, P, DoncB⇒A, SupposonsC, Q, DoncC⇒A, A» est une preuve de
A dans l'environnement s(Γ), donc
s(Γ)  A.
A.
- (h)
-
(B⇒C), Δ où
C
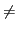
 . Puisque
s(Γ)
. Puisque
s(Γ)  A, il en résulte que
s(¬B, Δ)
A, il en résulte que
s(¬B, Δ)  A et
s(C, Δ)
A et
s(C, Δ)  A. Comme
C
A. Comme
C 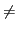
 , la mesure de
C n'est pas nulle et donc
m(¬B) < m(B⇒C). Il est clair que :
m(C) < m(B⇒C). Par suite
m(¬B, Δ, A) < k et
m(C, Δ, A) < k, donc
par hypothèse de récurrence, il existe deux preuves P et
Q telles que
s(¬B, Δ)
, la mesure de
C n'est pas nulle et donc
m(¬B) < m(B⇒C). Il est clair que :
m(C) < m(B⇒C). Par suite
m(¬B, Δ, A) < k et
m(C, Δ, A) < k, donc
par hypothèse de récurrence, il existe deux preuves P et
Q telles que
s(¬B, Δ)  P : A et
s(C, Δ)
P : A et
s(C, Δ)  Q : A.
Q : A.
Soit P2 (la preuve P2 est demandée à
l'exercice 56) une preuve de
¬B∨C
dans l'environnement
B⇒C. Puisque A peut se déduire
de
¬B∨C,
¬B⇒A,
C⇒A par la règle ∨E :
«
P2, Supposons¬B, P, Donc(¬B⇒A), SupposonsC, Q, Donc(C⇒A), A» est une preuve de A
dans l'environnement s(Γ), donc
s(Γ)  A.
A.
- (i)
-
¬(B∧C), Δ. Puisque
s(Γ)
 A, il en résulte que
s(¬B, Δ)
A, il en résulte que
s(¬B, Δ)  A et
s(¬C, Δ)
A et
s(¬C, Δ)  A.
Les mesures de ¬B et de ¬C sont strictement
inférieures à celle de
¬(B∧C). Donc
m(¬B, Δ, A) < k et
m(¬C, Δ, A) < k, par
hypothèse de récurrence, il existe deux preuves P et Q
telles que
s(¬B, Δ)
A.
Les mesures de ¬B et de ¬C sont strictement
inférieures à celle de
¬(B∧C). Donc
m(¬B, Δ, A) < k et
m(¬C, Δ, A) < k, par
hypothèse de récurrence, il existe deux preuves P et Q
telles que
s(¬B, Δ)  P : A et
s(¬C, Δ)
P : A et
s(¬C, Δ)  Q : A.
Q : A.
Soit P3 (la
preuve P3 est demandée à l'exercice 56) une preuve de
¬B∨¬C dans l'environnement
¬(B∧C).
Puisque A peut se déduire de
¬B∨¬C,
¬B⇒A,
¬C⇒A par la
règle ∨E :
«
P3, Supposons¬B, P, Donc¬B⇒A, Supposons¬C, Q, Donc¬C⇒A, A» est une preuve de A dans
l'environnement s(Γ), donc
s(Γ)  A.
A.
- (j)
-
¬(B∨C), Δ. Puisque
s(Γ)
 A,
il en résulte que
s(¬B, ¬C, Δ)
A,
il en résulte que
s(¬B, ¬C, Δ)  A.
A.
Puisque
la mesure de ∨ est 2, la somme des mesures de ¬B et de
¬C est strictement inférieure (de 1) à celle de
¬(B∨C). Donc
m(¬B, ¬C, Δ, A) < k, par hypothèse
de récurrence, il existe une preuve P telle que :
s(¬B, ¬C, Δ)  P : A.
P : A.
Soit P4 une preuve de ¬B dans l'environnement
¬(B∨C) et P5 une preuve de
¬C dans ce même environnement (les preuves P4 et P5 sont
demandées à l'exercice 56) :
«
P4, P5, P» est
une preuve de A dans l'environnement s(Γ), donc
s(Γ)  A.
A.
- (k)
-
¬(B⇒C), Δ. Puisque
s(Γ)
 A, il en résulte que
s(B, ¬C, Δ)
A, il en résulte que
s(B, ¬C, Δ)  A. La somme des mesures de B et de ¬C est inférieure de 1 à
celle de
¬(B⇒C).
Donc
m(B, ¬C, Δ, A) < k, et par hypothèse de récurrence, il existe une preuve P
telle que :
s(B, ¬C, Δ)
A. La somme des mesures de B et de ¬C est inférieure de 1 à
celle de
¬(B⇒C).
Donc
m(B, ¬C, Δ, A) < k, et par hypothèse de récurrence, il existe une preuve P
telle que :
s(B, ¬C, Δ)  P : A.
P : A.
Soient P6 une preuve de B dans l'environnement
¬(B⇒C) et P7 une preuve de ¬C dans ce même environnement (les preuves
P6 et P7 sont demandées à l'exercice 56) :
«
P6, P7, P» est une preuve de A dans l'environnement
s(Γ), donc
s(Γ)  A.
A.

Remarque 3.4.2
La preuve de complétude est constructive, c'est-à-dire qu'elle donne
un ensemble complet de tactiques pour construire des preuves d'une
formule dans un environnement. Cependant ces tactiques peuvent donner
des preuves longues. En particulier si nous devons prouver une
formule
(B∨C), il vaut mieux en général suivre les tactiques
données au paragraphe 3.2, c'est-à-dire essayer de
prouver B, puis essayer de prouver C et seulement en cas
d'échec, utiliser la tactique donnée dans la preuve de complétude,
qui «réduit» cette preuve à une preuve de C en ajoutant
l'hypothèse ¬B.
3.5 Outils
Nous indiquons deux logiciels pour se familiariser avec la déduction
naturelle. Le premier construit automatiquement des preuves comme
nous les avons présentées, le deuxième illustre sur quelques
exemples de manière interactive comment dessiner des preuves sous
forme d'arbres.
Pour produire automatiquement des preuves, nous recommandons
d'utiliser le logiciel :
Ce logiciel permet grâce à une syntaxe intuitive de saisir une
formule et de générer automatiquement :
- si la formule est (syntaxiquement) incorrecte, un message
d'erreur (en rouge) est produit au dessus de la formule
- si la formule est prouvable, sa preuve (sans annotation) est
générée par le logiciel.
- si la formule est correcte mais n'est pas prouvable, un
contre-modèle est proposé au dessus de la formule.
Si la formule est prouvable, il est aussi possible d'obtenir une
version de la preuve annotée.
Ceux qui affectionnent les preuves sous forme d'arbres peuvent
utiliser le logiciel suivant développé Laurent
Théry :
Ce logiciel se présente comme un jeu, il propose des formules à
prouver et permet d'appliquer les règles de la déduction
naturelle, de manière interactive, pour en construire les arbres de
preuve. Quand vous réussissez à construire la preuve d'une formule,
vous voyez la photo de Dag Prawitz, un des
principaux logiciens qui a étudié les propriétés de la déduction
naturelle.




suivant: II. Logique du premier
monter: I. Logique propositionnelle
précédent: 2. Résolution propositionnelle
Table des matières
Index
Benjamin Wack
2013-01-08
![$\displaystyle \infer[R]{C} {H_1 \ldots H_n}$](img79.png)
![$\displaystyle \infer[\wedge I]{A \wedge B}{A & B}$](img80.png)
![$\displaystyle \infer[\wedge E1]{A}{A \wedge B} \qquad \infer[\wedge E2]{B}{A \wedge B}$](img81.png)
![$\displaystyle \infer[\vee I1]{A \vee B}{A} \qquad \infer[\vee I2]{B \vee A}{A}$](img82.png)
![$\displaystyle \infer[\vee E]{C}{A \vee B & A \Rightarrow C & B \Rightarrow C }$](img83.png)
![$\displaystyle \infer[\Rightarrow E]{B}{A & A \Rightarrow B}$](img84.png)
![$\displaystyle \infer[\Rightarrow I]{ A \Rightarrow B}{\infer*{B}{[A]}}$](img85.png)
![$\displaystyle \infer[Efq]{A}{\bot}$](img86.png)
![$\displaystyle \infer[RAA]{A}{\neg \neg A}$](img87.png)
![]() A le fait qu'il y a une preuve de A dans
l'environnement Γ et
Γ
A le fait qu'il y a une preuve de A dans
l'environnement Γ et
Γ ![]() P : A le fait que P est
une preuve de A dans l'environnement Γ. Lorsque
l'environnement est vide, nous l'omettons, autrement dit nous
abrégeons
∅
P : A le fait que P est
une preuve de A dans l'environnement Γ. Lorsque
l'environnement est vide, nous l'omettons, autrement dit nous
abrégeons
∅ ![]() A en
A en ![]() A. Lorsque nous demandons
une preuve d'une formule sans indiquer d'environnement, nous supposons
que l'environnement est vide.
A. Lorsque nous demandons
une preuve d'une formule sans indiquer d'environnement, nous supposons
que l'environnement est vide.
![]() et ¬A ainsi que
(¬A∨B)⇒
et ¬A ainsi que
(¬A∨B)⇒![]() et
¬(¬A∨B).
et
¬(¬A∨B).
![]() Ck, ce qui implique que
pour la dernière ligne n de cette preuve, comme par définition
Hn est la liste vide et Cn = A, nous obtenons
Γ
Ck, ce qui implique que
pour la dernière ligne n de cette preuve, comme par définition
Hn est la liste vide et Cn = A, nous obtenons
Γ ![]() A.
A.
![]() , ∧, ∨, ⇒. La
complétude pour les formules obtenues en ajoutant les symboles
logiques
, ∧, ∨, ⇒. La
complétude pour les formules obtenues en ajoutant les symboles
logiques ![]() , ¬ et
⇔ résulte immédiatement du
fait que ces symboles peuvent être considérés comme des abréviations.
, ¬ et
⇔ résulte immédiatement du
fait que ces symboles peuvent être considérés comme des abréviations.
![]() . Soit
x une variable, x et
x⇒
. Soit
x une variable, x et
x⇒![]() (qui peut être abrégé
en ¬x) sont des littéraux complémentaires. Dans la suite nous
distinguons une liste de formules Γ et s(Γ) l'ensemble
des formules de la liste. Pour simplifier les notations, nous
utilisons la virgule pour ajouter un élément en début ou en fin de
liste ainsi que pour concaténer deux listes, que ces listes soit des
listes de formules ou des preuves.
(qui peut être abrégé
en ¬x) sont des littéraux complémentaires. Dans la suite nous
distinguons une liste de formules Γ et s(Γ) l'ensemble
des formules de la liste. Pour simplifier les notations, nous
utilisons la virgule pour ajouter un élément en début ou en fin de
liste ainsi que pour concaténer deux listes, que ces listes soit des
listes de formules ou des preuves.
![]() A alors
s(Γ)
A alors
s(Γ) ![]() A.
A.
![]() A. Pour prouver P(k), donc aussi P(n) pour tout n, il suffit
de montrer que :
s(Γ)
A. Pour prouver P(k), donc aussi P(n) pour tout n, il suffit
de montrer que :
s(Γ) ![]() A.
Nous posons que A est indécomposable si A est
A.
Nous posons que A est indécomposable si A est ![]() ou
une variable, et Γ est indécomposable si Γ est une
liste de littéraux ou comprend la formule
ou
une variable, et Γ est indécomposable si Γ est une
liste de littéraux ou comprend la formule ![]() . Nous étudions trois
cas :
. Nous étudions trois
cas :
![]()