 |
|
Dans ce cours nous nous intéresserons uniquement à la preuve de la correction partielle des programme.
Les principes qui permettent de prouver la correction partielle d'un programme sont issus des travaux de Robert W. Floyd, C.A.R. Hoare et Edsger W. Dijkstra principalement entre 1969 et 1974.

C'est un programme qui fait ce qu'il est censé faire.

Mais comment exprimer ce qu'il est censé faire?

En exprimant ce qu'on attend du résultat du programme sous la forme de propriétés.
Rappel : Étant donné deux entiers naturels $A,B\in\mathbb{N}$, l'entier $A$ peut s'écrire sous la forme
Algorithme de la division euclidienne : Considérons un programme de division euclidienne qui prend en paramètre deux entiers $A$ et $B$ et qui calcule les valeurs de $r$ et $q$ représentant respectivement le reste et le quotient de $A$ par $B$.
r:=A ; q:=0 ;
while(r >= B){
r:=r-B ;
q:=q+1 ;
}
Si le programme est correct, en sortie
les variables $r$ et $q$ doivent satisfaire l'équation
$A = B \times q + r \textit{ avec } 0\leq r< B$
 |
|

S'il vous plaît, ne prononcez plus jamais le mot "dém..." ou "pr...", \ca me donne mal à la tête.
Dans ce cours on ne s'intéressera pas à la terminaison des programmes.
Mais si on voulait garantir la terminaison de l'algorithme de division euclidienne,
quelles les conditions devraient satisfaire les paramètres $A$ et $B$ ?
Considérons l'algorithme DIV de division euclidienne qui prend en paramètre deux entiers $A$ et $B$ et qui calcule les valeurs des entiers $r$ et $q$ représentant respectivement le reste et le quotient de $A$ par $B$.
r:=A ; q:=0 ;
while(r >= B){
r:=r-B ;
q:=q+1 ;
}
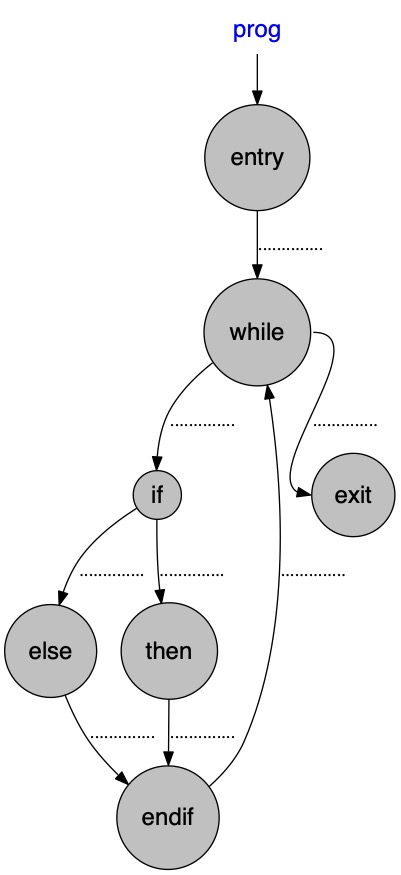
Il est assez aisé d'obtenir une version graphique du graphe de contrôle d'un programme (abbrégé en CFG, de l'anglais Control Flow Graph).
Considérons le programme :
P0;
while (C1) {
if (C2)
then P1
else P2 ;
P3
}
On décrit chacune des transitions au format .dot :
On peut redéfinir les noms des noeuds et leur apparenceprog -> entry; entry -> while [label = "P0"]; while -> if [label = "C1"]; while -> exit [label = "not C1"]; if -> then [label = "C2"]; if -> else [label = "not C2"]; then -> endif [label = "P1"]; else -> endif [label = "P2"]; endif -> while [label="P3"];
node [shape=plaintext, fontname=comic, fontsize=18, fontcolor=blue]; prog [label="automate"]; node [shape=circle, peripheries=1, style=filled, color=black, fillcolor=gray, fontcolor=black]; entry [label="Q0"]; while [label="Qw"]; if [label="Qif"]; then [label="Qt"]; else [label="Qe"]; endif [label="Qfi"]; exit [label="Qs" ];
On réorganise les informations précédentes et on l'enregistre dans un fichier .dot
digraph cfg{
// NAME
node [shape=plaintext, fontname=comic, fontsize=18, fontcolor=blue];
prog;
// STATES
node [shape=circle, peripheries=1, style=filled, color=black, fillcolor=gray, fontcolor=black];
entry;
while;
if;
then;
else;
endif;
exit;
// TRANSITIONS
prog -> entry ;
entry -> while [label = ".............. "];
while:e -> exit:w [label = ".............. "];
while -> if [label = ".............. "];
if -> then [label = ".............. "];
then -> endif [label = ".............. "];
if -> else [label = ".............. "];
else -> endif [label = ".............. "];
endif -> while [label = ".............. "];
}
L'outil graphviz permet de visualier le fichier .dot
et d'exporter le graphique dans différents formats .pdf, .jpg.

C'est avec cet outil que je génère les dessins d'automates.
Installez le et essayez le.
Pour l'instant nous avons utilisé uniquement deux types d'instructions :
Ils peuvent tous être réalisés avec des transitions test qui portent la condition de branchement.
Il reste à voir deux instructions qui effectuent un saut inconditionnel.
Grâce à l'instruction return il est possible d'interrompre une boucle et de sauter directement dans l'état de sortie de l'automate.
Les traductions proposées pour les 2 programmes suivants sont-elles correctes ?
| P1 | P2 |
|---|---|
x:=1 ; |
x:=x+1 ; |

Lorsque deux affectations sont indépendantes, l'ordre dans lesquel les effectuer n'a pas d'importance et
on peut même les effectuer en parallèle.
Il y a une dépendance entre deux affectations $x:=e_1$ et $y:=e_2$
lorsque la valeur de la partie droite ($e_1$ ou $e_2$) de l'une d'elle dépend
de la variable ($x$ ou $y$) de l'autre.
Dans ce cas l'ordre dans lequel on effectue les affectations a de l'importance
et on ne doit pas regrouper les deux affectations sur la même transition.
Voici le graphe de flot de contrôle du programme
x:=1 ; y:=x+1 ; z:=y+1

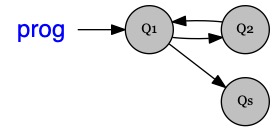
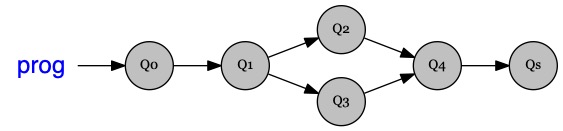
Consigne : Dessinez le GFC associé à chacun des programmes ci-dessous
if (x<0) then x:=1 else x:=2 ; x:=x+1
while (x<0) { x:=x+1 }
do { x:=x+1 } until (x>1)
while (true) { if (x<0) then x:=x+1 else return }
Pour vous aidez on donne (dans le désordre) la structure des différents GFCs ; il n'y en a que 3 et c'est normal.
|
|
|
|
Question : Combien en avez-vous dessiné dont vous êtes sûr ?
1? 2? 3? 4?
 |
|
Pour prouver qu'un programme est correct, on doit énoncer les propriétés qu'il est censé respecter et les associer aux états de l'automate.
Exemple : Dans le cas de la division euclidienne, les propriétés qui nous intéressent sont :
 |
|
L'automate DIV est une version compilée de l'algorithme de division euclidienne.
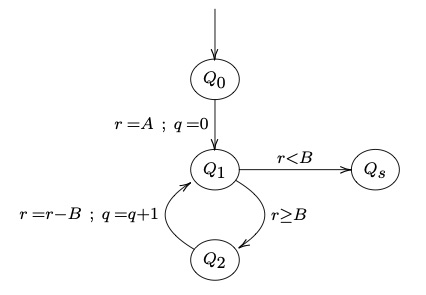
Pour exécuter l'algorithme, on commence dans l'état $Q_0$ avec des valeurs pour les paramètres, par exemple $A = 8$ et $B = 3$.
On passe de l'état courant à un autre en empruntant une transition :
| condition | propriété | propriété | |||
|---|---|---|---|---|---|
| état | ~~$q$~~ | ~~$r$~~ | $r< B$ | $A=B \times q + r$ | $0\leq r$ |
| $Q_0$ | |||||
| $Q_1$ | 0 | 8 | F | V | V |
| $Q_2$ | 0 | 8 | F | V | V |
| $Q_1$ | 1 | 5 | F | V | V |
| $Q_2$ | 1 | 5 | F | V | V |
| $Q_1$ | 2 | 2 | V | V | V |
| $Q_s$ | 2 | 2 | V | V | V |
On associe à chacun des états $Q_i$ de l'automate, une propriété $\psi_i$ dite invariante, au sens où
Définitionla propriété $\psi_i$ est vraie à chaque fois que l'exécution du programme passe par l'état $Q_i$.
Exemple :
Définition
La propriété $\psi_s$ associée à l'état de sortie $Q_s$ définit le critère de correction du programme.
 |
|

Mais pour démontrer qu'elles sont satijsfaites nous aurons besoin de nous appuyer
sur les propriétés des autres états au cours de l'exécution.

Et pour que notre raisonnement soit valable pour toutes les exécutions possibles
du programme, il faut que les propriétés qui nous seront utiles
ne dépendent pas du chemin pris par l'exécution.

Elles doivent être invariantes!

Si on parvient à montrer que $\psi_s$ est un invariant de $Q_s$
alors on aura la garantie que,
lorsque l'exécution du programme atteindra l'état de sortie,
la propriété désirée sera vraie.

Et si on n'atteint jamais l'état de sortie ?
Quelles sont les valeurs de $r$ et $q$ au point d'entrée du programme (état $Q_0$) ?
| condition | propriété | propriété | |||
|---|---|---|---|---|---|
| état | $~q~$ | $~r~$ | $r<B$ | $A =B \times q + r$ | $0\leq r$ |
| $Q_0$ | ? | ? | ? | ? | ? |
| $Q_1$ | 0 | 8 | F | V | V |
| $Q_2$ | 0 | 8 | F | V | V |
| $Q_1$ | 1 | 5 | F | V | V |
| $Q_2$ | 1 | 5 | F | V | V |
| $Q_1$ | 2 | 2 | V | V | V |
| $Q_s$ | 2 | 2 | V | V | V |
Consigne : Associez les propriétés aux états où elles sont invariantes, c'est à dire $vraies$ à toute étape de l'exécution.
|
|

Et si on n'atteint jamais l'état de sortie du programme ?

Cette question fera l'objet d'un test ...
Une fois qu'on a découvert (soit à l'intuition, soit par un raisonnement en arrière),
des propriétés qui nous paraissent susceptibles d'être des invariants (à ce stade on les appelle des candidats),
on doit prouver que ce sont effectivement des invariants.
Étant donné une transition $q \xrightarrow{inst} q'$ de l'automate
et des candidats $\psi$ et $\psi'$ associés aux états
$q$ et $q'$,
la notation sous forme de triplet de Hoare
résume le lien entre $\psi$ et $\psi'$
via la transition $q \xrightarrow{inst} q'$.
\( \{~ \psi ~\} : q \xrightarrow{inst} q' : \{~ \psi' ~\} \)se lit
Un triplet de Hoare établit un lien de conséquence logique entre la propriété de l'état source $q$ et la propriété associée à l'état cible $q'$.
 |
|

Je t'ai un petit peu aidé quand même avec mon article de 1967 "Assigning Meanings to Programs"
Une preuve de programme consiste à démontrer, transition par transition, que tous les liens de conséquence logique sont valides alors les propriétés associées aux états de l'automate formeront une chaîne de causalités logiques où chaque propriété garantit la suivante, depuis la propriété initiale du programme en $Q_0$ jusqu'à la propriété souhaitée en $Q_s$.

Folks, reconnaissez que j'ai quand même considérablement simplifié votre méthode en automatisant le traitement des affectations.
Et je suis le seul à avoir un vrai nom d'informaticien qui contient $ijk$
les variables les plus utilisées en informatique.
En pratique on utilise la propriété cible, $\psi'$ en $q'$, pour déterminer $\psi$ en $q$
et on prend pour $\psi$ la plus faible condition précédente qui garantit que $\psi'$ sera vérifiée.
 |
|
Consigne : Donnez la précondition garantissant que la propriété après l'affectation soit satisfaite.
 |
|

J'aurais tout simplement écrit :

Voyons si vous avez compris la simplicité du calcul de précondition de Dijkstra.
Considérons des expressions mathématiques quelconque $e_1$ et $e_2$, et une propriété logique quelconque $\psi$ - qui peut contenir des fonctions, des opérateurs et des variables $x,y,...$.
Pour que la propriété $\psi$ soit vraie quandil suffit de prendre pour précondition la propriété $\psi$, dans laquelle on remplace chaque occurence de $x$ par $e_1$ et chaque occurence $y$ par $e_2$.
- on a affecté la valeur de l'expression $e_1$ à la variable $x$
- et qu'on a affecté la valeur de $e_2$ à la variable $y$,
 |
|
L'intérêt du calcul de Dijkstra c'est qu'il est valable quelle que soit la complexité de la fomule et des expressions. On peut le résumer ainsi
\( \{~ \psi[ x \leftarrow e_1, y \leftarrow e_2 ] ~\} ~~ x:=e_1, y:=e_2 ~~ \{~ \psi ~\} \)
où $formule ~ [ variable \leftarrow expression ]$ désigne l'opération de substitution qui remplace chaque occurence de la $variable$ par l'$expression$ dans la $formule$.
 |
|

L'ennui c'est que ce sont les humains qui les programment...
Consigne : Appliquez méthodiquement les substitutions pour retrouver le résultat correct.
 |
|
Que faut-il prouver pour valider un triplet ?
Supposons qu'on a choisi d'associer les candidats $\psi$ et $\psi'$ aux états $q$ et $q'$ reliés par une transition $q \xrightarrow{inst} q'$. Ce qui se résume sous la forme du triplet de Hoare.
 |
|

$\psi'$ sera alors un invariant de $q'$

À condition qu'on réussijsse à démontrer que $\psi$ est un invariant de $q$

Yeap! Les propriétés forment une chaîne de conséquences logiques le long d'un chemin d'exécution,
chacune garantissant la suivante.
Le type de preuve diffère selon la nature de l'instruction $inst$. Examinons chacun des cas.
 |
|
si la propriété $\psi$ est vraie en $q$ pour les valeurs des variables dans la mémoire $M$,Ce qui revient à montrer l'implication :
la propriété $\psi'$ est vraie en $q'$ dans la mémoire en $M$ modifiée par l'affectation $v:=e$.
où $\psi'[v\leftarrow e]$ désigne la propriété $\psi'$ dans laquelle on a substitué (c'est à dire remplacé) toutes les occurences de la variable $v$ par $e$. On appelle $[v\leftarrow e]$ une substitution.
Le coup de génie de Dijsktra c'est d'avoir compris que
pour une transition affectation \( \{~\psi~\}~q \xrightarrow{v:=e} q'~\{~\psi'~\} \)
le meilleur choix pour $\psi$ en $q$, pour satisfaire l'implication (1)
c'est de prendre\( \psi \overset{def}{=} \psi'[v\leftarrow e] \)
 |
|
En effet,
si la propriété $\psi$ est vraie en $q$ et qu'on passe la transition (ce qui signifie que la condition du test vaut $vrai$)Le raisonnement précédent s'écrit sous la forme d'une implication
alors la propriété $\psi'$ est vraie en $q'$.
Dans ce raisonnement la mémoire ne joue aucun rôle puisque l'évaluation d'une transition test ne modifie pas les variables : la mémoire $M$ est inchangée entre $q$ et $q'$.
 |
|

À force de pratiquer j'en ai découvert quelques unes.
Je vous les présenterai dans une prochaine leçon.
En attendant voyons si vos intuitions sont bonnes.
On considére des implications de la forme \( \{~ \psi ~\} \land condition \overset{?}{\Longrightarrow} \{~ \psi' ~\} \) issues de transitions test \( \{~ \psi ~\} : q \xrightarrow{condition} q' : \{~ \psi' ~\} \)
Consigne :
Choississez la plus faible condition $\psi$ en pointillés de sorte que l'implication devienne triviale.
Plus difficile :
Deux cas selon la nature de l'instruction $inst$ :
si la propriété $\psi$ est vraie en $q$ pour les valeurs des variables dans la mémoire $M$, alors la propriété $\psi'$ est vraie en $q'$ dans la mémoire $M$ modifiée par l'affectation $v:=e$.Ce qui revient à montrer l'implication :
Exemple de l'effet d'une substitution :
\( \begin{array}{l} \{~ A = B \times q + r,~ 0\leq r ~\} [r\leftarrow (r-B)] \\=~ \{~ A = B \times q + (r-B),~ 0\leq(r-B) ~\} \end{array} \)

Au départ on ne connaît que la propriété souhaitée à l'état de sortie $Q_s$ :
- $\psi_1 : Q_1 \xrightarrow{r< B} Q_s : \underset{connue}{\psi_s}$ est une transition test.
- La propriété $\psi_1$ en $Q_1$ doit donc satisfaire l'implication : \( \psi_1 \land \overset{test}{\overbrace{r< B}} \Longrightarrow \psi_s ~~ie. \)
\( \psi_1 : \left\{\begin{array}{l} ......... \\ ......... \\ ......... \end{array}\right\} \land r< B \Longrightarrow \psi_s : \left\{\begin{array}{l} (1):~~ A = B \times q + r \\ (2):~~ 0 \leq r \\ (3):~~ r< B \end{array}\right\} \)- On choisit de prendre
\( \begin{array}{c} \psi_1 : \left\{\begin{array}{l} (a):~~A = B \times q + r \\ (b):~~ 0\leq r \end{array}\right\} \end{array} \)- L'implication est valide puisque
- $(a) \Rightarrow (1)$
- $(b) \Rightarrow (2)$
- $test \Rightarrow (3)$
 |
|
- La transition \( ~~ \psi_2 : Q_2 \xrightarrow{r:=r-B~;~q:=q+1} Q_1 : \underset{connue}{\psi_1} \) ne fait que des affectations
- Le meilleur choix pour $\psi_2$ est donc
\( \psi_2 \overset{def}{=} \psi_1[ r\leftarrow r-B~;~q \leftarrow q+1] \)- On effectue les substitutions
\( \begin{array}{rcl} \psi_2 &\overset{def}{=}& \psi_1[ r\leftarrow r-B~;~q \leftarrow q+1] \\&=& \left\{\begin{array}{l} A = B \times q + r \\ 0\leq r \end{array}\right\}[ r\leftarrow r-B~;~q \leftarrow q+1] \\&=& \left\{\begin{array}{l} A = B \times (q+1) + (r-B) \\ 0\leq (r-B) \end{array}\right\} \end{array} \)- On obtient par le calcul de précondition de Dijkstra, après simplification
\( \psi_2 : \left\{\begin{array}{l} A = B \times q + r \\ 0\leq (r-B) \end{array}\right\} \)
Vérification de nos choix d'invariants
- $\psi_1 : Q_1 \xrightarrow{r\geq B} Q_2 : \psi_2$ est une transition test.
- Elle doit donc satisfaire l'implication : \( \psi_1 \land \overset{test}{\overbrace{r\geq B}} \overset{?}{\Longrightarrow} \psi_2 ~~ie. \)
\( \psi_1 : \left\{\begin{array}{l} (a):~~ A = B \times q + r \\ (b):~~ 0 \leq r \\ \end{array}\right\} \land r\geq B \Longrightarrow \psi_2 : \left\{\begin{array}{l} (1):~~ A = B \times q + r \\ (2):~~ 0 \leq (r-B) \\ \end{array}\right\} \)- Les propriétés sont fixées par nos choix précédents.
Il s'agit donc de faire la preuve que l'implication est valide, c'est à dire qu'on doit démontrer $(1)$ et $(2)$ à l'aide des propriétés de la prémisse de l'implication (partie gauche de l'implication).
- $(a) \Rightarrow (1)$
- $test \Rightarrow (2)$, puisque (2) est une reformulation équivalente de la condition du test $r \geq B$
- L'implication de l'étape de vérification est valide, donc nos choix pour $\psi_1,\psi_2,\psi_s$ sont bien des invariants.
 |
|

$\psi_1$ garantit $\psi_2$ après la transition $Q_1 \to Q_2$
et $\psi_2$ garantit $\psi_1$ après la transition $Q_2 \to Q_1$,
de sorte que,
tant que le programme reste dans la boucle les invariants $\psi_1$ et $\psi_2$
se garantissent mutuellement.
Lorsque l'exécution sort de la boucle par la transition $Q_1 \to Q_s$,
$\psi_1$ garantit la propriété $\psi_s$ qui nous intéresse en sortie.
Condition d'utilisation du programme
- La transition $Q_0 \xrightarrow{r:=A~;~q:=0} Q_1$ ne fait que des affectations
- Le meilleur choix pour $\psi_0$ est donc
\( \psi_0 \overset{def}{=} \psi_1[ r\leftarrow A~;~q \leftarrow 0] \)- On effectue les substitutions
\( \begin{array}{rcl} \psi_0 &\overset{def}{=}& \psi_1[ r\leftarrow A~;~q \leftarrow 0] \\&=& \left\{\begin{array}{l} A = B \times q + r \\ 0\leq r \end{array}\right\}[ r\leftarrow A~;~q \leftarrow 0] \\&=& \left\{\begin{array}{l} A = B \times 0 + A \\ 0\leq A \end{array}\right\} = \left\{\begin{array}{l} true \\ 0\leq A \end{array}\right\} \end{array} \)- On obtient par le calcul de précondition de Dijkstra, après simplification
\( \psi_0 : \{~ 0\leq A ~\} \)
 |
|

Connaître une égalité $n=e$ est utile dans une preuve car cela permet de remplacer $n$ par $e$ (ou inversement $e$ par $n$),
soit pour simplifier une expression, soit pour faire apparaitre la variable $n$ dans une expression qui parlait de $e$.
Lorsqu'on découvre une égalité invariante dans un état, il faut la noter (et la prouver). Elle facilitera la preuve des autres invariants.
Il est fréquent que la condition de sortie de boucle d'un programme soit une inégalité arithmétique telle que $n \leq e$ où $n$ est un compteur entier et $e$ une expression. Lorsqu'on exécute le programme sur des valeurs concrètes il se peut qu'à la sortie de la boucle, le compteur $n$ soit en fait égal à l'expression $e$. Il est alors utile d'ajouter l'égalité $n=e$ à l'invariant de sortie de boucle afin de faciliter la preuve, mais bien sûr cela à une contre-partie car il faudra prouver l'égalité qu'on vient d'ajouter.
Prouver une égalité : Lorsque l'égalité $n=e$ est associée à l'état cible, $Q'$, d'une transition test de la forme
la plus faible condition en $Q$ qui permet de prouver l'égalité en $Q'$ est l'inégalité opposée $n\geq e$. En effet,
L'invariant clef d'une preuve de programme est celui associé au noeud qui contrôle la boucle, qu'on appele la tête de boucle, notons le $Q$. Les transitions tests qui décident s'il faut continuer ou interrompre la boucle sont attachées à ce noeud. C'est donc par ce noeud
On peut déduire de ces observations plusieurs contraintes sur la propriété $\psi$ associée à $Q$:
Les remarques précédentes sont utiles pour découvrir les invariants en tête des boucles dans les algorithmes de calculs arithmétiques.
Exemple (1) la multiplication na\ive

On parle d'équilibrage de balance
car la variable $r$ augmente à chaque itération
tandis que la variable $n$ diminue
de manière à maintenir l'équilibre entre les termes de gauche et de droite de l'égalité.
Exemple (2) l'exponentation naïve
Exemple (3) l'exponentiation rapide
On cherche un invariant de $Q$, donc une équation générale qui soit valide à chaque passage en $Q$. Il faut donc réussir à obtenir $A^B$ avec $r,x,n$ de sorte que
D'après $(i)$, il faut composer le terme $x^n$ pour obtenir $A^B$ dans le cas $(i)$ ;
et dans le cas $(ii)$ ce terme devient $?^0$ qui vaut 1.
On a déjà déterminé une partie de l'équation $(3)~~ A^B = r ... x^n$.
Il reste à trouver par quel opérateur remplacer les "..."
mais ca ne devrait pas être trop difficile.
Une inégalité stricte entre entiers peut se réécrire sous la forme d'une inégalité large équivalente.
Exemple