Previous Up Next

4  Junction loops


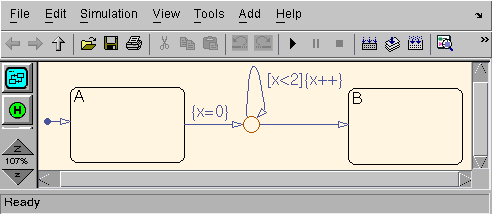
Figure 4: A Stateflow chart with a junction loop

The Stateflow chart shown in Figure 4 (Loops1_docs.mdl) with an observer has a junction loop, the transition labelled [x<2]{x++} initiates a loop in the network. Strictly speaking, we cannot arbitrarily translate this chart into Lustre as it stands since Lustre is compiled into a stackless machine and without a stack it is not possible to implement arbitrary recursion within a reaction. If we try to translate this chart we get: 
% sf2lus Loops1.mdl -o Loops1.lus
Fatal error: exception Failure("Loops found in links")
Detecting loops is trivial. There are two possibilities:
  1. We could give the junction itself a state so that the loop then occurs across synchronous reactions rather than within one.
  2. If we know the loop is bounded, as is the case here, we could unfold the loop into an equivalent one without a loop.

4.1  Junctions as states

The first option is easily implemented in the translator using the -junc_states option: 
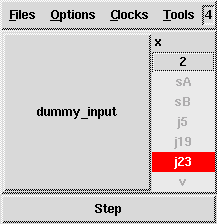
% sf2lus -names -states_visible -junc_states Loops1.mdl -o Loops1.lus
This results in the following sequence when simulated with Luciole:







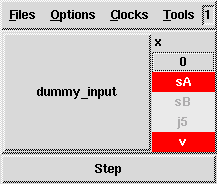
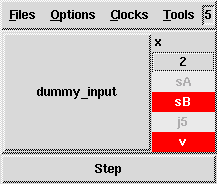
An extra output v has been synthesized (or valid with -full_names) which indicates when the chart is in a state and not a junction. In theory arbitrary recursion could be implemented this way, passing the burden of termination to the client code but it is not a very satisfactory solution.

4.2  Loop unrolling

The sf2lus translator thus supports: First, we add the -counters option to maintain counters on each junction: 
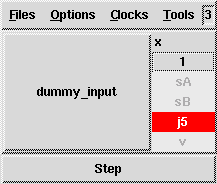
% sf2lus -names -states_visible -junc_states -counters \
         Loops1.mdl -o Loops1.lus
After Luciole simulation we get: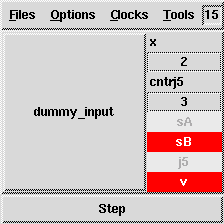



So junction j5 was entered 3 times during execution. We then annotate the junction in the Stateflow chart with the putative loop count maximum. Right-click on the junction, select ``Properties'' and enter: 
cntrlim=3
in the ``Description'' field. With this annotation in place, the -counters option will also cause the translator to output the following observer for the loop counters. The observer node name is comprises loop_counters_<CID> where <CID> is the chart id number as for the toplevel Stateflow: 
-- Observer for junction loop counters
node loop_counters_2(dummy_input: bool) returns(prop: bool);
var x, cntrj5: int; sA, sB, j5, v: bool;
let
  x, cntrj5, sA, sB, j5, v = sf_2(dummy_input);
  prop = cntrj5 <= 3;
tel
which can be passed to Nbac for validation: 
% lus2nbac Loops1.lus loop_counters_2
--Pollux Version 2.1
start normalisation ... done
Bool optimization : 171 -> 96 nodes
start minimal network generation ..... done (96 -> 77 nodes)
% nbacg -analysis 2 loop_counters_2.ba 
...
SUCCESS: property proved
*** END ***
We now have confidence that junction j5 will never be visited more than three time for any possible set of inputs. Thus we can unroll the loop three times: 
% sf2lus -names -states_visible -unroll Loops1.mdl -o Loops1.lus
This results in the following luciole trace which is how one would expect this chart to behave when translated into Lustre:





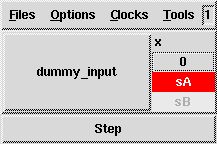
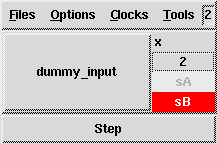
It is perhaps also instructive to add the -junc_states flag which show how the network has been duplicated. Here, the duplicated network appears as junctions j19 and j23:



4.3  Discussion

The technique presented here is quite powerful. We used dynamic profiling (by treating junctions as states) to guess the bounds on the loops. We could then, in theory, use static analysis to unroll the loop into an equivalent one without loops but this is not valid until we have a proof of the bounds on the loops. The Nbac proof bridges this gap and validates the whole process.

However, there are very tight limits upon what can be done given finite resources for translation, proof and static analysis. It is possible that our guessed bounds may not be correct in which case Nbac will fail to provide a proof. It is also possible that Nbac may fail to provide the proof simply on resource limits or the nature of the chart (in general, proofs of this kind are undecidable). Finally, even if we have the proof it is possible that the static analysis can fail on resource limits, for example if the loop bounds were unreasonable.

What has been presented here is simply an example of the kind of analysis available for tackling imperative features of charts. It still depends upon the skill and experience of the chart designer to produce a design which both meets the requirements of the application and of abstract safety properties.

Previous Up Next