Grammaires

Motivation

Ce dernier chapitre est consacré au traitement automatique de données :

lecture du format d'entrée et analyse (parsing),
traitement (calcul et/ou traduction),
génération du résultat dans un format de sortie

Le projet donnera une illustration concrète de cette activité très fréquente chez un informaticien.

Automates, expressions régulières, équations de langages et maintenant les grammaires ...
Mais pourquoi y'a-t'il tant de représentations différentes si elles sont équivalentes ?

Premier élément de réponse :

Les regexp et les grammaires sont la bonne notation pour décrire un langage.
Les automates (AEF, AUP) sont la bonne représentation pour la reconnaissance en raison de leur exécution efficace.

Deuxième élément de réponse : Il existe plusieurs types de grammaires.

Les grammaires régulières sont équivalentes aux AEFs donc aux regexp et ne sont pas très utiles
Les grammaires algébriques sont équivalentes aux AUPs. Elles permettent de décrire plus de langages que les AEFs. Ce sont celles qu'on utilise pour définir/parser les langages de programmation. Elles ont l'avantage de conduire à une exécution efficace via les AUPs. Il faut un parseur efficace (donc déterministe) pour lire la dizaine de millions de lignes de code d'un OS dans le but le compiler.
Il existe d'autres types de grammaires : les grammaires contextuelles (resp. la réecriture libre) qui sont aussi puissantes que les fonctions primitives récursives (resp. que les langages de programmation généralistes).

Troisième élément de réponse : Les grammaires dites à attributs permettent de faire des traitements informatiques (calculs et/ou traduction) pendant la reconnaissance. Les grammaires à attributs forment une catégorie de langages de programmation spécialisés dans le traitement de données : il en existe plusieurs variantes selon l'outil de génération du parseur utilisé (Yacc, Bison, Javacc, AntLR). C'est un concept qu'il faut maîtriser. Vous aurez l'occasion de vous y exercer avec le projet.

Des équations de langages aux grammaires

La même idée a été découverte 4 fois dans des contextes différents :

\(L_1 = a \mathop{\Large.} L_1 \mid b\mathop{\Large.} L_2\), équation de langages, non-orientée (Arden)
\(L_1 \xrightarrow{} a \mathop{\Large.} L_1 \mid b\mathop{\Large.} L_2\), équation orientée pour la génération de phrases (Chomsky, linguiste)
\(L_1 \leftarrow a \mathop{\Large.} L_1 \mid b\mathop{\Large.} L_2\), équation orientée pour reconnaissance (IA en langage Prolog, années 70-80)
\(L_1 ::= a \mathop{\Large.} L_1 \mid a \mathop{\Large.} L_2\), notation de Backus-Naur utilisée dans certains générateurs de parseurs.

Peu importe la notation c'est la même idée. Retenez qu'une grammaire peut-être utilisée dans les deux sens : pour générer des phrases (en composition automatique de littérature ou de musique [*]) ou pour reconnaître/analyser des données en vue d'un traitement informatique. Nous nous intéresserons uniquement au second cas dans ce cours.

[*] En composition automatique on ajoute un modèle probabiliste aux grammaires afin de déclencher la règle de production qui a la plus forte probabilité de générer une production qui soit intéressante.

Grammaire

À l’origine la notion de grammaire a été inventée par des linguistes pour définir les phrases syntaxiquement correctes des langues naturelles. On peut par exemple définir la grammaire du français qui indiquent les phrases syntaxiquement correctes du français ;

Exemple

« Le soleil a quatre pattes » est une phrase syntaxiquement correcte.
« soleil quatre a le pattes » est syntaxiquement incorrecte.

Mais cette phrase n'a pas de sens.

On ne s’occupe pas ici du sens de la phrase mais uniquement de sa structure grammaticale.

De la même manière on peut décrire les programmes syntaxiquement corrects d’un langage de programmation. On ne s’occupe pas ici du sens, ni de la terminaison, ni du bon fonctionnement du programme, mais juste de sa structure.

Exemple

int main(){ int x = 1/0 } est un programme C syntaxiquement correct.
mint aint)( 1/x = int 0{} n’est pas syntaxiquement correct.

On pourrait améliorer la grammaire pour indiquer/détecter qu'il ne faut jamais écrire 1/0.

On pourrait mais on compliquerait la grammaire et on ne réussirait pas à capter tous les cas de division par 0. Par exemple z=0; x=1/z; serait sans doute accepté. La détection de ce type d'erreurs n'est pas le rôle de la grammaire c'est celui d'autres étapes de la compilation (vérification de types, analyse statique de runtime errors).

Grammaire

Une grammaire \(G = (\Sigma, \mathcal{N}, germe, \mathcal{R})\) est définie par

\(\Sigma\), l'alphabet sur lequel sont écrit les mots du langage
\(\mathcal{N}\), l’alphabet des symboles non-terminaux utilisés pour définir les règles de la grammaire mais qui ne subsistent pas dans les mots du langage
\(S\in\mathcal{N}\), le germe de la grammaire (seed en anglais) : c'est le symbole non-terminal par lequel commence toute dérivation.
\(\mathcal{R}\), un ensemble de règles de réécriture de la forme
\(w \to w'\) où \(w\) et \(w'\) sont des productions ie. des mots de \((\Sigma\cup\mathcal{N})^*\) qui peuvent donc contenir des terminaux et des non-terminaux.

Exemples

La grammaire
\( G_1 = ( \Sigma =\{a\},~ \mathcal{N} = \{S\},~ germe = S,~ \mathcal{R} = \{~ S\xrightarrow{1} \epsilon,~ S\xrightarrow{2} a\mathop{\Large.} S ~\} ) \)
génère/reconnaît les mots du langage \(\mathcal{L}(a\ast)\), qui est régulier ie. reconnaissable par un AEF.
La grammaire
\( G_2 = ( \Sigma = \{a,b\},~ \mathcal{N} = \{S\},~ germe = S,~ \mathcal{R} = \{~ S\xrightarrow{1} \epsilon,~~ S\xrightarrow{2} a\mathop{\Large.} S \mathop{\Large.} b~\} ) \)
génère/reconnaît les mots du langage \(\{~a^nb^n \mid n\in\mathbb{N~\}}\), qui est algébrique ie. reconnaissable par une AUP.
La grammaire
\( G_3 = \left(\begin{array}{l} \Sigma = \{a,b\},~ \mathcal{N} = \{S\},~ germe = S,~ \\ \mathcal{R} = \left\{\begin{array}{l} S\xrightarrow{1} \epsilon, ~~~S\xrightarrow{2} a\mathop{\Large.} S \mathop{\Large.} b, \\ S\xrightarrow{3} b\mathop{\Large.} S \mathop{\Large.} a, ~~~S\xrightarrow{4} S \mathop{\Large.} S \end{array}\right\} \end{array}\right) \)
génère/reconnaît les mots du langage \(\{~ \omega \mid |\omega|_a=|\omega|_b~\}\), qui est algébrique ie. reconnaissable par une AUP.
La grammaire
\( G_4 = \left(\begin{array}{l} \Sigma = \{a,b\},~ \mathcal{N} = \{S,A,B\},~ germe = S,~ \\ \mathcal{R} = \left\{\begin{array}{l} S\xrightarrow{1} \epsilon, ~~S\xrightarrow{2} a \mathop{\Large.} B, ~~S\xrightarrow{3} b \mathop{\Large.} A, \\ A\xrightarrow{4} a \mathop{\Large.} S, ~~A\xrightarrow{5} b \mathop{\Large.} A \mathop{\Large.} A, \\ B\xrightarrow{6} b \mathop{\Large.} S, ~~B\xrightarrow{7} a \mathop{\Large.} B \mathop{\Large.} B \end{array}\right\} \end{array}\right) \)
génère/reconnaît le même langage que \(G_3\). Elle est plus difficile à comprendre que \(G_3\) mais a l'avantage d'être déterministe et de garantir la terminaison de l'analyse syntaxique.

Dérivation, Langage associé à une grammaire

Production versus Mot

On appelle production un séquence de symboles de \(\Sigma\cup\mathcal{N}\) ie. formée de terminaux et de non-terminaux, par exemple \(a\mathop{\Large.} S\mathop{\Large.} b\).
Un mot au sens habituel est en donc une production de \(\Sigma^*\).

Réécriture

La règle \(\omega\xrightarrow{r}\omega'\in\mathcal{R}\) d’une grammaire permet de réécrire la production \(\psi\) en \(\psi'\), si les productions \(\psi\) et \(\psi'\) peuvent se décomposer en trois parties : un début \(d\) et une fin \(f\) communes telles que
\(\psi = d.\omega.f\)
\(\psi' = d.\omega'.f\)
On écrit alors \(\psi \vdash_{r} \psi'\)

Dérivation

La grammaire \(G\) permet de dériver la production \(\psi'\) à partir de \(\psi\) s'il existe une séquence de règles \(r_1,...,r_k\) de \(\mathcal{R}\) qui transforme \(\psi\) en \(\psi'\) par réécritures successives
\( \psi \vdash_{r_1} \ldots \vdash_{r_k} \psi' \)
On écrit alors \(\psi \vdash_{\mathcal{R}}^* \psi'\).

Exemple

La grammaire \(G_2\) permet la dérivation suivante \(S \vdash_2 a\mathop{\Large.} S \mathop{\Large.} b \vdash_2 a\mathop{\Large.} a\mathop{\Large.} S\mathop{\Large.} b\mathop{\Large.} b \vdash_1 a\mathop{\Large.} a\mathop{\Large.} \epsilon\mathop{\Large.} b\mathop{\Large.} b\) donc \(S \vdash_{\mathcal{R}}^* a\mathop{\Large.} a\mathop{\Large.} \epsilon\mathop{\Large.} b\mathop{\Large.} b\)

Langage associé à une grammaire

La production d'une grammaire \(G=(\Sigma,\mathcal{N},germe,\mathcal{R})\) est l'ensemble des productions que l'on peut obtenir par dérivation \(\vdash^*_{\mathcal{R}}\) à partir du germe de la grammaire.
\( \mathcal{P}(G) = \{ \psi\in(\Sigma\cup\mathcal{N})^* \mid germe \vdash_{\mathcal{R}}^* \psi \} \)
Le langage d'une grammaire est l'ensemble des productions qui sont des mots, ie. qui appartiennent à \(\Sigma^*\).
\( \begin{array}{rcl} \mathcal{L}(G) &=& \mathcal{P}(G)\cap \Sigma^* \\ &=& \{ m\in\Sigma^* \mid germe \vdash_{\mathcal{R}}^* m \} \end{array} \)

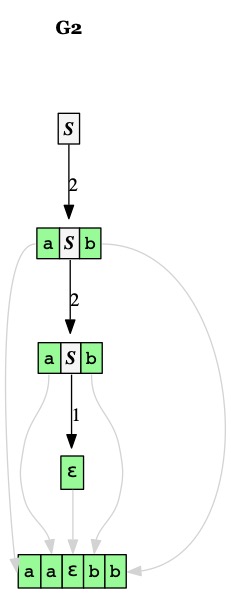
Un arbre de dérivation

Un arbre de dérivation est une représentation structurée de la séquence des dérivations depuis le germe de la grammaire. L'arbre indique par sa structure sur quel non-terminal est appliquée chaque règle.
La production d'un arbre de dérivation est la séquence de ses feuilles. Si cette production appartient à \(\Sigma^*\), on parle du mot de l'arbre

Représentation d'un arbre de dérivation

Voici deux représentations d'un même arbre de dérivation du mot \(aabb\) par la grammaire \(G_2\)

en version graphique avec le germe en haut et le mot généré en bas
le même en version tableau avec le germe en bas et le mot reconnu en haut

a
a
ε
b
b

a
a
ε
↑
1
S
b
↑
2
S
b
↑
2
S

Exemples d'arbre de dérivation

de la grammaire \(G_1\) [pdf]
de la grammaire \(G_2\) [pdf]
de la grammaire \(G_3\) [pdf].
Plusieurs dérivations de \(G_3\) conduisent au même mot : la grammaire est ambiguë, ie. non-déterministe.
de la grammaire \(G_4\) [pdf].
\(G_4\) est une version non-ambiguë équivalente à \(G_3\), au sens où elle reconnaît le même langage : \(\mathcal{L}(G_4)=\mathcal{L}(G_3)\).

Grammaires pour l'analyse syntaxique

Nous avons présenté la notion de grammaire sous l'angle des dérivations possibles. L'usage de grammaires génératives est limité à la production automatique de littérature, musique et de séquences de tests.

L'usage le plus courant des grammaires est la reconnaissance de format de données appelée analyse syntaxique (parsing en anglais).

Toutes les grammaires ne permettent pas de générer un analyseur syntaxique (parseur en anglais).

Pour qu'une grammaire permette une analyse syntaxique il faut qu'elle respecte deux critères

La garantie de terminaison de l'analyse syntaxique obtenue par l'élimination de la récursivité gauche
Le déterminisme obtenu par élimination des ambiguités

Nous allons étudier les techniques d'élimination de la récursivité gauche et des ambiguités à travers les exercices.

Classification des grammaires

Des parseurs qui calculent

Les transparents du cours (en anglais) [pdf]
Travaux pratiques en Java + Javacc sur le dépôt [git]

Le projet

Traducteur AEF vers DOT

L'objectif du projet est de produire la représentation graphique d'un automate au format .dot pour l'outil graphviz

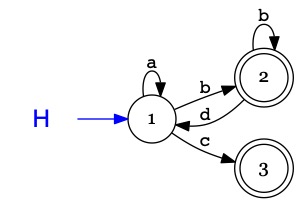
à partir de la description AEF de l'automate

AEF(H){ ->1 -a-> 1 -b-> (2) -b-> (2) -d-> 1 -c-> (3) ; }

Vous serez guidés

Nous étudierons en cours et en TP plusieurs exemples pour illustrer chaque difficulté du parsing.
Ensuite nous traiterons une partie du projet en cours.
Vous aurez à finir l'implantation en vous appuyant sur les connaissances acquises en cours et en TP.

Projet collaboratif

Le projet est à réaliser par groupe de 6 de provenances différentes.
Vous devez tous maîtriser ce développement car il y aura des questions à l'examen sur le projet.
L'objectif n'est pas seulement la note. L'objectif c'est d'apprendre et de maîtriser la technique de parsing/traduction.

Comment collaborer ?

Prévoyez des étapes dans le projet
1. installez graphviz pour pouvoir tester
2. produire avec java un fichier dot : digraph aef{ test; }
3. parser "AEF(A){}" et produire un fichier dot : digraph aef{ A; }
4. parser "AEF(A){ ->1 ; }" et produire un fichier dot : digraph aef{ A -> 1 [color=blue]; }
5. parser "AEF(A){ ->1 -a-> 2 ; }" et produire un fichier dot : digraph aef{ A -> 1 [color=blue]; 1 -> 2 [label="a"]; }
6. ...
Vous devez coder chacun le projet. Pour autant, discutez régulièrement entre vous.
1. pour mettre en commun les idées
2. pour échanger sur les points délicats
3. pour ne pas rester bloquer
4. pour faire le point sur l'avancement et pour vous repartir des tâches
5. pour fusionner le code
Au final vous devez
1. fournir un seul code pour le groupe
2. tous maîtriser ce code.
Vous aurez ainsi appris, techniquement, à écrire des parseurs/traducteurs et, humainement, à coder en équipe.

Rendu de projet

Il faut rendre au plus tard le VENDREDI 22 JANVIER un fichier .zip contenant votre répertoire Projet/

sans les répertoires ast/ et dot/
dans le src/aef_to_dot/, le parser .jj et les classes Java Dot.java, Transition.java, Aef.java mais pas les classes générées par JavaCC
dans le répertoire aef, des fichiers de tests pertinents au format .aef que votre parseur accepte.

Plusieurs niveaux d'investissements et la note associée

[10,12] : parser AEF et sortie dot
[12,14] : + état (primés)* + dernier ";" optionnel
- On doit accepter les états \(1, 1', 1'', 1''', ...\)
- On doit accepter AEF(A){->1;} et AEF(A){->1}
[14,16] : + couples (de couples)* d'états /!\ au non-déterminisme>
- On doit accepter les états de la forme (1,(2',3'')) issus du produit de trois automates \(A \times (A' \times A'')\)
- Attention au cas \(((1,2))\) d'un état accepteur formé d'un couple d'états
[16,18] : + détection des états inaccessibles affichés en gris clair
L'algorithme de détection des états inaccessibles consiste à parcourir le graphe de l'automate depuis les états initiaux et à marquer les états rencontrés.
- Au départ les états à explorer sont les états initiaux
- on marque les états à explorer comme accessibles, on suit les transitions sortant des états à explorer, les cibles de ces transitions deviennent les nouveaux états à explorer.
- Le parcours s'arrête lorsque les nouveaux états à explorer sont déjà marqués comme accessibles.
- Les états non-marqués à l'issue de ce parcours sont inaccessibles.
[18,20] : + détection des états puits affichés en noir
C'est le même algorithme de parcours de graphe avec marquage mais cette fois on part des états accepteurs et on parcourt les transitions de l'automate en sens inverse.

À l'issue des TP sur les parseurs, le projet devrait vous prendre 4 × (1h30, le temps que j'ai mis pour viser 14/20) = 6h.

Fournitures

Les fichiers nécessaires au projet sont sur le dépôt [git]

Il contient

un parser aef_parser.jj rudimentaire qui parse correctement AEF(A0){} (à compléter)
des classes java Dot.java, Transition.java, Aef.java (à compléter)
des exemples d'automates au format AEF
des fichiers DOT produits par mon traducteur : aef01.dot est un exemple de ce que vous devez produire pour l'automate aef01.aef.

Pour vous aider à concevoir votre grammaire, je fournis également, pour chaque exemple, au format [pdf],
les arbres (simplifiés) de reconnaissance/dérivation produit par mon parseur lors de la traduction.
Ça ne vous est pas demandé dans le projet !

Conception d'une grammaire

Dans ce cours nous allons voir comment concevoir la grammaire qui reconnaît la notation AEF utilisé dans ce cours.

Comment naît une notation ?

En rédigeant ce cours j'ai constaté qu'il n'y avait pas de notation lisible, simple et compacte pour les AEF. J'ai donc inventé ma propre notation par déformation professionnelle.

Les étapes de conception d'un traducteur

Lorsqu'une notation (AEF) n'est pas acceptée par les outils existants (graphviz dans notre cas) il faut concevoir un traducteur de la nouvelle notation vers le format d'entrée des outils : \(AEF \to DOT\) en ce qui nous concerne.

La première étape consiste à définir la grammaire de la nouvelle notation \(AEF\) (cette leçon).
Ensuite on implante la grammaire dans un générateur de parseur (le TP à venir). On est alors capable de lire et reconnaître le format \(AEF\).
On ajoute au parseur des instructions qui calculent/construisent le résultat de la traduction au format \(DOT\) (le projet).

Analyse d'un exemple caractéristique

Pour concevoir une grammaire on commence par écrire un ou des exemples qui illustre les possibilités cas de la nouvelle notation. J'ai rassemblé les différents cas dans un seul exemple :

  AEF(A){ ->1 -a->2 -b->1 ; ->2 -a->(3) ; 3-a,b->3 ; }

On analyse l'exemple pour y trouver des régularités.

  AEF(
  A
  ){
   -> 1  -a->  2    -b->  1  ; 
   -> 2  -a->  (3)  ; 
   3     -a,b->  3  ; 
   } 

AEF(

Ident

){

Start

Arrow

Target

Arrow

Target

;

Start

Arrow

Target

;

Start

Arrow

Target

;

}

AEF(

Ident

){

Start

Step

;

Start

Step

;

Start

Step

;

}

AEF(

Ident

){

Path

}

La descrition d'un automate commence par AEF{ et se termine par }.
L'automate est constiuté d'un certain nombre de chemins, \(Path\).
Un automate a forcément un état donc on interdit le cas "AEF{}" en imposant au moins un chemin.
Un chemin est constitué d'un point de départ, \(Start\), suivi de 0 ou plusieurs \(Steps\) et terminé par un ponit-virgule
Le point de départ, \(Start\) peut-être un état initial ou non. La flêche -> qui le précède est donc optionnelle.
Un pas, \(Step\) est consituté d'un flêche, \(Arrow\), qui porte un ou plusieurs symboles séparés par des virgules et d'une cible \(Target\).
Une cible est un état accepteur ou neutre, mais pas un état initial : on ne propose pas la notation 1 -a-> ->2 qui serait confuse. La grammaire doit donc faire la distinction entre les cas \(Start\) et \(Target\).

Proposition de grammaire

\( \begin{array}{rcl} Aef &::=& \texttt{"AEF("} \cdot Ident \cdot \texttt{")\{"} \cdot (Path)^+ \cdot \texttt{"\}"} \\ Path &::=& Start \cdot (Step)^* \cdot \texttt{";"} \\ Start &::=& (\texttt{"->"})^? \cdot Target \\ Accepting &::=& \texttt{"("} \cdot State \cdot \texttt{")"} \\ State &::=& Ident \\ Step &::=& Arrow \cdot Target \\ Arrow &::=& \texttt{"-"} \cdot SepSymbols \cdot \texttt{"->"} \\ SepSymbols &::=& Symbol \cdot (\texttt{","} \cdot Symbol)^* \\ Symbol &::=& \texttt{"a"} \mid \ldots \mid \texttt{"z"} \\ Target &::=& Accepting \mid State \end{array} \)

Puisque les états sont des identificateurs, pourquoi créer un non-terminal \(State\) alors qu'on aurait pu simplement écrire \(Ident\) ?

Il est vrai que les états sont actuellement des identificateurs, mais ça pourrait évoluer. On pourrait étendre la notion d'états afin de reconnaître d'autre notations utilisées dans le cours telles que \(1'\), \((1,2)\), \(\{1,3\}\). Le fait d'utiliser un non-terminal \(State\) prépare l'évolution de la grammaire. Si on a besoin d'étendre la reconnaissance des états il suffira de changer la ligne qui définit \(State\) sans avoir à toucher au reste de la grammaire. En exercice nous ajouterons la possibilité d'écrire des états « primés » ie. suivis de \('\).

Élimination des expressions régulières

Les outils d'analyse lexicale (Lexer) autorisent les expressions régulières \((.)?\), \((.)+\), \((.)\ast\). Certains outils d'analyse syntaxique (Parser) l'autorisent dans la grammaire. et nous en avons fait usage. Elles sont pratiques mais pas indispensables. D'autres outils ne l'autorisent pas et au final tous les outils éliminent les expressions régulières en donnant une traduction sous forme de règles de grammaires. Mais surtout, l'élimination des expressions régulières est nécessaire avant de compléter le parser avec des calculs.

Non-terminal optionnel
\((NT)?\) est remplacé par \(NTo\) (pour optional) et on ajoute la règle \(NTo ::= NT \mid \epsilon\)
Itération de Kleene
\((NT)\ast\) est remplacé par \(NTs\) (pour star) et on ajoute la règle \(NTs ::= NT \cdot NTs \mid \epsilon\)
Au moins une fois
\((NT)+\) est remplacé par \(NTp\) (pour plus) et on ajoute la règle \(NTp ::= NT \cdot NTs\) et la règle \(NTs\) précédente.

Alternative

\(e \cdot ( NT1 \mid NT2 )\) est remplacée par \(e \cdot A\_NT1\_NT2\) (pour alternative) et on ajoute la règle \(A\_NT1\_NT2 ::= NT1 \mid NT2\)

La forme \((e \cdot NT1) \mid (e\cdot NT2)\) qui est équivalente contient un non-déterminisme qui ne convient pas au parseur puisqu'il doit choisir entre les deux alternatives au moment de reconnaître \(e\). L'ajout d'une règle repousse le moment du choix après la reconnaissance de \(e\) ; à ce moment là le parseur aura lu un autre caractère qui lui permettra de choisir entre les alternatives \(NT1\) et \(NT2\).

Extensions de la grammaire

Exercice 1

Modifiez la grammaire pour autoriser les états primés.

Exercice 2

Modifiez la grammaire pour autoriser l'absence de point-virgule ";" au dernier chemin avant "}" et permettre à l'utilisateur d'écrire AEF(A){ ->1 } au lieu d'exiger AEF(A){ ->1 ; }

Exercice 3

Modifiez la grammaire pour autoriser les couples (de couples)* d'états.

On doit accepter les états de la forme (1,(2',3'')) issus du produit de trois automates \(A \times (A' \times A'')\)
Attention au cas \(((1,2))\) d'un état accepteur formé d'un couple d'états

Vous aurez besoin de créer plusieurs non-terminaux pour distinguer les étapes dans la reconnaissance d'un état : au moins begin_state, end_state