Figure 1: Invariant verification of SPL programs
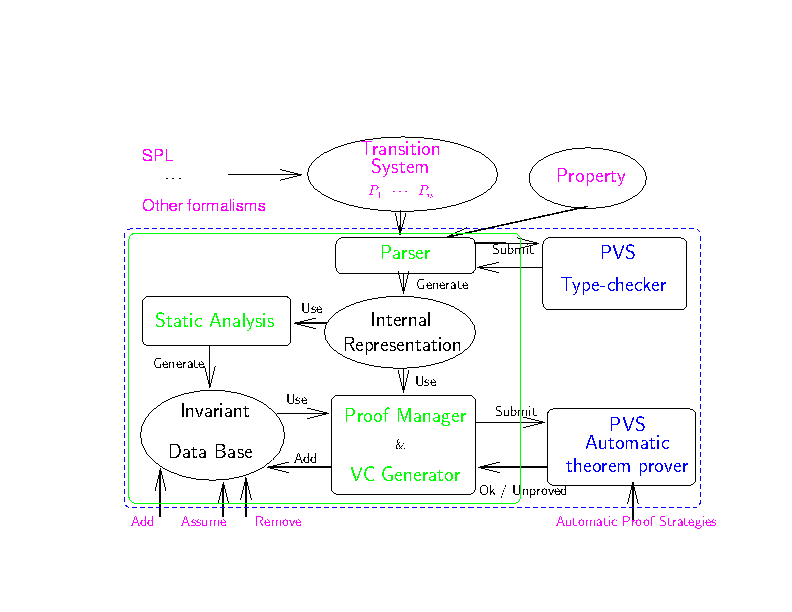
Figure 2: Abstraction and refinement with the abstractor
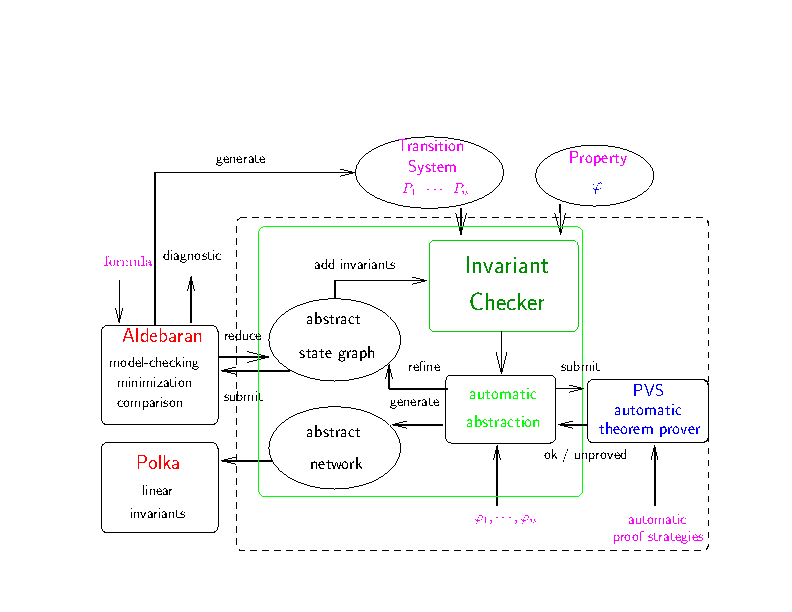
In the Abstractor, we approximate the most general abstraction in two ways.
(a) As already, stated, we take a safe over approximation, that is if it cannot be proven that two abstract states are
unrelated, then they are related. This is common to all tools using the principle of predicate abstraction.
(b) We consider not any two individual pair of abstract states individually. We compute only successors of reachable states, and consider as potential successor sets only monimials, that is we check the value of the abstract
successor set predicate by predicate.
(c) On the other hand, we reduce the overapproximation
by using a number of optimisations exploiting "easily computable facts" in order to reduce the set of reachable states and of potential successors of a given state.
Most of the successor tools of our Abstractor have chosen different heuristics for efficiently computing abstractions. Most of them, exploit optimisations close to those of (c), but most of them consider abstractions where concrete variables are abstracted individually, that is abstract predicates are built from literals involving only one variable. We do not require such a restriction as our initial aim was, given some system consisting of a set of parallel processes, to constract an abstraction of the global control graph, in order to obtain better results with the Checker (the better the control approximation, the more invariants are inductive invariants, which are those detected by the checker). The obtained abstract state graph can also be analyzed directly by the Aldebaran tool using state exploration of state graphs (note that today Aldebaran is distributed as a module within CADP or IF).
Abstraction refinement is done starting from a minimization obtained using the Aldebaran tool but is not fully automatized.

