The Argos Compiler - Documentation

Argos

The compiler implements all elements of the Argos[1] language. This document is not meant to be an introduction to Argos, but a documentation of the compiler's features and syntax. Please see [1] if you are looking for an introduction to Argos.

Simple Example

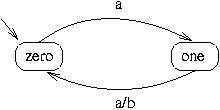
The code below describes the automaton to its right, a simple modulo-2 counter that emits an b every two a.

main simple(a)(b)

process simple(ia)(ib){
    controller{
      init zero

      zero {}
      -> one with ia;

      one {}
      -> zero with ia/ib;
    }
}

Argos programs consist of a collection of processes, which represent automata. In our example we have only one process called simple. It starts with the keyword process, followed by its name, simple, a list of its inputs, here only ia and a list of its outputs, here ib. The input and output variables scope over the body of the process, which follows between braces.

Here, the body contains a flat automaton. This is specified by the keyword controller. Between the following braces, we first specify the initial state (init zero), then follows a list of states with their transitions. Each state of the automaton is specified by its name (here zero and one). It can be refined between the following braces. After the braces follows a list of transitions for each state. Each transition starts with -> and ends with a semicolon. Between them are the state to which the transition goes, the keyword with and the activation condition. If the transition has outputs, they follow after a slash after the condition.

The line main simple(a)(b) specifies which process is the top level automaton of the program, and names its parameters.

Parallel Product and Encapsulation

The automaton below is a simple example of Argos' instantaneous dialogue. When the inputs a and c are true, the left automaton emits b and the right automaton receives b and emits o. All this happens at the same instant.

main instantaneousDialogue(a)(o)

process instantaneousDialogue(a)(o){ 
  internal b{ 
    controller{  
      init A
      A{}
      -> B with a&c/b;
      B{}
    }
    ||
    controller{
      init C
      C {}
      -> D with b/o;
      D{}
    }
  }
}

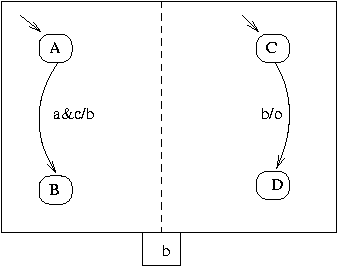In the body of the process instantaneousDialogue two automata are put into parallel and the communication signal b is encapsulated. The outermost element, the encapsulation of b, is expressed by internal b. b can be used as an input or an output between the following braces. To express the parallel composition, we put the parallel operator || between two automata.

The encapsulation can be modified by putting the keyword exported after internal. Then, the encapsulated signals will stay output signals after the encapsulation has been applied. In the above example, declaring b exported will mean that it is emitted together with o.

Note that we express the logical and as &. The logical or is written as |, and the logical not is a prefixed ~. Parentheses can also be used to write an expression.

Refinement

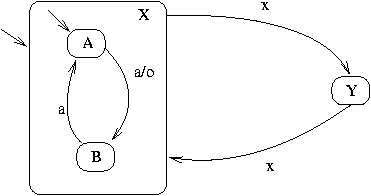
In the example below, the automaton counts the as while it is in state X. When it quits state X and comes back later, it restarts counting in the initial state A.

main R (a, x)(o)

process R (a, x) (o){
  controller{
    init X
    X{
       controller{
         init A
         A {}
         -> B with a;
         B {}
         -> A with a/o;
       }
    }
    ->Y  with x;

    Y{}
    -> X with x;
  }
}

Inhibition

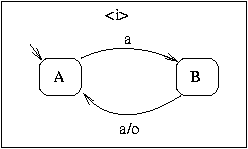
Note that the compiler has not a whennot-operator, but a when-operator. The program below only counts an a when i is present at the same time.

main inhibit(a,i)(o)

process inhibit(a,i)(o){
  when (i){
    controller{
      init A
      A {}
      -> B with a;
      B {}
      -> A with a/o;
    }
  }
}

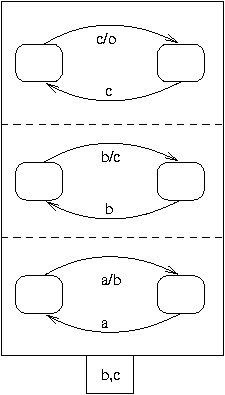
Process Calls

Processes can call other processes. In the example below, we instantiate a one-bit counter three times to obtain a three-bit counter.

main modulo8counter(a)(o)

process modulo8counter(a)(o){
  internal b,c{
    modulo2counter(a)(b)
    ||
    modulo2counter(b)(c)
    ||
    modulo2counter(c)(o)
 }

process modulo2counter(i)(o){
  controller{
    init A
    A {}
    -> B with i;
    B {}
    -> A with i/o;
  }
}

Integer Variables

The ArgosCompiler also has a limited support for integer variables. In a process declaration, integer variables can be declared in three different ways:

as input variables, declared after the boolean inputs, and each variable preceded by the keyword int,
as output variables, declared after the boolean outputs, and each variable preceded by the keyword int , and
as internal variables, declared before the initial state declaration, with the syntax int varName = initialValue;.

The int keyword must also precede integer variables in process calls. In the main process call, output variables are also assigned their initial values: they are followed by an = and an initial value. Output and internal integer variables can be assigned values by transitions, where assignments of the form varName=intExpression can be placed among the outputs. intExpression are either integer constants, integer variables, integer variables preceded by the keyword pre (referring to the value of the variable at the previous instant), or two intExpressions combined by one of the operators +, -, or *.

Integer variables can be used in the assignments of the conditions using the syntax intExpression <intExpression or intExpression >intExpression.

Here is an example for a Argos program with integer variables. When in state on, it emits the value of its internal counter variable value. value is increased by input variable a while value is smaller then 10, otherwise is it decreased by a.

main counter(b, int a)(int o = 0)

process counter(b, int a)(int o){
    controller{    

      int value = 0;
    
      init Off
            
      Off{}
      -> On with b/ o = value;
            
      On {}
      -> Off with b / o = 0;
      -> On with  ~b & pre value < 10/ o = value, value = pre value + a;
      -> On with  ~b & pre value > 9 / o = value, value = pre value - a;
    }
}

Note that determining if a state is complete and deterministic is much harder with integer variables. The ArgosCompiler takes a conservative approach, and rejects all programs for which it cannot verify that they are deterministic and complete. Therefore, if you have a transition with condition a < b + 3, you must add ~ a < b + 3 to the conditions of all other transitions of the state. However, if you only use expressions of the form var (<|>) const, the ArgosCompiler should correctly determine determinism and completeness.

Parallel processes must never have common integer output variables. This means an integer variable is always assigned a value by exactly one process. Therefore, Integer variables cannot be encapsulated.

File Inclusion

The ArgosCompiler disposes of a primitive mechanism to include process and aspect declarations form other files into one file. Therefore, insert

 include pathToFile1, ..., pathToFilen;

at the beginning of the an Argos file. The path are resolved from directory where the ArgosCompiler is executed. If the compiler cannot find an included file, it prints an error message and gives the current directory.

Larissa

Larissa is an aspect language for Argos, and consists of an join point selection mechanism and two different sorts of advice, toInit advice and recovery advice. [2] is detailed introduction to Larissa. However, the compiler now uses a better join point model, which is described in [3], along with a shorter introduction to Argos and Larissa.

Aspects are entities that contain a pointcut and an advice. They are applied to program by an aspectCall, an operator which takes an Argos program and an aspect as argument. The aspect is then applied to the program. An aspect call can occur inside a process, after an automaton. It starts with <| followed by the name of the aspect, a list of the aspect's inputs and a list of its outputs, each of these between parentheses. E.g., the following code

exampleProcess(a)(b,o) <| simpleAspect(a,b)(o,p)

applies the aspect simpleAspect to the process call exampleProcess. Note that the aspect can use outputs of the automaton to which it is applied as inputs.

Pointcuts

Pointcuts choose the transitions we want to modify from an existing automaton, called the base program. To select those transitions, the programmer provides an automaton, the pointcut, with a special output JP. Conceptually, a transition in the base program is selected, when, during the parallel execution of the base program and the join point, JP is emitted. Technically, we perform a parallel product between the base program and the pointcut, and select all those transitions as join points which emit JP.

toInit Aspects

toInit aspects add transitions to the join points, which go to certain states of the program. These states are specified by a finite trace on the inputs. When the woven program executes a join point, the aspect ensures that the program does not continue its execution, but goes to the state specified by the trace.

This is an example for a toInit aspect:

toInit exampleAspect(a,b,c)(d) {
  joinpoint jp;
  pointcut PC(a,b)(jp);
  adviceOutputs d;
  trace init(a&~b&~c.a&b&c);
}

toInit specifies that this is a toInit aspect, followed by the name of the aspect, exampleAspect. Then follows the inputs of the aspect and the outputs of the aspect. In the body of the aspect, joinpoint specifies the output JP of the automaton, which specifies the states where the aspect can be applied, here jp. After pointcut follows a process call, referring the pointcut. The outputs must contain the join point variable specified above. The keyword adviceOutputs is followed by a list of outputs that are added to the advice transitions. This line is optional. The line trace init(a&~b&~c&.a&b&c); gives the traces that specifies the final point of the added transition. After the keyword trace follows either init, this, or target. The trace is then executed respectively from the initial state of the automaton, the initial state of the current join point transition, or the target state of current the join point transition. The actual trace follows between parentheses. It must span over all input variables of the program the aspect is applied to and of the pointcut. The variables of one element of the trace are separated by an &, and the elements are separated by a dot. The trace in the example spans over the variables a, b and c and has a length of two.

Recovery Aspects

Recovery aspects allow the programmer to jump back in the execution trace, to a state that has previously been passed. A recovery aspect marks some states of the program as recovery states. When the program passes a join point during execution, it goes back to the last recovery state it has passed. Recovery states are selected by a recovery automaton with a special output REC. Again, we calculate the product between the base program and the recovery automaton, but we select all states that have an outgoing transition which emits REC.

This is an example for an Recovery aspect:

recovery  restartProd(a,b,c)(act)(){
	joinpoint JP;
	pointcut PointCut(a,b)(JP);
	recSig REC;
	recAut RecoveryStates(b,c)(REC);
}

recAut refers to the recovery automaton, the automaton that specifies the recovery states. The recSig is the marker signal for the recovery states in recAut, it must be a output of recAut.

Inserting Advice Automata

Instead of inserting a transition to target state, Larissa can insert complete automata between a join point and a target state. Currently, this is only possible for toInit automata. The programmer must insert a line like the following before the specification of the trace.

	insert inserted(advice,a)(back);

insert is a key word indicating that an automaton should be inserted, inserted(advice,a)(back) is a process call to the automaton that is inserted. advice and back are special signals that must not be defined in the aspect. The process inserted should do nothing until it receives its input advice, then execute whatever should be executed as advice and eventually emit back and do nothing until it receives again advice. The weaving will then introduce a waiting state between the source state of the join point transition and the target state. The advice transition then goes the waiting state and emit advice, and there is a transition from the waiting state to the target state with condition back. The inserted automaton is then put in parallel with the woven program and advice and back are encapsulated. Thus, when a join point of an aspect with an inserted automaton is reached, the woven program goes to the state to which the transition labeled by advice points, executes the inserted automaton until back is emitted, and then resumes the execution of the woven program at the target state of the aspect.

[1] F. Maraninchi and Y. Rémond. Argos: an Automaton-Based Synchronous Language. Computer Languages no 27(1/3):61-92, Elsevier pub., 2001.

[2] K. Altisen, F. Maraninchi and D. Stauch. Aspect-oriented programming for reactive systems: Larissa, a Proposal in the synchronous framework. in Science of Computer Programming, Special Issue on Foundations of Aspect-Oriented Programming, 2006.

[3] K. Altisen, F. Maraninchi and D. Stauch. Modular Design of Man-Machine Interfaces with Larissa. 5th International Symposium on Software Composition, in Conjunction with ETAPS 2006, Vienna, Austria. To Appear.